Optical resonant cavities have attracted a great deal of attention because of their ability to manipulate optical energy in small volume and to consequently tailor light-matter interactions. This ability is of great importance, for it facilitates useful practical applications in designing optical filters, switches, low-threshold lasers, brighter single-photon sources, and so on.^[1–9] Moreover, both confining the light in high-Q cavities to increase the lifetime of the optical excitation and reducing the effective mode volume (V_eff) are crucial in the designs of the optical resonant cavities.^[10]

Surface plasmon (SP) is the collective electron charge oscillations that exist at the interface between the metal and dielectric media. It is capable of producing highly enhanced optical fields below the diffraction limit, which yields great potential to confine and manipulate light at sub-wavelength scale with a reduced V_eff.^[11] As a result, recently, plasmonic resonators have been presented widely in theory and experiment, including diverse metallic nanocavities making use of localized SP (LSP)^[12–15] and surface plasmon polaritons (SPPs).^[10,16] However, the Q factors of LSP resonators are limited because of radiation and metallic losses. Although the SPPs resonators exhibit higher Q factors compared to LSP resonators, the former also suffer from huge propagation loss. In order to reduce propagation loss while offering tight mode confinement at sub-wavelength scale, a hybrid plasmonic waveguide comprised of a high-index dielectric nanowire separated from a silver surface by a nanoscale low-index dielectric gap was proposed,^[17] which appears to be helpful in improving the Q factors of SPPs resonators. Subsequently, a plasmon laser^[18] based on this kind of hybrid plasmonic waveguide was successfully demonstrated, and the feedback mechanism of this nanometer-scale plasmonic laser is based on a Fabry–Perot cavity provided by reflection of the nanowire end-facets. Taking into account the low reflection of the nanowire end-facets, we hope to further improve the Q factors of cavities by introducing high-reflectivity DBRs,^[10,16] while maintaining a small mode volume.

In this letter, we design a hybrid plasmonic nanocavity based on DBRs, with an ultra-small mode volume and a high Q factor. As an example, Purcell factor of up to nearly 20000 and low gain threshold are achieved at 1550 nm, which are preferred to enable highly efficient nanocavity feedback for the potential applications such as deep sub-wavelength scale lasing.

The proposed hybrid plasmonic nanocavity, as shown in Fig. 1(a), consists of a high-index GaAs nanowire separated from a Ag surface possessing shallow periodic gratings by a very thin low-index SiO₂ dielectric layer. The background is also made out of SiO₂ dielectric materials. The shallow periodic gratings serve as high-reflection DBRs, and two identical DBRs are placed along the direction of the GaAs nanowire with a selective distance between them to define a Fabry–Perot nanocavity, of which the length is L₁. The lengths between the cavity edge and its adjacent DBRs are defined as L₂, as shown in Fig. 1(a). The properties of this hybrid plasmonic nanocavity are investigated using COMSOL Multiphysics, a commercial finite-element-method-based software package. In our numerical simulations, the dielectric property of Ag is taken from Johnson & Christy^[19] and the permittivities of GaAs and SiO₂ are set to be 12.25 and 2.25.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) Schematic diagram of the hybrid plasmonic nanocavity, which comprises a high-index semiconductor nanowire separated from a patterned metal substrate by a nanoscale low-index dielectric gap. (b) Dependence of the real part of the effective refractive indices on the incident wavelength. The insets are the normalized electric field distributions in the yz plane corresponding to the two grating sub-period regions.

By controlling the hybridization of the fundamental guided mode of the 100 nm radius GaAs nanowire and the SPPs of the dielectric–metal interface at the telecommunication wavelength 1550 nm, we can simultaneously make sure tight mode confinement and single-mode propagation, as the dielectric gap width between the nanowire and the upper metal plane is set to g₁ = 2 nm. The depth of the grooves are set as h = 25 nm, in other words, g₂ = g₁ + h = 27 nm. The center wavelength of the stop band is related to the mode effective refractive indices. The mode effective refractive indices are calculated and displayed graphically in Fig. 1(b). It shows the real part of the effective refractive indices of the guided-mode propagating in the gap region between the GaAs cylinder and the metal surface with patterned grooves as a function of incident wavelength. Here, n_eff1 and n_eff2 are the effective refractive indices of the two-grating sub-period regions with gap widths of g₁ = 2 nm and g₂ = 27 nm, respectively. The normalized electric field intensity distributions of the hybrid plasmonic mode in the yz plane are shown in the insets of Fig. 1(b), corresponding to these two-gap widths, which clearly show that the hybrid plasmonic mode can be strongly confined in the gap region. In order to make sure the stop band is around 1550 nm, the grating period is designed to P = 400 nm and the width of the grooves are assumed as P/2 for simplicity.

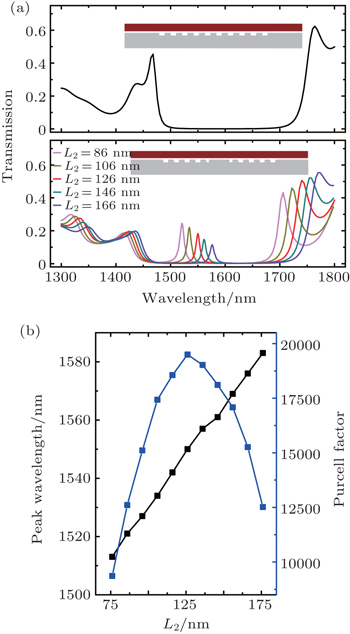
The optical properties of the hybrid plasmonic nanocavities are subsequently investigated. In order to evaluate the propagation performance of the DBR, the transmission of a DBR grating composed of 10 periods with periodicity P = 400 nm is simulated as plotted in the upper panel of Fig. 2(a). The incoming hybrid plasmonic mode tightly confined in the gap region between the patterned metal surface and nano-cylinder is reflected with > 99% efficiency, thus forming a stop band with a bandwidth of 200 nm, ranging from 1500 nm to 1700 nm, which actually can be tuned by varying the grating period. A hybrid plasmonic nanocavity with length L₁ = 770 nm can be constructed by placing two identical 5-period DBRs together for the defect state located around 1550 nm. The transmission spectra of the hybrid plasmonic nanocavities with different L₂ (the lengths between the cavity and its adjacent DBRs) are presented in the bottom panel of Fig. 2(a), in which there exist sharp resonant peaks located inside the stop band, and as L₂ increases, the resonant peaks red-shift obviously. In principle, a high-performance nanocavity can be scaled over a broad wavelength range for the target wavelength by optimizing the geometry of the nanostructure such as the parameters L₁ and L₂.

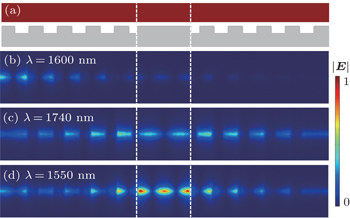
For example, when L₂ = 126 nm, a hybrid plasmonic nanocavity with resonant wavelength at 1550 nm can be achieved. Here, we use the ratio of the center wavelength of the resonant peak (λ_c) and its full width at half maximum (FWHM) to define the Q factor of this hybrid plasmonic cavity mode (Q = λ_c/FWHM). In this case, the transmittance of sharp resonant is 18.3% at λ_c = 1550 nm and the corresponding FWHM is 8.3 nm, which leads to a high Q factor of 187 owing to the low propagation loss. Since the transmission and FWHM of the resonant peak in the hybrid plasmonic nanocavity depend upon the period number (N) of the DBRs, as N increases, the FWHM reduces accordingly.^[20,21] As an example, when the N of each DBR is 7 and 10, the FWHM reduces to about 5.3 and 4.6 nm, yielding higher Q factors of up to 292 and 337, respectively. However, as N increases, the decrease of transmittance of the resonant peak will strongly limit the detection and its further application.^[20,21] On the other hand, the mode volume of the proposed nanocavity can be calculated by

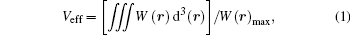
When L₂ = 126 nm, an ultra-small mode volume of 3.04 × 10⁻²² m³ can be achieved for the hybrid plasmonic nanocavity with length L₁ = 770 nm.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Transmission spectrum of a 10-period DBR (upper panel) and transmission spectra of hybrid plasmonic nanocavity composed of two 5-period DBRs with different L2 (bottom panel). Insets are the schematics of each structure. (b) Dependence of the wavelength of the resonant peak and Purcell factor on the length L2, varied from 76 nm to 176 nm at a step of 10 nm (L1 = 770 nm).

Based on an overall consideration of the effect of Q factor and V_eff on the nanocavity, the Purcell factor is introduced to characterize the performance of the proposed nanocavity. Moreover, the Purcell factor is also a figure of merit to represent the ability of a cavity for spontaneous emission enhancement, which is described as^[22]

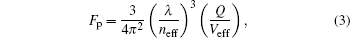
To illustrate the mode profile of the DBRs-based nanocavity clearly, the simulated normalized electric field intensity of the nanocavity in the xy plane at different wavelengths are plotted in Fig. 3. Here, for the proposed sample L₂ = 126 nm, the hybrid plasmonic mode propagating characteristics for wavelengths at 1600 nm, 1740 nm, and 1550 nm are presented, which correspond to three typical wavelengths including inside the stop band, outside the stop band, and on resonance, due to the excitation of cavity mode, respectively. As shown in Fig. 3(b) at wavelength λ = 1600 nm, we observe that the light is reflected after a couple of periods inside the stop band. Moreover, the light propagates through the structure at wavelengths outside the stop band, as shown in Fig. 3(c), when the wavelength is at 1740 nm. Figure 3(d) shows that at λ = 1550 nm, the incident light couples and strongly resonances in the nanocavity.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. (a) Schematic diagram of the hybrid plasmonic nanocavity. Simulated normalized electric field intensity from the xy plane at the middle of the dielectric gap of hybrid plasmonic nanocavities at (b) λ = 1600 nm (inside the stop band), (c) λ = 1740 nm (outside the stopband), and (d) λ = 1550 nm (on resonance).

Due to the large Purcell factor, which represents the fine ability of the hybrid plasmonic nanocavity for spontaneous emission enhancement that was demonstrated in plasmonic nanoparticle antennas,^[23] we also demonstrate the utility of the hybrid plasmonic nanocavity to control emission properties of dipole for the optimized L₂ = 176 nm at wavelength of 1550 nm. Figure 4(a) shows simulated photoluminescence (PL) intensity spectra of x-, y-, and z-polarized dipole sources being placed at the center of our proposed DBRs-based hybrid plasmonic nanocavity. The PL intensity of z-polarized dipole source coupled to the cavity is much higher than that of x- and y-polarized one. This is because E_z is about three orders of magnitude higher than E_x and E_y at this point. The resonance peak of PL intensity spectrum of z-polarized dipole λ is 1550 nm, which corresponds well with transmission spectra of the cavity. Figures 4(b)–4(d) show E_x, E_y, and E_z distributions in the yz plane of the cavity without dipole at λ = 1550 nm, respectively. The electric field distributions also reveal that E_z is much higher than E_x and E_y.

Considering the relatively high Q factor and ultra-small mode volume of the hybrid plasmonic nanocavity, we expect a low gain threshold for the lasing applications. To find out the gain threshold, a nanowire is chosen to be doped with optical gain material and we set the complex permittivity of the GaAs as . We then calculate the absorption efficiency for the hybrid plasmonic nanocavity with different gain coefficient . The zero absorption at a critical value, i.e., the gain threshold, means that loss in metal has been totally compensated by the gain in the nanowire. As a result, the gain threshold α_th for the hybrid plasmonic nanocavity with L₂ = 126 nm is calculated to be 266 cm⁻¹, much smaller than that of the recently reported plasmonic lasing structures.^[22,24]

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Simulated PL intensity spectra for x- (black line), y- (blue line), and z-polarized (red line) dipole sources placed at the center of cavity with L2 = 126 nm. (b)–(d) Ex, Ey and Ez distributions in the yz plane of the cavity without dipole at the center of the cavity respectively.

We design a hybrid plasmonic nanocavity with high Q factor and ultra-small mode volume based on the DBRs and the hybrid plasmonic waveguide. The characteristics of Purcell factor of up to nearly 20000 and low gain threshold approaching 266 cm⁻¹ at the telecommunication wavelength 1550 nm provide efficient cavity feedback and high lasing efficiency. This result shows significant potential for sub-wavelength lasing applications and development of nanoscale integrated photonic circuits