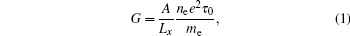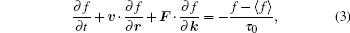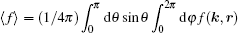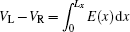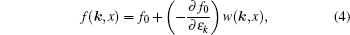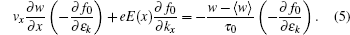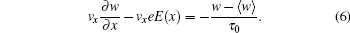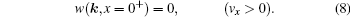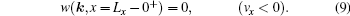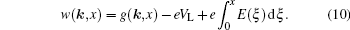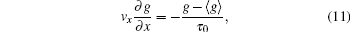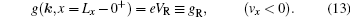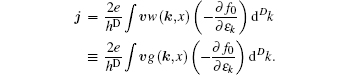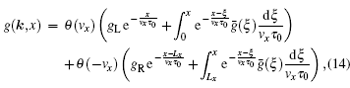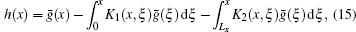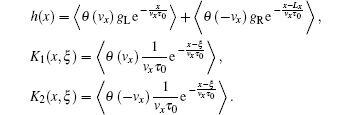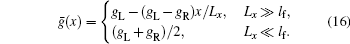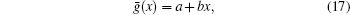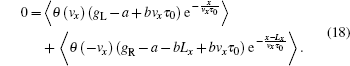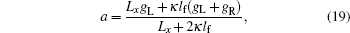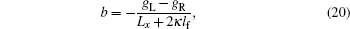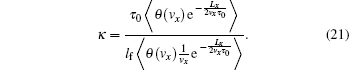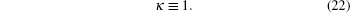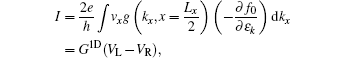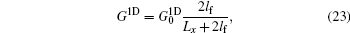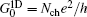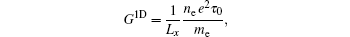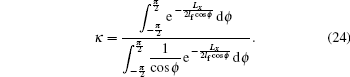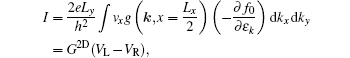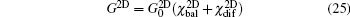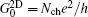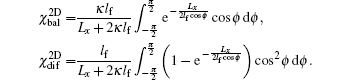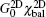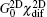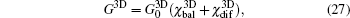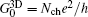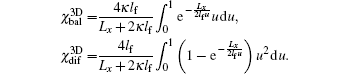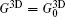Unified semiclassical approach to electronic transport from diffusive to ballistic regimes
1. IntroductionThe Boltzmann equation was first devised by Ludwig Boltzmann in 1872 to describe the state of a dilute gas.[1] In modern literature, the term Boltzmann equation often refers to any kinetic equation that describes the change of a macroscopic quantity in a nonequilibrium thermodynamic system, such as energy, charge, or particle number. The Boltzmann equation has proven fruitful not only for the study of classical gases, but also, properly generalized, for the electron transport in nuclear reactors, the photon transport in superfluids, and the radiative transport in planetary and stellar atmospheres.[2,3] In condensed matter physics, among many successes, an important achievement based upon the Boltzmann equation is the Drude kinetic theory of electrical conduction, which was proposed in 1900 by Paul Drude to explain the transport properties of electrons in macroscopic conductors.[4,5] The Boltzmann–Drude formula for the zero-frequency conductance of a conductor with length Lx and cross section A is
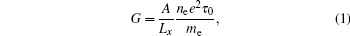
which correctly relates the conductance to the electron density
ne and the relaxation time
τ0 due to the electron scattering by impurities. It works very well for macroscopic conductors, where the sample size is much greater than the electron mean free path (diffusive regime). Moreover, this elegant formula can be reproduced by using modern linear-response theory and Green’s function technique through a deliberate summation of an infinite series of ladder diagrams.
[6]Mesoscopic systems have been subject to tremendous investigations in recent years. Theoretical research on the electronic transport properties of mesoscopic systems is often based upon the transmission approach. In this approach, a conductor is viewed as a target, at which the incident carriers are reflected or transmitted to other probes. The (two-terminal) conductance of a conductor is given by the famous Landauer–Büttiker formula as[7–11]

where
Tn is the transmission coefficient of the
n-th conducting channel, and
Nch is the total number of conducting channels. The Landauer–Büttiker formula was originally proposed based upon phenomenological discussion,
[7–11] and later shown to be equivalent to the Kubo linear-response theory.
[12–14]The size of a mesoscopic conductor can be much smaller than the electron mean free path, and it may even be free of impurities. The Boltzmann–Drude formula fails to behave properly in this ballistic regime. According to the Landauer–Büttiker formula, Tn → 1 in this regime, and the conductance saturates to a finite value G = e2Nch/h. In contrast, the Boltzmann–Drude formula diverges with vanishing impurity scattering (τ0 → ∞). The Landauer–Büttiker formula or its generalization (e.g., (Ref. [15] and [16]) and references therein) has the advantage that it takes the quantum interference effect into full account. This is at the expense that it is usually difficult to apply the quantum theory to macroscopic systems in the diffusive regime. References [17] and [18] were devoted to developing unified theories covering both the ballistic and diffusive regimes. Sophisticated Green’s function calculations were performed, and concrete results were obtained only in some special limiting cases, which make the theories hardly useful in practice. The semiclassical Boltzmann equation approach has the advantage of being simple and intuitive, and often allows us to develop transport theories without laborious calculations, when the quantum interference effect is not important, as is the case in many electronic transport phenomena. Therefore, a reconstruction of the semiclassical approach to make it valid in both the ballistic and diffusive regimes is highly desirable.
In this paper, we show that by integrating out the position-dependent electric field and incorporating proper boundary conditions, a Boltzmann equation can describe electron transport properties of a finite-size conductor, continuously from the diffusive to ballistic regimes. We present both exact numerical and approximate analytical solutions to the Boltzmann equation. General analytical formulas of the conductance in D = 1,2,3 dimensions are obtained, which are consistent with the Boltzmann–Drude formula in the diffusive regime, and recover the Landauer–Büttiker formula in the ballistic regime. This theory can be applied to study the interplay of system size and impurity scattering in various charge and spin transport phenomena.
In the next section, we introduce the Boltzmann equation and associated boundary conditions in our model. Through a linear transformation, the electric field with unknown position dependence is integrated out from the Boltzmann equation. In Section 3, the exact solution of this model is obtained numerically. In Section 4, an analytical approximate theory is developed, and analytical formulas of the conductance in different dimensions are obtained. The final section is the discussion and summary.
2. Model descriptionLet us consider a finite-size conductor of dimension D (D = 1, 2, or 3). The classical nonequibrium distribution function f(k,r) of the electrons in the sample is a function of the phase space point (k,r) with k and r as the momentum and coordinate of an electron. It is assumed that the quantum phase coherence length lφ is smaller than the electron mean free path lf, such that the interference of electron scattering by multiple impurities, as well as the Anderson localization effect, can be ignored. Under this condition, the simple relaxation-time approximation can be employed, and the probability-conserved Boltzmann equation reads [3,19–21]
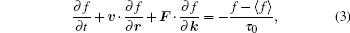
where
F is the external force,
υ =
∂εk/
∂k is the velocity of the electron with
εk =
k2/2
me as the electron energy, the relaxation time
τ0 due to impurity scattering is taken to be independent of
k and
r, ⟨
f⟩ represents the angular momentum average of
f(
k,
r). For example, in three dimensions, by representing the momentum in a polar coordinate system
k = (
k,
θ,
φ), the angular momentum average can be expressed as
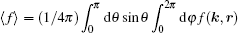
. A unified expression of ⟨···⟩ suitable for all
D = 1,2,3 dimensions will be given later. By integrating over the momentum on both sides of the Boltzmann equation Eq. (
3), one can find that the conservation law of probability is always satisfied.
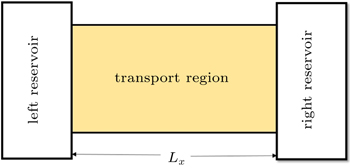
We assume that the conductor is connected to two large reservoirs in regions x < 0 and x > Lx, respectively, as shown in Fig. 1. An electric field E(x) = E(x)êx, with êx as a unit vector along the x direction, is applied across the sample, and so F = eE(x). The electric field is confined in the conductor, and satisfies the constraint 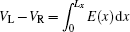 with VL and VR being the electrical voltages at the left and right ends of the sample. The reservoirs remain in equilibrium, and serve as source and drain of the electrical current, so that the electrical current can flow through the sample continuously. The concrete position dependence of E(x) depends on the nonequilibrium charge distribution in the sample. However, we will show that as far as the electrical current is concerned, the result is independent of the profile of E(x).
with VL and VR being the electrical voltages at the left and right ends of the sample. The reservoirs remain in equilibrium, and serve as source and drain of the electrical current, so that the electrical current can flow through the sample continuously. The concrete position dependence of E(x) depends on the nonequilibrium charge distribution in the sample. However, we will show that as far as the electrical current is concerned, the result is independent of the profile of E(x).
To proceed, it is considered that a stationary transport state has been established, so that ∂f/∂t = 0. The electric field is taken to be small, such that we can linearize the Boltzmann equation in the electric field, by writing[20,21]
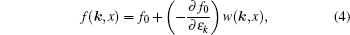
where
f0 = [e
(εk−εF)/kBT + 1]
−1 is the equilibrium Fermi distribution function, and the unknown function
w(
k,
x) is in the linear order of the electric field. By substituting Eq. (
4) into Eq. (
3), we obtain for the Boltzmann equation to the linear order of the electric field
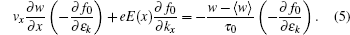
We notice that f0 depends on k only through εk, and so we have ∂f0/∂kx = −vx(−∂f0/∂εk). Using this identity, we can immediately eliminate a common factor −∂f0/∂εk from Eq. (5). As a consequence, the Boltzmann equation reduces to
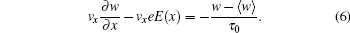
At low temperatures, −∂f0 /∂εk is a delta function. Therefore, for all D = 1, 2, and 3 dimensions, the angular momentum average of ⟨···⟩ can be expressed in a unified form

For right-moving electrons (vx > 0), when they just move across the left interface at x = 0 from the left reservoir into the sample, their distribution function should still be in the equilibrium state, as they have not been accelerated by the electric field. As a result, a boundary condition at the left interface can be written as
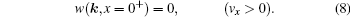
For left-moving electrons (vx < 0), a similar boundary condition exists at the right interface
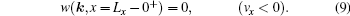
We can eliminate the electric field in the Boltzmann equation, using the following transformation:
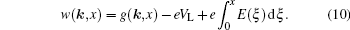
By substitution of Eq. (10), we derive Eqs. (6), (8), and (9) to be
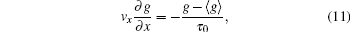
and

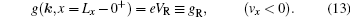
The electric field E(x) with its profile unknown no longer appears in the Boltzmann equation Eq. (11), and instead, electrical voltages VL and VR appear in the boundary conditions Eqs. (12) and (13). It is easy to show that the expression for the electrical current density j is invariant under the above transformation, i.e.,
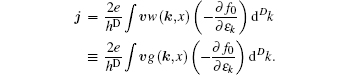
Therefore, g(k,x) plays the same role as w(k,x) does. We point out that the transformation Eq. (10) is valid in the linear regime, and only in this regime, gauge invariance of the physical quantities calculated from Eqs. (11)–(13), with respect to different choices of the electrical voltages VL and VR, is guaranteed. The above derivation proves that the electrical current depends only on the electrical voltage difference across the sample, independent of the profile of the electric field E(x). Owing to this finding, laborious calculations of the electric field from the Maxwell equations are avoided.
We note that ⟨g⟩ is a function of coordinate x only, which will be denoted as ⟨g⟩ ≡ ḡ(x) for clarity in the following formulation. According to the definition Eq. (10), ḡ(x) describes both the effects of the applied electric field and accumulation of carriers ⟨f⟩−f0. From the boundary conditions Eqs. (12) and (13), ḡ(x) has the same unit as the chemical potential. Besides, since the electric field no longer appears in the Boltzmann equation, and it is the gradient of ḡ(x), which drives the electrical current. Therefore, we may call ḡ(x) the effective chemical potential (more strictly, change in chemical potential induced by the applied electric field). Equation (10) may be regarded as a transformation from the representation of charged particles, where the driving force for transport is the electric field, to a representation of neutral particles, where the gradient of the chemical potential causes flow of the particles.
3. The exact solutionA formal solution of g(k,x) can be obtained from the Boltzmann equation Eq. (11) and boundary conditions Eqs. (12) and (13), as a linear functional of ḡ(x) as
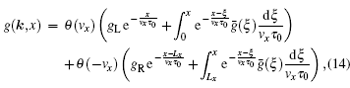
where
θ(
vx) is the unit step function. By taking the angular momentum average on both sides of Eq. (
14), we obtain a self-consistent integral equation for
ḡ(
x),
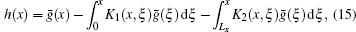
where
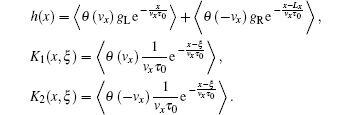
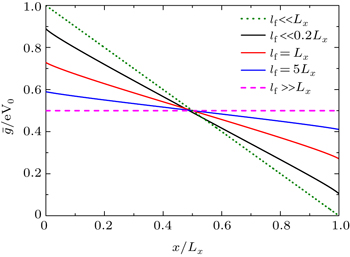
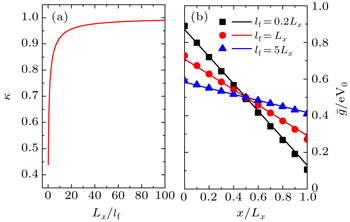
Equations (14) and (15) constitute an exact solution to the Boltzmann equation Eq. (11). One can solve the effective chemical potential field ḡ(x) from Eq. (15), and then substitute it into Eq. (14) to obtain the nonequilibrium distribution function g(k,x). Once g(k,x) is obtained, the nonequilibrium transport properties of the system can be determined. In general, it is not easy to obtain the exact analytical expression for ḡ(x). Before we work out an approximate analytical solution in the next section, we now carry out the numerical calculation. Through discretization of the coordinate x∈ [0,Lx], Equation (15) is reduced to a set of linear equations, which can be solved numerically. The calculated effective chemical potential field ḡ(x) for a two-dimensional sample is plotted in Fig. 2 as a function of x/Lx for several different mean free path to sample length ratios. The mean free path is defined as lf = vFτ0 with vF being the Fermi velocity.
From Fig. 2, we see that ḡ(x) is exactly a linear function of x in two limits Lx ≪ lf and Lx ≫ lf. In fact, it is easy to obtain from Eq. (15) that
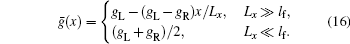
When Lx is comparable to lf, a linear dependence is still valid in the middle region of the sample, but tiny deviations from the linear dependence occur near the sample boundaries x = 0 and x = Lx. In Fig. 2, sudden jumps of the effective chemical potential ḡ(x) occur at the boundaries, x = 0 and x = Lx. These jumps can be understood as due to the contact resistances between the sample and reservoirs.[25] In the ballistic limit, the sample is ideal and the contact resistances dominate. The effective chemical potential can only jump at the boundaries, as illustrated by the pink dashed line in Fig. 2. In the opposite diffusive limit, the bulk resistance of the sample overwhelms the contact resistances, and the jumps of ḡ(x) at the boundaries are less obvious, as can be seen from the green dotted line. This behavior is very like the similar phenomenon in the ballistic-to-diffusive heat transport in silicon nanofilms and carbon nanotubes,[26–29] observed in Monte Carlo simulations and Molecular dynamics simulations.
4. An analytical approximationAs has been observed in Section 3, the exact solution of the effective chemical potential ḡ(x) is nearly a linear function of coordinate x with negligible deviations occurring near the sample boundaries in the region Lx∼ lf. Therefore, it is reasonable to make a linear approximation to ḡ(x), assuming
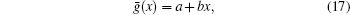
with
a and
b as two constant coefficients to be determined. Substituting this trial solution into Eq. (
15), we can obtain the following equation for
a and
b:
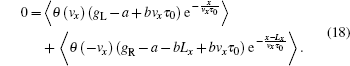
To determine the coefficients a and b, one can choose two different values of coordinate x in the above equation to obtain a couple of equations of a and b. Noticing that the linear dependence of ḡ(x) on x is very well satisfied in the middle region of the sample, we choose x = Lx/2 and x = Lx/2 + Δx, and take the limit Δx → 0 in the final solution. We obtain
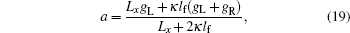
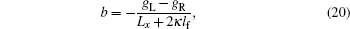
where
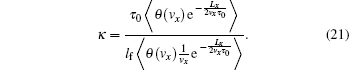
Notebaly, equation (17) together with Eqs. (19) and (20) recover Eq. (16) in two limits Lx ≫ lf and Lx ≪ lf.
4.1. One dimensionFor D = 1 dimension, in Eq. (21), vx ≡ vF, and so
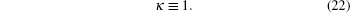
Interestingly, we notice that if we substitute Eqs. (19) and (20) with κ = 1 into Eq. (18), both terms on the right-hand side of Eq. (18) vanish identically for any x. This means that for D = 1, equation (17) is actually an exact solution to Eq. (15). Therefore, the conductance formula obtained below for one-dimensional systems is an exact result of the Boltzmann equation. Since the electrical current I is constant along the x direction, we calculate I setting x = Lx/2, yielding
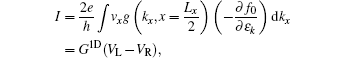
where
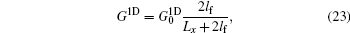
is the conductance of the system. Here,
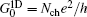
, with
Nch = 2 taking into account the spin degeneracy. We note that the electrical current
I depends only on the voltage difference (
VL −
VR) between the two ends of the sample, which is a manifestation of the gauge invariance. In the ballistic limit
Lx ≪
lf,

, being consistent with the Landauer–Büttiker formula. In the diffusive limit
Lx ≫
lf
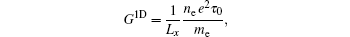
with
ne = 4
kF/
h as the electron density, which recovers the well-known Boltzmann–Drude formula.
4.2. Two dimensionsIn D = 2 dimensions, by using a polar coordinate system, we obtain
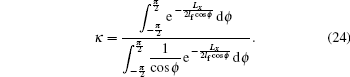
The calculated κ is plotted in Fig. 3(a) as a function of Lx/lf. With increasing Lx/lf from 0, κ increases from 0 and then approaches 1 rapidly. In Fig. 3(b), the approximate solution ḡ(x) = a + bx, with a and b given by Eqs. (19) and (20), is plotted as solid lines for some different values of Lx/lf. The exact solution of ḡ(x) is also shown as symbols in Fig. 3(b). The approximate solution fits very well with the exact solution. The electrical current at x = Lx/2 is calculated, yielding
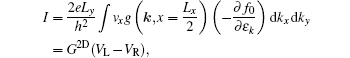
where
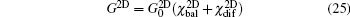
is the conductance of the two-dimensional sample. Here,
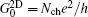
, where
Nch = 4
kFLy/
h is the channel number with
Ly as the cross-section length of the sample, and
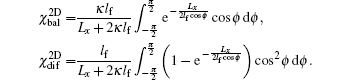
The total conductance is divided into two parts: 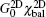 and
and 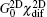 , standing for contributions from electron ballistic and diffusive transport processes, respectively. In the ballistic limit Lx ≪ lf, χbal → 1 and χdif → 0, such that
, standing for contributions from electron ballistic and diffusive transport processes, respectively. In the ballistic limit Lx ≪ lf, χbal → 1 and χdif → 0, such that  , being consistent with the Landauer-Büttiker formula. In the diffusive limit Lx ≫ lf, χbal → 0 and χdif → πlf/(2Lx), and so G2D = (Ly/Lx)(nee2τ0/me), with
, being consistent with the Landauer-Büttiker formula. In the diffusive limit Lx ≫ lf, χbal → 0 and χdif → πlf/(2Lx), and so G2D = (Ly/Lx)(nee2τ0/me), with  as the electron density, recovers the Boltzmann–Drude formula.
as the electron density, recovers the Boltzmann–Drude formula.
4.3. Three dimensionsIn D = 3 dimensions, we obtain

The conductance is derived to be
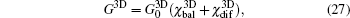
where
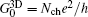
with

with
A as the cross section and
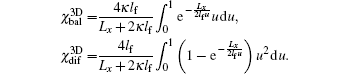
In the ballistic limit Lx ≪ lf, χbal → 1 and χdif → 0, and hence 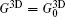 , in agreement with the Landauer-Büttiker formula. In the diffusive limit Lx ≫ lf, χbal → 0 and χdif → 4 lf/(3Lx). As a result, G3D = (A/Lx)(nee2τ0/me), with
, in agreement with the Landauer-Büttiker formula. In the diffusive limit Lx ≫ lf, χbal → 0 and χdif → 4 lf/(3Lx). As a result, G3D = (A/Lx)(nee2τ0/me), with  as the electron density, reproduces the Boltzmann–Drude formula.
as the electron density, reproduces the Boltzmann–Drude formula.
We wish to point out that for both D = 2 and 3, a further simplification of the theory can be done by setting κ = 1. From Fig. 3(b), we see that κ has large deviations from 1 for Lx ≲ lf. Fortunately, as can be seen from Eqs. (25) and (27), the conductance becomes insensitive to the value of κ in the region Lx ≲ lf. In Fig. 4, the conductance for D = 2 calculated by using κ = 1 is compared with that obtained by using the expression Eq. (24) for κ. The difference between them is nearly invisible, an indication that setting κ = 1 is a very good approximation for most purposes.
5. Discussion and summaryIn summary, we have demonstrated that the Boltzmann equation together with proper boundary conditions can describe electron transport properties from diffusive to ballistic regimes. We have worked out a sufficiently accurate analytical solution to the Boltzmann equation. Analytical formulas of the electrical conductance for D = 1, 2, and 3 dimensions are obtained, which smoothly bridge the Boltzmann–Drude formula in the diffusive regime and Landauer Büttiker formula in the ballistic regime. This simple and intuitive approach can be applied to investigate the effects of sample size and impurity scattering in various charge transport phenomena. For example, temperature difference can also drive electric current, which is also characterized by the Boltzmann equation.[30] In the present approach, one can consider that the two reservoirs are in local equilibrium states with different temperatures, which will modify the boundary conditions Eqs. (12) and (13) for the electron distribution function. Then the thermoelectric transport properties of the system can be studied in the same manner.
Spin-dependent electronic transport has attracted a great deal of interest in recent years.[22] To describe spin-dependent transport, some essential generalizations of the present theory need to be done. First, a spin relaxation mechanism needs to be included.[23] Second, the effective chemical potential field ḡ(r) defined in the present theory includes the effects of the applied electric field and accumulation of particles. In a spin-dependent transport process, while the physical electric field is always spin-independent, the accumulation of particles can become spin-dependent, resulting in the so-called spin accumulation. Therefore, a spin-dependent effective chemical potential field ḡs(r) can be assumed to account for the effects of spin accumulation and spin diffusion.[23,24]