† Corresponding author. E-mail:
In this article, we review recently achieved Kerr effect progress in novel liquid crystal (LC) material: vertically aligned deformed helix ferroelectric liquid crystal (VADHFLC). With an increasing applied electric field, the induced inplane birefringence of LCs shows quadratic nonlinearity. The theoretical calculations and experimental details are illustrated. With an enhanced Kerr constant to 130 nm/V2, this VADHFLC cell can achieve a 2π modulation by a small efficient electric field with a fast response around 100 μs and thus can be employed in both display and photonics devices.
Recently, liquid crystal phase modulators with constant ellipticity enjoy great popularity because of their fast response and low-power-consumption characteristics for various applications for displays and photonics. These devices include tunable gratings, beam steering, focal lenses, wave-front correctors, etc.[1–4] Nematic liquid crystals are the most common ones used for photonic components. However, nematic LCs have their essential problems functioned as a phase modulator. Phase modulators usually call for a 2π modulation to be widely used in the photonic devices mentioned above. Thus, it is necessary to increase the thickness of the nematic LC cell to meet the 2π modulation requirement. This will sacrifice the NLC response, and several efforts are therefore devoted to exploring the possibilities of other LC electro-optical modes for the high-speed phase modulations.
In order to achieve the response time, some faster switching LC modes have been proposed such as the polymer-stabilized blue phase (PSBPLC) and chiral nanostructured devices based on the Kerr effect.[2,4–9]
The Kerr effect for the PSBPLC is explored in some works in recent years. BPLC is famous for its sub-millisecond response and having no need for an alignment layer due to its self-assembled cubic structure. However, it is also characterized by a relatively small phase change and a disclination line induced limited operation temperature range. Although the new class of PSBPLC recently reported in Ref. [10] discloses a higher value of the Kerr constant, several issues still exist. Firstly, the fabrication process is quite complicated as ultraviolet curing at a precise temperature within the LC blue phase or isotropic phase is needed. Secondly, the mixture consists of several different kinds of components,[8–10] making the material preparation difficult. Thirdly, the electrical–optical hysteresis and high driving voltage are not suitable for real devices.
Ferroelectric liquid crystals (FLCs),[11–16] as another kind of ultra-fast response liquid crystals, are a promising candidate for modern applications. However, most of the FLC modes, like the earliest surface suppress helix mode, deformed helix modes[17] and electrically suppressed helix ferroelectric liquid crystal which also has many applications[18,19] in display areas, are not good candidates for pure phase modulation. As their optical axis switches in the plane parallel to the cell substrate, the polarization state of the outgoing light will remain the same as the incident light. In order to get rid of the optical axis switching issue, we investigated the phase modulation in vertically aligned deformed helix ferroelectric liquid crystal (VADHFLC) cells,[20,21] where the optical axis of the FLC cell is perpendicular to the substrates and the helix pitch of the FLC material, p0, is short compared to the wavelength of light, λ. Electro-optical properties of the VADHFLC cells with this subwavelength helix pitch are studied both theoretically and experimentally. The theoretical equation deduction for the induced refractive index difference and the Kerr constant of homeotropic VADHFLCs with the subwavelength pitch are discussed in Section 2.1. Section 2.2 mainly talks about the experimental procedures and measurement setups. It turns out that the experimental Kerr constant of the VADHFLC mode used to achieve the 2π phase modulation is in agreement with the results of the theoretical calculation. Thus, it has been proven that optical anisotropy of subwavelength pitch VADHFLCs is found to be generally biaxial, and in the low-voltage regime, the electric field dependence of the birefringence exhibits the quadratic nonlinearity that can be called the orientational Kerr effect.
The VADHFLC exhibits zero-field uniaxial optical birefringence while the optical axis is parallel to its twisting helix. With a sufficient weak electric field generated by interdigital electrodes, the FLC shows the optical biaxial and induced inplane birefringence is quadratically proportional to the electric field magnitude, and this phenomenon is interpreted as orientational Kerr effect.
Ferroelectric liquid crystals, developed in 1975, are famous for their surface suppressed helix. Nowadays, they become more popular due to the discoveries of new operational modes utilized in display applications: deformed helix ferroelectric liquid crystal (DHFLC) and electrically suppressed helix ferroelectric liquid crystal (ESHFLC).[21–23] Recently the Kerr effect in a new mode is found by Pozhidaevetc.[20,24] With vertically aligned deformed helix geometry of the FLC cell, the incident light can have a 2π phase modulation of 534-nm with the in-plane rotations of the optical axis suppressed.
Figure
 | Fig. 1. (a) The geometry of the VADHFLC mode with electric field applied by interdigital electrodes. (b) The working principle of electric field induced in-plane birefringence of the average refractive index ellipsoid.[20] |
The optical properties of the subwavelength pitch (P ≪ λ) VADHFLC are illustrated in Fig.
For normally incident light, the refractive index perpendicular (parallel) to the electric field reads


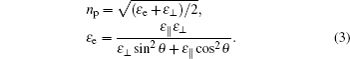

From the equations above, the electrically induced in-plane birefringence can be expressed as
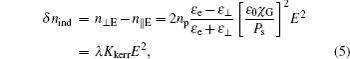

The calculation results are further proved by experiments. In the experiments, the testing material: FLC-587, an eutectic mixture of three compounds (chemical structures are shown in Fig.
 | Fig. 2. Chemical structures of the components in FLC mixture-587.[20] |
The FLC material parameters are as follows: Ps = 160 nC/cm2, θ = 35°, and the helix pitch p0 = 0.18 μm at 22 °C. The FLC phase transition sequence is
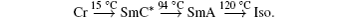

 | Fig. 3. The transmittance and induced birefringence versus the square of applied electric field of VADHFLC cell placed between two crossed polarizers. The insert figure is the Kerr constant dispersion.[20] |
According to the experimental data (the square), the δnind(E2) shows a linear increase and saturates at about 0.05, which is roughly in accordance with the theoretic curve (red solid line) calculated with the parameters of DHFLC measured at 60 °C: ε⊥ = 2.3; ε∥ = 3.1; χ = 50.
The inserted figure shows that in the frequency region f < 2 kH, Kkerr maintains a constant: Kkerr = 27 nm/V2, which is roughly two orders of magnitude greater than the Kerr constant of nitrobenzene and twice as large than the highest Kerr constant of PSBPLC. In the high-frequency region f > 2 kHz, Kkerr decreases and shows a pronounced dispersion.
As for the geometry mentioned in Fig.
 | Fig. 4. The open circles represent the ellipticity of the 534-nm transmitted light measured at φ = 90°, while the solid circles represent the induced birefringence of 10-μm-thick cell.[20] |
It should also be noticed that the Kerr constant is dependent on the temperature. In Fig.
 | Fig. 5. Temperature dependence of Kerr constant of VADHFLC from 20 °C to 60 °C measured with 534-nm incident light.[20] |
Although we achieve a more pronounced Kerr effect than the modern popular PSBPLC, it is necessary to increase the Kerr constant of the VADHFLC further to meet the high demand of low voltage modulation of light.
From the Kerr constant equation, it is very clear that the increase in the spontaneous polarization Ps and the pitch p0 will cause enhancement of the Kerr constant. However there are some constraints on these parameters: firstly, to avoid the selective reflection in the visible range, the pitch of the FLC should be small enough; secondly, an increase in Ps should be realized by adding more chiral molecules which will also increase the rotational viscosity γΦ. Such an increase will slow down the electro-optical response of the VADHFLC. Hence, there is a trade-off between a high Kerr constant and a fast EO response. Only by carefully choosing the chemical structures of the FLC mixture components can we optimize the relationship between the parameters γΦ, Ps, p0, K, and θ to get an increased Kerr constant within the defined limitations.
An FLC mixture-618 is designed to meet these constrains. The mixture consists of two chiral nonmeogenic compounds (Figs.
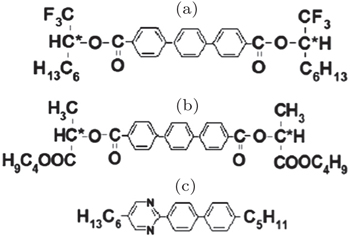 | Fig. 6. Chemical structures of the components in FLC mixture-618.[24] |
With the weight concentration of components corresponding to a certain ratio, the FLC-618 is synthesized and its parameters characterized at 60 °C are shown for comparison with FLC-587.
The Kerr constants shown Table 

| Table 1. Kerr constant.[24] . |
In conclusion, the orientational Kerr effect in VADHFLC with a large Kkerr constant (27 nm/V2 at 534 nm) has been proved by both theoretical analysis and experimental data. The 2π modulation of light with a fast response of 100 μs, constant ellipticity of transmitted light and hysteresis free electro-optics give rise to opportunities in both display and photonics applications. The low power consumption of these devices can be further achieved by increasing the Kkerr constant to 130 nm/V2 at 534 nm through optimizing the parameters of FLC materials under certain constraints like UV selective reflection and fast EO response.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 |


