† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 41474161) and the National High-Technology Program of China (Grant No. 2015AA123703).
In order to satisfy the requirement of SI-traceable on-orbit absolute radiation calibration transfer with high accuracy for satellite remote sensors, a transfer chain consisting of a fiber coupling monochromator (FBM) and an integrating sphere transfer radiometer (ISTR) was designed in this paper. Depending on the Sun, this chain based on detectors provides precise spectral radiometric calibration and measurement to spectrometers in the reflective solar band (RSB) covering 300–2500 nm with a spectral bandwidth of 0.5–6 nm. It shortens the traditional chain based on lamp source and reduces the calibration uncertainty from 5% to 0.5% by using the cryogenic radiometer in space as a radiometric benchmark and trap detectors as secondary standard. This paper also gives a detailed uncertainty budget with reasonable distribution of each impact factor, including the weak spectral signal measurement with uncertainty of 0.28%. According to the peculiar design and comprehensive uncertainty analysis, it illustrates that the spectral radiance measurement uncertainty of the ISTR system can reach to 0.48%. The result satisfies the requirements of SI-traceable on-orbit calibration and has wider significance for expanding the application of the remote sensing data with high-quality.
In recent years, global warming and earth observation with high resolution and extreme disaster forecast have become a hot topic, therefore the demand of high-quality remote sensing data traced to unified radiation standard is becoming more and more urgent.[1] The radiometric calibration accuracy directly determines the use value of the remote sensing data. So far, two methods have been proposed for on-orbit spectral radiometric calibration. One introduced the solar radiation into remote sensors for calibration through a diffused reflection device.[2,3] For example, the RSBs of MODIS (moderate-resolution imaging spectroradiometer) instrument on the Aqua satellite were calibrated by SD/SDSM (solar diffuser and solar diffuser stability monitor) system.[4] The other set standard radiation sources (halogen tungsten lamp, blackbody source, etc.) on the payload for sensor calibration,[5] such as the SOLSPEC (SOLarSPECtrum) instrument in the SOLAR payload.[6] Due to many factors affecting the attenuation of the sensor-response in the space, the uncertainty and stability of above calibration methods are not satisfactory. However, there is no united SI-traceable radiometric benchmark for on-orbit radiation calibration currently, thus the deviation of spectral radiance calibration between different platforms can sometimes be as large as 10%,[7] which eventually results in a great waste for data resources. Therefore, establishing an on-orbit calibration transfer chain for SI-traceable benchmark with high-accuracy has become a future research direction of on-orbit radiometric calibration.
The uncertainty level of the current on-orbit radiometric calibration method is about 10−2 scale.[8] MODIS, whose on-orbit performance is about 2%–4%,[4] is generally accepted as the on-orbit reference standard. In contrast, the uncertainty of SOLSPEC on-orbit calibration is about 4%.[6] However, to meet the demands of meteorological research, the on-orbit calibration accuracy needs to be 10−3 scale,[9] which has a large gap with the current calibration method. To solve the problem above, a new radiometric calibration transfer technology based on a cryogenic radiometer was proposed and the feasibility of this transfer chain was demonstrated in this paper.
CIOMP (Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences) is working on developing a calibration transfer system that uses a cryogenic radiometer as the space-based spectral radiation benchmark and uses the Sun as the calibration source. This system is composed of an FBM (fiber coupling monochromator) and an ISTR (integrating sphere transfer radiometer). FBM is used to accomplish absolute calibration of monochromatic light power and ISTR is used to measure the spectral characteristics of SDP (solar diffuser plate). This transfer system (ISTR system) ultimately achieves the absolute spectral radiation calibration transfer from on-orbit radiance reference standard to optical payloads with a breakthrough in the uncertainty of 0.5%. The ISTR system aims to establish a formula of controlling data quality and data accuracy to standardize satellite sensors calibration. This formula can ensure that all of the directly acquired data and active data products are able to trace to SI truly and effectively. Then it can eventually achieve the systematization, normalization, and standardization of radiometric calibration with high accuracy for remote sensors.
The purpose of this paper is to provide an overview of the operating principle for the SI-traceable ISTR system and an uncertainty budget to evaluate its calibration performance. An overview of the transfer chain design will be presented in Section 2. Section 3 will provide a comprehensive and reasonable uncertainty analysis for the whole system. The summary and prospects are set out in Section 4.
In the purposes of establishing the SI-traceable on-orbit calibration transfer chain based on spectral radiation standard for satellite remote sensors, CIOMP consults some mature technology for transfer radiometers used in other metrology research institutions, such as SXR (sea WiFS transfer radiometer)[10,11] designed by NASA, and PTR (polarize transfer radiometer) designed by ESA.[12] CIOMP developed an ISTR system with an innovative transfer technology that is suitable for the absolute radiometric calibration taking the Sun as an invariable source.[13] The ISTR system takes ISTR as the core equipment and it integrates the functions of integral sphere light source and spectral standard calibration transfer. It also achieves the conversion from cryogenic radiometer benchmark to radiance standard with the assistance of FBM, and it realizes the goal of calibrating and measuring other on-orbit remote sensors. The components of the system are shown in Fig.
 | Fig. 1. Schematic diagram of the SI-traceable calibration and traceability chain of the ISTR system. |
ISTR is composed of three components, an integral sphere shell with a dual-aperture field stop, a filter radiometer (FR), and a photoelectric measurement module (PMM). Therefore, it can work as a secondary standard[14] or a filter spectral radiance working standard. ISTR can achieve the traceability from trap detectors to the SI-traceable cryogenic radiometer benchmark through using FBM output narrow-band monochromatic light whose power is calibrated by the cryogenic on-orbit radiometer.[15] ISTR can also complete the inner calibration for filter radiometer. Coupling with the dual-aperture field stop, it can implement the conversion between power and radiance. Through this conversion, ISTR can accomplish the calibration standard transferring from the above reference standard to payloads such as imaging spectrometers. The whole process is shown in Fig.
The function of the FBM in the ISTR system is outputting monochromatic light whose power is calibrated by a cryogenic radiometer through moving the bended fiber on the rail. It can transfer the power benchmark to ISTR to achieve the radiance standard calibration by FBM. The transfer accuracy is mainly limited by the low power level of the monochromatic light when using sunlight as the spectral on-orbit radiometric calibration source. Currently, most monochromators adopt the light dispersing methods of grating or interferometry, which can obtain high-quality monochromatic light with an accurate central wavelength and an extremely narrow bandwidth.[6] However, in consideration of the limitation of the minimum detectable power of the cryogenic radiometer and the measurement accuracy of 0.5%, the output power of FBM should be larger than 1 μW. Meanwhile, the output power scales between FBM and SDP should be as similar as possible for improving the measurement accuracy of the radiance reflected by SDP. Therefore, FBM uses the double-grating type, which is suitable for an on-orbit ISTR system, to get monochromatic light with an accurate central wavelength and a narrow bandwidth but lower power. To increase the output power, it adopts gratings with high efficiency, parabolic mirrors with high reflectance, and fibers with high coupling efficiency.
FBM is composed of three parts, a pre-convergent parabolic mirror used to collect the incident solar light, the double-grating monochromator for light dispersing, and a fiber system to export the monochromatic light. The monochromator adopts four off-axis parabolic mirrors and two gratings, the optical configuration is central symmetry about the central slit, as shown in Fig.
Considering the solar light is not ideally collimated (with a divergence angle of 0.5°), the pre-convergent mirror is designed to image at the entrance of the monochromator and fill the slit, then we can obtain



The spectral irradiance of the Sun distributes irregularly in the range of 0.3–2.5 μm, E(λ)Sun at 15 typical central wavelengths of the monochromator as shown in Table
| Table 1. Parameters of typical channels. . |
ISTR receives the monochromatic light output from FBM and then the power primary standard traced to cryogenic radiometer is converted to radiance working standard by using a dual-aperture field stop. Relying on the Lambertian property of the integral sphere, the uniform output radiance of ISTR is


Combining the above analysis of the parameters with the actual limitation of the payload in space, the final design of ISTR adopts the sphere diameter of 80 mm with the input port diameter of 10 mm. A field stop composed of two precision apertures is used as a power-to-radiance standard converter in front of the input port when the light fills the field stop. The two apertures are 20 mm apart with diameters of 16 mm and 10 mm respectively. The equation of the standard conversion process is


ISTR has two exit ports with the same diameters of 6 mm, which are connected with an FR and a PMM, respectively. For improving the spatial uniformity of the output radiance, a baffle is mounted between the incident plane and the exit ports. The baffle can prevent the first reflected light outputting from ISTR directly and increase the reflection number of the incident light in ISTR. The inner surface of ISTR is coated with Spectralon@ material and its reflectance is greater than 0.99 in the range of 400–1500 nm and greater than 0.95 in the range of 250–2500 nm. The schematic of the ISTR configuration is shown in Fig.
PMM is mounted in front of one of the integral sphere exit ports, it is composed of Silicon and InGaAs trap detectors and a signal control circuit.[18] Going through the integrating sphere, the FBM output spectral power turns to a uniform weak radiance signal. Then, the trap detector receives it and works as a secondary standard traced to the cryogenic radiometer primary power standard to calibrate the FR. The incident spectral power exported from the integral sphere into the trap detector is ϕdet(λ)


The weak radiation signal is easy to be submerged in the noise if received by PMM directly, especially in the near infrared spectrum of 1200–2500 nm. Because the primary mission of on-orbit ISTR is to measure the radiance reflected by SDP with high precision, it needs to keep the power used to calibrate the detector similar to the power measured by the detector. The spectral power entering ISTR directly from SDP will be only 10−10 W scale due to the lack of concentrating light like FBM, thus, we cannot simply enhance the output power of FBM to solve the signal measuring problem above.[19] A light modulating system (for both PMM and FR) should be introduced to make the spectral radiance measurement accuracy 0.3%.
The light modulator locates in front of PPM and carries out high-accuracy electronic measurement with digital phase-sensitive detection technique, the whole control principle is shown in Fig.
The input signal is shaped to be a rectangular wave through the SR830 with a high fidelity sine wave as the reference signal. Then, the synthetic source does phase lock based on the reference signal, which is

This measuring method modulates the input optical signal with the chopper’s frequency and make it able to be expressed in the following rectangular wave:



In practice, the value of phase θ is constant, the measuring accuracy of 


For the light modulator system above, the light chopper selects a three-hole cutting disc and the frequency is set to be 100 Hz with peak-to-peak phase accuracy of 0.1%. It means that there is a 0.2π-phase error generated per second. Depending on the 0.2-s amplifier time, the relative uncertainty δU calculated from Eq. (
The filter radiometer will be utilized to measure the spectral radiance emitted from SDP in space and is the main task of the ISTR system operating on-orbit. Through measuring a series of spectral power at different central wavelengths with a narrow bandwidth by FR, the curve of the relative spectral response function (SRF) can be calculated by a smooth interpolation fitting method.[20] According to the predictability of relative spectral responsivity, the calibration for the whole solar reflective spectrum could be accomplished. FR is connected with the other exit port of the integral sphere and receives the uniform output radiance. FR finally selects 15 spectral channels with interference filters of OptoSigma-VPF series, covering 300–1000 nm, 1000–1600 nm, and 1600–2500 nm with corresponding spectral resolution of 3 nm, 5 nm, and 10 nm in sequence. FR uses the same Silicon trap detector with PMM for the 11 spectral channels covering 300–1100 nm spectrum under 300 K working temperature, and the same InGaAs trap detector for the channels over 1100–2500 nm under cryogenic environment of 240 K controlled by the mechanical refrigerator. The distribution of these 15 channels is determined upon the smoothness and complexity of the SRF curve of the Sun (shown in Fig.

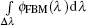





As the stability of the detectors in the cryogenic environment is extremely high and the precision of the uniformity of the integral sphere output radiance can be 0.1%, the accuracy of the radiometric standard transfer can reach to the level of 0.3% in the traceability calibration process above. The FR will measure the spectral radiance emitted from the SDP through the digital phase sensitive detection technology described in Section 2.4. The main parameters and technical indicators of the whole system are summarized in Table
| Table 2. Specifications of ISTR system. . |
The whole process of the radiometric standard calibration transfer through the ISTR system is as follows. Firstly, the cryogenic radiometer was utilized to calibrate the output spectral power of FBM, and then the well-calibrated FBM was applied to calibrate the spectral power responsivity of the PMM, which is used as the secondary standard to calibrate the spectral power responsivity of the FR. Subsequently, achieving the conversion from power standard to radiance standard through the dual-aperture field stop, and finally completing transferring the radiance standard to other satellite remote payloads through the measurement of the spectral radiance emitted from SDP, it can realize the SI-traceable on-orbit radiometric standard calibration transfer with the whole united uncertainty of 0.5% and accomplish the mission of making ISTR as the on-orbit radiance reference standard for all the satellite optical payloads. In order to evaluate the measurement uncertainty, an accurate measurement equation to express the whole process using the ISTR system above, refer to Eqs. (
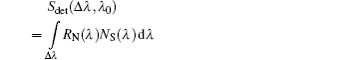


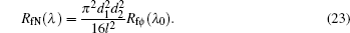
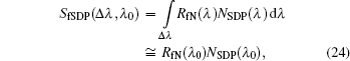
| Table 3. Uncertainty component contribution to the radiance calibration and measurement of the whole ISTR system. . |
Combining parameters used in Eqs. (
This paper introduces the space-based spectral radiation standard calibration transfer system which consists of FBM and ISTR instruments. The ISTR system covers the spectral range of 300–2500 nm with a channel bandwidth of 3–10 nm, it can achieve 105 dynamic range of the spectral radiance measurement with the accuracy of 0.48%.
Aiming to work as the new generation of on-orbit radiance reference standard, the ISTR system innovatively adopts the combination of a cryogenic radiometer, an FBM, an integral sphere radiometer, and an FR radiometer. The ISTR system eventually achieves the SI-traceable on-orbit calibration of the spectral radiance based on the solar radiance through the appropriate design after careful consideration with advanced precise calibration technology. Compared with other traditional transfer radiometers, the ISTR system has the characteristics of high-level integration, light load, large dynamic range, wide spectrum coverage, and short calibration transfer chain with low-level uncertainty. Relying on the outstanding capacity of detecting an extremely weak light signal with high accuracy, the ISTR system is specially designed for the on-orbit radiometric calibration system, which serves Chinese future satellite payloads to trace back to SI based on a cryogenic radiometer as the primary power standard. It is the prerequisite for achieving a breakthrough to the accuracy of the absolute radiometric calibration for Chinese remote sensors, which can be depressed to the 1% scale. The ISTR system is also a project aiming at establishing an on-orbit metrology laboratory, which is similar to NASA’s CLARREO[21] and ESA’s TRUTHS,[9] to provide SI-traceable absolute radiometric calibration services for all the satellites. There is still no such calibration transfer system currently. Along with the future research on the combination of SDP and on-orbit cryogenic radiometer, the ISTR system will build the SI-traceable on-orbit calibration chain for remote sensors in the visible and near infrared spectrum with high measurement accuracy.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 |







