Chaos is a kind of nonlinear phenomenon. A chaotic system is sensitive to the initial conditions and shows some random behaviors, different starting conditions result in many different kinds of dynamic orbits. It is very difficult to predict the chaotic long-term behavior.^[1–3] However, characteristics and laws behind chaos are gradually discovered.^[4–8] In the 1990s, the “OGY” chaos-control method was presented,^[1] the study of chaos-control has been rapidly developed;^[6–11] the parameter chaos control, the adaptive chaos control, the fuzzy chaos control, and so on have been presented.

Nonlinear devices, e.g., semiconductor lasers, are easily subjected to external feedback and can be destabilized to chaotic oscillation.^[3–8] For applications requiring stable operation, the chaos control is very important. On the other hand, in the last two decades, some applications of chaos have been proposed and developed, such as optical chaos communication, chaotic radar, chaotic OTDR, and physical random number generation.^[12–15] Therefore, the generation of chaos laser, i.e., chaos-anti-control of laser, becomes equally important. We can use some techniques to suppress chaos laser or guide laser into some states.^[6–11] Many chaos-control methods are proposed to suppress or stabilize chaotic laser. There are the current perturbation method, the delay feedback method, the injection period signal method, the phase modulation method, the double split feedback method, the injection chaotic signal method, and so on.^{[6–11,16–18]}

A twisted fiber has the birefringence property. The polarization light passed through the twisted fiber results in a delayed phase, an optical rotation, or an optical axis deflection. Using the characteristic of the twisted fiber, we present a novel semiconductor laser system with a twisted fiber as the optical delayed feedback path. It is a novel idea to introduce some physics effects to guide the laser behavior or chaos-anti-control of the laser. It will be a new research area of chaos-control or laser techniques by using physics characteristics and especial effects. We focus on the chaos-anti-control and dynamics in the laser by introducing the physics effects of the twisted fiber. The laser system is very helpful to study other laser systems and chaos-control.^[19]

The delay negative feedback semiconductor laser with an external cavity is a nonlinear optical system, which has been widely studied in theory and experiment. As a result of the optical re-injection of the delayed feedback, the laser has some stable or unstable nonlinear phenomena, such as a period, a multi-period and bifurcation or chaos.^[6–10] In order to structure a new laser system with delayed dual-feedback characteristic and study the control or anti-control laser, we design first a controllable ring path using a twisted fiber to structure a new combination of the delayed feedback and ring laser system. Figure 1 shows a schematic block of the laser using a twisted fiber. In order to simplify the theory model, the laser may be considered as single-polarization lasing.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic block of the laser using a twisted fiber. M1 is the semireflecting mirror, M2 is the plane mirror, BS is a beam splitter, and PC1 and PC2 are two polarization controllers.

Here, the optical path of the laser system is designed as follows. A beam of light after PC₁ is divided into two beams by the beam splitter BS, a bunch of light is reflected by the semireflecting mirror M₁ back to the laser, the optical path of the laser and the mirror M₁ constitute the known external cavity delayed feedback laser. Under certain conditions, the laser can show cycle or chaos operation. Another bunch of light passes through the twisted fiber, and then through the polarization controller PC₂ and re-injects to the laser via the mirror M₂, where PC₂ controls the polarization direction and the re-injection level of the light because the polarization rotation of light occurs when the light passes through the twisted fiber. The combining of the fiber and PC₂ is used as a control.

The twisted fiber is spinning at rate ξ and the fiber has birefringence Δβ, the light passes through the fiber; at length z, the phase delayed R(z), the rotation angle Ω(z), and the optical axis deflection angle Φ(z) can be obtained as^[20]

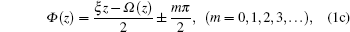
Next, we focus on the following two cases in this work. 1)

For a low twisted rate ξ ≪ Δβ, we obtain Φ(z) ≈ 0, namely, the optical axis cannot vary. The delayed phase and the rotation angle are obtained as

We consider the twisted fiber effects on the laser system, the dynamic equations of the laser with the twisted fiber are obtained as follows:^[5–12]

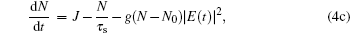
In our numerical simulations, the laser parameters are cited from Ref. [7] and other parameters are taken as r₀ = 0.556, r₁ = 0.006, and τ₁ = 1 ns. We use the parameters of the twisted fiber in the practical value range, in which we take ξ ≤ 600 rad/m considering that the twisted fiber will be twisted broken when the spinning rate ξ is higher than 2π × 10³ rad/m and Δβ ≤ 160 rad/m because the modern optical fiber technology can produce Δβ higher than 200 rad/m. The parameters of the twisted fiber are taken as Δβ = 60 rad/m, G = 0.08, ξ = 6 rad/m. The refractive index is taken as 5/3 and the transmission time τ₂ stands for the twisted fiber length as a control parameter to shift the two parameters of the delayed phase and the rotation angle. The factor r₂ related to the feedback level and the factor τ₂ related to the twisted fiber length as the control parameters are adjusted. Figure 2 shows a periodic state of the laser when the twisted fiber is not present, the laser oscillates periodically at 1.95 GHz after 20 ns.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The laser emits a periodic pulse after 20 ns.

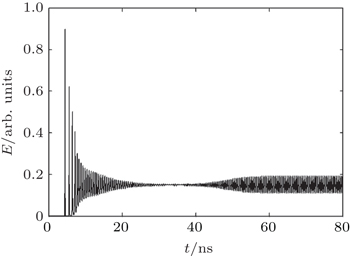
When the control operation is carried out and the control parameters are taken as r₂ = 0.008 and τ₂ = 2 ns, the laser is conduced to show a beat after 20 ns while the beat frequency is about 0.22 GHz. A comparison of Figs. 2 and 3 illustrates obviously the effect of the twisted fiber on the working state of the laser; this laser shows clearly different dynamics from a delayed feedback laser. The laser with the physics effects of the twisted fiber will show a lot of dynamics behaviors by adjusting the control parameters. It predicts another research field of laser by introducing some physics effects to the laser system.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. The laser beats.

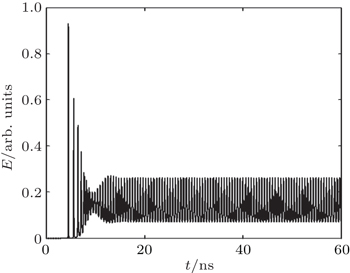
When the control parameter is taken as τ₂ = 5/3 ns, the laser is conduced to another periodic state after 60 ns, where the original periodic behavior of the laser is affected and its oscillation frequency shifts to 2.1 GHz as shown in Fig. 4. When the parameter is taken as τ₂ = 7/3 ns, the laser is conduced to another periodic state after 30 ns where the laser oscillation frequency is 2.2 GHz as illustrated in Fig. 5. When we take the parameter τ₂ = 55/30 ns, the laser shows a cycle-8 (Fig. 6). By taking τ₂ = 56/30 ns, the laser is controlled to a cycle-9 as shown in Fig. 7.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The laser oscillates periodically after 60 ns.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The laser pulses periodically after 30 ns.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. A cycle-8 orbit.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. A cycle-9 orbit.

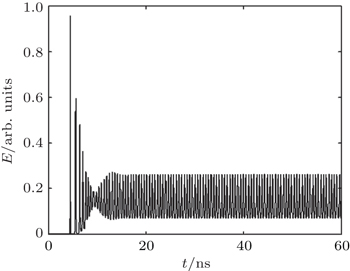
When we change the parameters to ξ = 1 rad/m and τ₂ = 5/3 ns, the laser is controlled to a stable state after 50 ns as shown in Fig. 8. When the parameter τ₂ = 4/3 ns, the laser is conduced to a double-cycle as shown in Fig. 9.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. The laser will output stably after 50 ns.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. A double-cycle orbit.

When we take the parameters Δβ = 100 rad/m, ξ = 3 rad/m, and τ₂ = 5/3 ns, the laser is controlled to a cycle-6 as shown in Fig. 10.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. A cycle-6 orbit.

When we take the parameters Δβ = 160 rad/m, ξ = 4 rad/m, r₂ = 0.02, and τ₂ = 45/30 ns, the laser is suppressed to a stable state after 25 ns as illustrated in Fig. 11. When τ₂ = 5 ns, the laser shows chaos. The chaotic attractor and the enhanced spectrum width are shown in Figs. 12(a) and 12(b), respectively. It implies that the laser is anti-controlled to chaos. When we take τ₂ = 5/3 ns, the laser is conduced to a single-periodic state after 30 ns (Fig.13), and the laser oscillation frequency is 1.95 GHz.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. The laser is in a stable state after 25 ns.

Fig. 12.

	Figure Option ViewDownloadNew Window
	Fig. 12. (a) A typical chaotic attractor and (b) the spectrum.

Fig. 13.

	Figure Option ViewDownloadNew Window
	Fig. 13. The laser oscillates periodically after 30 ns.

We find that the laser shows many complex dynamics behaviors by changing the control parameters of the twisted fiber due to a low twisted rate. We can effectively control the laser.

The parameters of the twisted fiber can be taken as ξ = 600 rad/m, Δβ = 60 rad/m, G = 0.08 when the large twisted rate fiber is introduced to the system. Let r₂ = 0.08 and τ₂ = 45/30 ns, as shown in Fig. 14, the laser will be in a stable state after 30 ns. With τ₂ = 5/3 ns, figure 15 shows that the laser is a chaotic state. We find that the laser can be controlled to a stable state or anti-controlled to chaos. With τ₂ = 2 ns, the laser shows a periodic behavior (Fig. 16).

Fig. 14.

	Figure Option ViewDownloadNew Window
	Fig. 14. The laser evolves to a stable state after 30 ns.

Fig. 15.

	Figure Option ViewDownloadNew Window
	Fig. 15. (a) A chaotic attractor and (b) the spectrum.

Fig. 16.

	Figure Option ViewDownloadNew Window
	Fig. 16. The laser oscillates periodically after 20 ns.

When the control parameters are taken as r₂ = 0.004 and τ₂ = 55/30 ns, the laser shows a period-15 in Fig. 17. With τ₂ = 3 ns, the laser shows a multi-period in Fig. 18.

Fig. 17.

	Figure Option ViewDownloadNew Window
	Fig. 17. A cycle-15 orbit.

Fig. 18.

	Figure Option ViewDownloadNew Window
	Fig. 18. A multi-period belt.

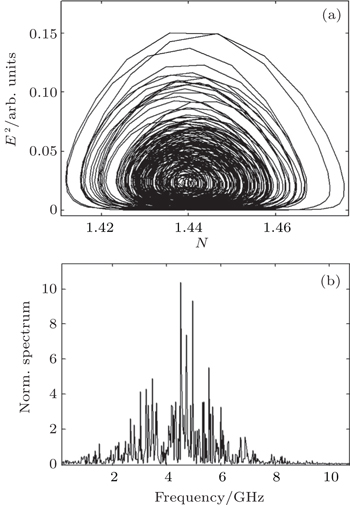
We discuss the dynamics behavior changing with the control parameter τ₂ to show a road to chaos. Let r₂ = 0.012, we find that the laser is in a period state at a frequency of 2 GHz when τ₂ = 1.5 ns. When τ₂ = 5/3 ns, the laser will operate at a stable state after 20 ns (Fig. 19). Increasing τ₂ to 55/30 ns, the laser will be in another stable state. When τ₂ = 2 ns, the laser is in another period state at a frequency of 1.9 GHz. Increasing τ₂ to 65/30 ns, we find that the laser has a multi-period (Fig. 20). With τ₂ = 1.4 ns, the laser shows a period-15 in Fig. 21. When τ₂ = 8/3 ns, we find that the laser is in a period state at a frequency of 1.8 GHz. We find that the laser can be anti-controlled to chaos when the parameter τ₂ is taken from 85/30 ns to 5 ns. Figures 22(a) and 22(b) show the chaotic behavior of the laser when τ₂ = 85/30 ns. The above results describe roughly a road to chaos from a stable state after some diverse multi-period.

Fig. 19.

	Figure Option ViewDownloadNew Window
	Fig. 19. The laser is controlled to a stable state after 20 ns.

Fig. 20.

	Figure Option ViewDownloadNew Window
	Fig. 20. Another multi-period belt.

Figure 23(a) gives the operating state of the system as a delayed dual-feedback laser without considering any effects of Δβ, R, and Ω of the twisted fiber feedback loop, where τ₁ = 1 ns, r₁ = 0.006, τ₂ = 1.1 ns, and r₂ = 0.008. Figure 23(b) gives the operating state of the system considering the effects of the twisted fiber feedback loop, where τ₁ = 1 ns, r₁ = 0.006, τ₂ = 1.1 ns, r₂ = 0.008, ξ = 600 rad/m, Δβ = 60 rad/m, and G = 0.08. A comparison of Figs. 23(a) and 23(b) indicates that the function or effect of the twisted fiber on the behavior of the laser is obvious and the laser system shows clearly different dynamics from a delayed dual-feedback laser.

Fig. 21.

	Figure Option ViewDownloadNew Window
	Fig. 21. Another period-15.

Fig. 22.

	Figure Option ViewDownloadNew Window
	Fig. 22. The laser is anti-controlled to chaos: (a) chaotic attractor and (b) spectrum.

Fig. 23.

	Figure Option ViewDownloadNew Window
	Fig. 23. The laser is stabilized in panel (a), while the laser is anti-controlled to chaos in panel (b).

We present a novel semiconductor laser system with a twisted fiber. We study the dynamics behaviors, period-control, and chaos-anti-control of the laser system. The laser is conduced to a stable state, a single-period, a double-period, a period-6, a period-8, a period-9, a multi-period state, beat phenomenon, and so on. The laser can be anti-controlled to chaos. We also give a rough road to chaos.

We find that the laser shows many complex dynamics behaviors by changing the twisted fiber parameters. The laser shows complex dynamics through a road to chaos from a stable state by changing the twisted fiber parameters because the birefringence, phase delay, and rotation of the twisted fiber vary with the fiber length. Our numerical results also show that the large Δβ obviously affects the laser behavior when ξ ≪ Δβ and the high ξ results in behavior variety of the laser when ξ ≫ Δβ. By introducing some physics effects to innovate on laser or control chaos, it is a new research method and is very useful for the study of chaos-control, new laser systems, and other nonlinear systems and their applications.