† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
A new synchronization scheme for chaotic (hyperchaotic) maps with different dimensions is presented. Specifically, given a drive system map with dimension n and a response system with dimension m, the proposed approach enables each drive system state to be synchronized with a linear response combination of the response system states. The method, based on the Lyapunov stability theory and the pole placement technique, presents some useful features: (i) it enables synchronization to be achieved for both cases of n < m and n > m; (ii) it is rigorous, being based on theorems; (iii) it can be readily applied to any chaotic (hyperchaotic) maps defined to date. Finally, the capability of the approach is illustrated by synchronization examples between the two-dimensional Hénon map (as the drive system) and the three-dimensional hyperchaotic Wang map (as the response system), and the three-dimensional Hénon-like map (as the drive system) and the two-dimensional Lorenz discrete-time system (as the response system).
The topic of controlling a chaotic drive system and a driven (response) system to get synchronized dynamics has attracted great interest in nonlinear science.[1–31] Most of the methods that have been inspired by the Carroll and Pecora work[1] focus on complete (identical) synchronization, where two identical chaotic systems asymptotically approach the same trajectory.[2–6] Subsequently, different types of synchronization have been proposed in the literature.[8–10] Among them, the projective synchronization provides response system variables that are scaled replicas of the drive system variables.[7,8] Since the scaling factor is not predictable in Ref. [7], control methods have been successively developed for choosing any desired scaling factor.[8–13] A variation of projective synchronization is the so-called full state hybrid projective synchronization (FSHPS).[14–18] In this type of synchronization, the scaling factor can be different for each state variable, meaning that the single scaling parameter originally introduced in Ref. [7] is replaced by a diagonal scaling matrix. Recently, an interesting scheme[19] has been introduced, in which each response system state achieves synchronization with any arbitrary linear combination of drive system states. Since the adoption of an arbitrary scaling matrix represents a generalization of FSHPS (where the scaling matrix is a diagonal one), the method in Ref. [19] has been called arbitrary full-state hybrid projective synchronization (arbitrary FSHPS).
Based on these considerations, this paper presents a new synchronization scheme, with which each drive system state synchronizes with a linear combination of response system states. Since the drive system states and the response system states are inverted with respect to the arbitrary FSHPS, the proposed scheme is called inverse full-state hybrid projective synchronization (IFSHPS). The approach presents some useful features: (i) it enables chaotic (hyperchaotic) maps with different dimensions to be synchronized; (ii) it is rigorous, being based on theorems; (iii) it can be applied to a wide class of chaotic (hyperchaotic) maps.
The paper is organized as follows. In Section 2, the definition of inverse full state hybrid projective synchronization is introduced. In Section 3, two theorems are proved, which enable synchronization between n-dimensional and m-dimensional maps to be achieved for the n < m and n > m cases, respectively. Finally, the capability of the method is illustrated by examples of IFSHPS between the two-dimensional Hénon map (as the drive system) and the three-dimensional hyperchaotic Wang map (as the response system), and the three-dimensional Hénon-like map (as the drive system) and the two dimensional Lorenz discrete-time system (as the response system).
It is assumed that the drive and response chaotic (hyperchaotic) systems considered herein can be written, respectively, in the form
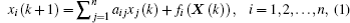
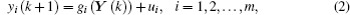
The definition of inverse full-state hybrid projective synchronization for the coupled chaotic systems given in Eqs. (
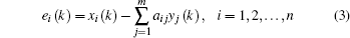
The error system (
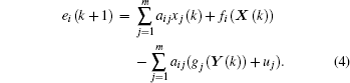
In this case, the error system described by Eq. (
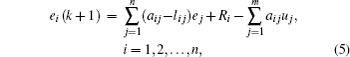

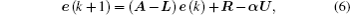
In order to achieve IFSHPS between systems (
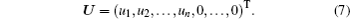
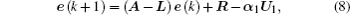
(
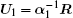
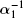
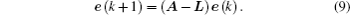
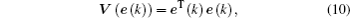
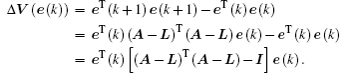
Now, the error system between the drive system (
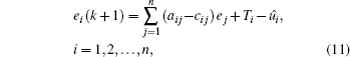
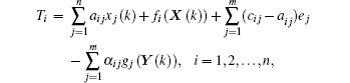

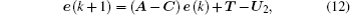
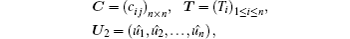
all eigenvalues of
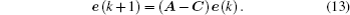
In this section, two examples are used to show the effectiveness of the proposed approach.
Herein, the chaotic two-dimensional Hénon map is selected as the drive system and the hyperchaotic three-dimensional Wang system is chosen as the response system. The Hénon map[32] is described by
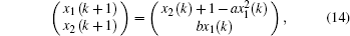
System (
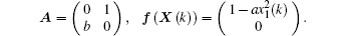

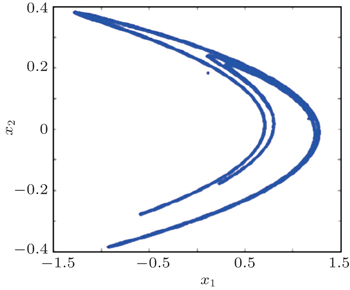
 | Fig. 2. Hyperchaotic attractor of the Wang system when (a1, a2, a3, a4, a5, a6, a7) = (1.9, 0.2, 0.5, 2.3, 2, 0.6, 1.9, 1). |
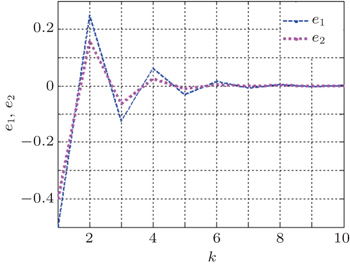
In this example, according to Eq. (
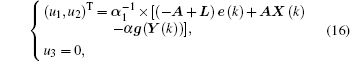

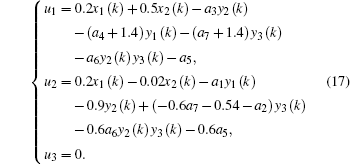

Now, the hyperchaotic three-dimensional Hénon-like map is selected as the drive system and the chaotic two-dimensional Lorenz discrete-time system is chosen as the response system. The three-dimensional Hénon-like map[34] is described by

System (
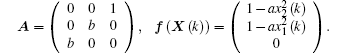
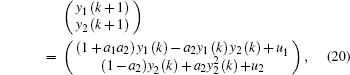
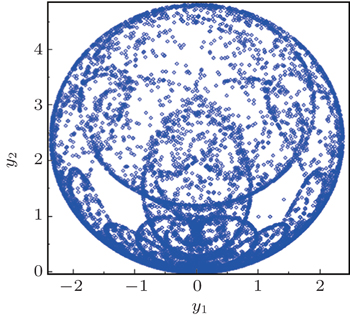 | Fig. 5. Chaotic attractor of the Lorenz discrete-time system in the (y1, y2)) plane when (a1, a2) = (1.25, 0.75). |
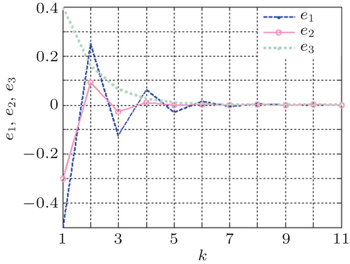
In this example, the scaling constant matrix
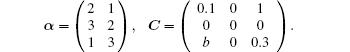

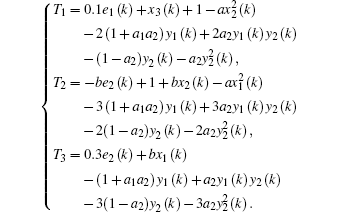
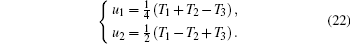

Referring to chaotic discrete-time systems, herein comparisons are carried out between the proposed approach and a number of synchronization methods in the literature, with the aim to show the advantages and the novelty of the conceived scheme.
In Ref. [27], attention was mainly focused on the full-state hybrid projective synchronization and related issues, with application to 2D discrete-time systems. Even though the theoretical approach developed in Ref. [27] is interesting, being based on nonlinear control method and Lyapunov stability, the proofs of the synchronization schemes are limited to 2D discrete-time systems only. This is further confirmed by simulation results, which focus on 2D systems only, i.e., the Fold discrete-time system (drive system) and the Lorenz discrete-time system (response system), which are both two-dimensional systems.[27] On the other hand, the technique proposed herein enables inverse full-state hybrid projective synchronization to be achieved for n-dimensional drive systems and m-dimensional response systems. As a consequence, the approach developed herein is much more general than the one illustrated in Ref. [27].
In Ref. [28], the issue of generalized synchronization (GS), along with its inverse problem, was discussed with reference to discrete-time systems. In GS, two chaotic systems are said to be synchronized if there exists a functional relationship Φ between the drive system states and the response system states.[28] However, the synchronization schemes discussed in Ref. [28] are very different from those proposed herein. Namely, in this paper, we do not consider any functional relationship Φ between drive and response systems. According to the IFSHPS schemes developed herein, each n-dimensional drive system state synchronizes with a linear combination of m-dimensional response system states. This holds for both cases of n < m and m > n.
Finally, in Ref. [29], the problem of inverse matrix projective synchronization (IMPS) for different dimensional chaotic systems in discrete-time was investigated. In this type of synchronization, the drive system and the response system synchronize up to a special scaling matrix, as shown through the examples reported in Ref. [29]. It can be argued that, while the synchronization criteria reported in Ref. [29] are restricted to specific scaling matrices, in this paper a general IFSHPS approach is developed, where each drive system state synchronizes with any arbitrary linear combination of response system states. In conclusion, the approach developed herein is much more general than the one illustrated in Ref. [29], since arbitrary scaling matrices can be exploited to achieve IFSHPS.
We have illustrated a new scheme to achieve chaos (hyperchaos) synchronization in discrete-time between a drive system of dimension n and a response system of dimension m. The proposed approach, which enables each drive system state to be synchronized with a linear response combination of response system states, has shown some remarkable features. Namely, by exploiting the Lyapunov stability theory and the pole placement technique, synchronization is rigorously proved to be achievable for any chaotic (hyperchaotic) map defined to date, including the two cases n < m and n > m. Finally, the effectiveness of the method has been illustrated by synchronizing a two-dimensional chaotic Hénon map with a three-dimensional hyperchaotic Wang map, and a three-dimensional hyperchaotic Hénon-like map with a two-dimensional chaotic discrete-time Lorenz system.