† Corresponding author. E-mail:
Project supported by the Global Change Research Program of China (Grant No. 2015CB953904), the National Natural Science Foundation of China (Grant Nos. 11275072 and 11435005), the Doctoral Program of Higher Education of China (Grant No. 20120076110024), the Network Information Physics Calculation of Basic Research Innovation Research Group of China (Grant No. 61321064), and Shanghai Collaborative Innovation Center of Trustworthy Software for Internet of Things, China (Grant No. ZF1213).
We study the generalized Darboux transformation to the three-component coupled nonlinear Schrödinger equation. First- and second-order localized waves are obtained by this technique. In first-order localized wave, we get the interactional solutions between first-order rogue wave and one-dark, one-bright soliton respectively. Meanwhile, the interactional solutions between one-breather and first-order rogue wave are also given. In second-order localized wave, one-dark-one-bright soliton together with second-order rogue wave is presented in the first component, and two-bright soliton together with second-order rogue wave are gained respectively in the other two components. Besides, we observe second-order rogue wave together with one-breather in three components. Moreover, by increasing the absolute values of two free parameters, the nonlinear waves merge with each other distinctly. These results further reveal the interesting dynamic structures of localized waves in the three-component coupled system.
In the past several years, localized waves including dark or bright soliton, breather and rogue wave have been of great interests in nonlinear science. The dark and bright soliton are special cases of soliton. The breather is localized in time or space, such as Ma breather (time-periodic breather solution)[1] and Akhmediev breather (space-periodic breather solution).[2] While the rogue wave (also called freak wave, monster wave, killer wave, rabid-dog wave, and other names) is localized in both time and space, and seems to appear from nowhere and disappear without a trace.[3–6] There have been many articles on rogue waves of single-component systems, such as the nonlinear Schrödinger (NLS) equation,[7–9] the derivative NLS equation,[10,11] the Kundu–Eckhaus equation,[12–14] the Sasa–Satsuma equqtion,[15] the higher-order dispersive NLS equation,[16] and so on.
However, a variety of complex systems,[17–19] such as Bose–Einstein condensates and nonlinear optical fibers, usually involve more than one component. So recent studies are extended to localized waves in multicomponent coupled systems, and many interesting and appealing results have been obtained. The bright–dark–rogue solution[20,21] and other higher-order localized waves[22] are all found in two-component coupled NLS equation. Some semi-rational, multi-parametric localized wave solutions are obtained in coupled Hirota equation.[23–25] A four-petaled flower structure rogue wave is exhibited in three-component coupled NLS equation.[26]
Motivated by the works of Baronio[27] and Guo,[9,28] we study the localized wave solutions of the three-component coupled NLS equation

Here we are interested in the interactional solutions between rogue waves and some nonlinear wave solutions in the Eq. (
The localized waves, such as second-order dark–bright–rogue wave and second-order breather–rogue wave, have been discussed in detail.[22,24] N-component NLS equation has been solved to get multi-dark soliton.[29] Meanwhile, performing Hirota bilinear method to Eq. (
In this section, we construct the generalized DT of Eq. (




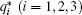
Based on the DT of the Ablowitz–Kaup–Newell–Segur (AKNS) spectral problem,[28] the generalized DT of Eq. (








Here,
We begin with the nontrivial seed solution of Eq. (
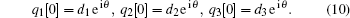
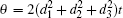



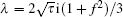











Here 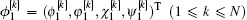







The validity of Eqs. (
 | Fig. 2. Evolution of the first-order dark–bright–rogue wave of the three-component NLS equation (a) q1, (b) q2, (c) q3 by choosing α = 1/10, β = −1/10, d1 = 1, and d2 = d3 = 0. |
 | Fig. 3. Evolution of the first-order breather–rogue wave of the three-component NLS equation (a) q1, (b) q2, (c) q3 by choosing α = 1/100, β = −1/100, d1 = 1, d2 = 1, and d3 = −0.5. |
Here, we give a classification about values of parameters α, β, and di (i = 1,2,3) corresponding to different types of first-order local wave solutions.
| Table 1. Classification of first-order local wave solutions generated by the first-step generalized DT. . |
| Table 2. Classification of first-order local wave solutions generated by the first-step generalized DT. . |
Next, we consider the following limit:




 | Fig. 4. Evolution of the second-order rogue wave of the three-component NLS equation (a) q1, (b) q2, (c) q3 by choosing α = 0, β = 0, d1 = 1, d2 = −1, d3 = 2, m1 = 100, and n1 = 0. |
 | Fig. 7. Evolution of the second-order dark–bright–rogue wave of the three-component NLS equation (a) q1, (b) q2, (c) q3 by choosing α = 10, β = −10, d1 = 1, d2 = 0, d3 = 0, m1 = 100, and n1 = 0. |
 | Fig. 8. Evolution of the second-order breather–rogue wave of the three-component NLS equation (a) q1, (b) q2, (c) q3 by choosing α = 1/100, β = −1/100, d1 = 1, d2 = −1, d3 = −1, m1 = 100, and n1 = 0. |
In Eq. (
We give some interesting localized waves of three-component NLS equation by the generalized Darboux transformation. With a fixed spectral parameter and a special vector solution of Lax pair of Eqs. (
We mainly discuss the dynamics of these solutions through three different cases. (i) When α = 0 and β = 0, the first- and second-order rogue wave are given, which are similar to one-component and two-component NLS equation. (ii) When α ≠ 0, β ≠ 0, d1 ≠ 0, d2 = 0, and d3 = 0, the first-order one-dark-rogue and one-bright-rogue wave can be gained. Meanwhile, the second-order one-dark-one-bright-rogue wave and two-bright-rogue wave are also presented. The parameter s1 determines the shape of rogue wave, such as fundamental pattern and triangular pattern. (iii) When α ≠ 0, β ≠ 0, and di ≠ 0 (i = 1,2,3), the first- and second-order one-breather–rogue wave are observed.[36] With increasing the absolute values of α and β, we can observe that rogue wave and those other nonlinear waves merge distinctly.
The localized waves of three-component coupled NLS equation are not absolutely identical with ones of two-component coupled NLS equation.[22] Second-order one-dark-one-bright-rogue wave can be obtained in q[1] component, instead of second-order two-dark-rogue wave in the two-component case. Furthermore, we get second-order rogue wave which contains four fundamental ones and this type of rogue wave interacts with one-dark-one-bright soliton, which is different with the case of two-component. We can only get one-breather–rogue wave solution, which is not the two-breather–rogue wave ones in two-component NLS equation. Through considering both two-component and three-component NLS equation, we may well understand the localized waves of the multi-component NLS equation.[37]
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 |





