† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 50478088) and the Natural Science Foundation of Hebei Province, China (Grant No. E2015202266).
Based on the symmetric two-lane Nagel–Schreckenberg (STNS) model, a three-lane cellular automaton model between two intersections containing a bus stop with left-turning buses is established in which model the occurrences of vehicle accidents are taken into account. The characteristics of traffic flows with different ratios of left-turn lines are discussed via the simulation experiments. The results indicate that the left-turn lines have more negative effects on capacity, accident rate as well as delay if the stop is located close to the intersections, where the negative effect in a near-side stop is more severe than that in a far-side one. The range of appropriate position for a bus stop without the bottleneck effect becomes more and more narrow with the increase of the ratio of left-turn bus lines. When the inflow is small, a short signal cycle and a reasonable offset are beneficial. When the inflow reaches or exceeds the capacity, a longer signal cycle is helpful. But if the stop position is inappropriate, the increase of cycle fails in reducing the negative effect of left-turning buses and the effectiveness of offset is weakened.
As an important part of public transport networks, bus stops provide the basic conditions for the buses to load and unload passengers.[1] They are crucial for urban public transport. However, the set bus stops have some negative influence on road traffic systems.[2,3] The traffic flow on a roadway is affected when a bus enters in and departs from a stop, for the driving behaviors of other vehicles near the bus have to be changed. Inappropriate position for a bus stop, especially located close to an intersection, magnifies the negative influence, which frequently causes traffic congestion and acts as a bottleneck for the road.[2–8] Moreover the road capacity drops and some traffic accidents may happen. These have been proved by plenty of theoretical studies about the influence of bus stops for roadway traffic and engineering practice, particularly by using the cellular automata (CA) model in the last decade, which is discrete in both space and time.[2–8] For instance, the capacity-drop phenomenon was analyzed, and the combined effect of the signalized intersections and its near-by bus stops was discussed by using a two-lane CA model by Song and Zhao,[2] and Zhao et al.[5,6] Qian et al. studied the influences of public transit and the harbor-shaped bus stop on traffic flow by using a one-lane CA traffic model.[9] Tian investigated lane-changing and dwelling behaviors in a two-lane mixed traffic for different proportions of buses over the whole flow.[8] According to Kinematic wave theory,[10] Gu et al. developed models and studied vehicle delays and optimization measures when a bus stop was located at a short distance from a signalized intersection.[3,4] These studies lay the foundation for further studying the influence of bus stops. However, there are some limitations.
Firstly, the case in which the bus stop has left-turn lines has not been studied, and the influence of left-turning buses has not been discussed either.[3–8] In fact, left-turning buses have to change lanes to the left-turn lane after they have departed from the stop and before they reach the forbidden lane-changing segment at the downstream intersection. Conflicts between left-turning buses and through or right-turning vehicles may occur if the road length for left-turning buses is short and the flux is large with a long queue. This is the main reason why traffic congestion happens and makes the segment a bottleneck, thereby triggering possible traffic accidents.
Secondly, the occurrence of vehicle accident has not been discussed in these models. All drivers are rational, and the safety distance can be met at all times, which does not conform to the actual road traffic case obviously.[11–16] Especially when a left-turning bus changes lane to the left-turn lane after it has departed from the stop, the through or right-turning vehicles at a relatively high speed might collide with it.[13–15] As a result, a rear-end accident may occur.
Thirdly, the coordinated signal timing scheme between two intersections has not been studied. Although some researches discussed that the capacity can be maximized by adjusting both the stop position and the cycle, the influence of offset between the two intersections has not been involved.
According to these concerns, we extend the research object to a road between two signalized intersections containing a bus stop with left-turn lines. A three-lane CA model with the detailed lane-changing rules is presented, where vehicle accidents occur when the necessary conditions are satisfied simultaneously. The influences of bus stop position on capacity, accident rate, and delay are discussed and the performances of cycle time and offset between two intersections are analyzed.
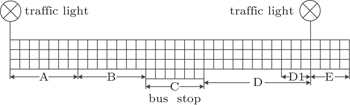
As shown in Fig.
In order to describe the traffic flow processing of the studied object, we establish an extended three-lane CA model based on a symmetric two-lane Nagel–Schreckenberg (STNS) model with taking into account the occurrences of vehicle accidents. The road is divided into cells. The length of each cell is 1 m for the purpose of simulating the lane-changing behaviors in a more precise way. Each cell may be either empty or occupied by one vehicle with an integer velocity v between zero and the maximal speed limit vmax, where we use vmax1 in place of vmax for a car and vmax2 in place of vmax for a bus. x(i, t) and v(i, t) denote the position and velocity of vehicle i at discrete time step t, respectively. The first vehicle is numbered as 1, and the following vehicles as 2, 3, …, i. Here d(i, t) = x(i, t) − x(i − 1, t) − l is the empty cells between vehicle i and its predecessor at time t, with l representing the number of cells occupied by one vehicle where l is 6 for a car and 12 for a bus, d(i, t)front and d(i, t)back denoting the empty cells between vehicle i and its predecessor and its successor on its destination lane, respectively. Let dsafe denote the safe distance between a vehicle and its preceding one. Considering the complexity of the studied problem, we set dsafe to be vmax in normal vehicle driving motion, and to be 1 m if the speed of the predecessor is zero and the vehicle has to queue for waiting. If the leading vehicle in each lane before the downstream intersection is vehicle i and the signal light of its direction is red, the gap will be calculated as d(i, t) = xlight − x(i, t), where xlight is the position of the stop line at the downstream intersection.
At each discrete time step t → t + 1, the system is updated by the following rules.
In normal lane-changing rules of a CA mode for a vehicle, the lane-changing probability P is set as a fixed value. But in the study, only partial lane-changing probability with a fixed value is used.[17–19] Here PLC and PRC denote the probabilities for a car changing to its left-side lane and changing to its right-side lane if the lane-changing rules are met, respectively. PLB and PRB denote the probabilities for a bus changing to its left-side lane and changing to its right-side lane if the lane-changing rules are met, respectively.
The different lane-changing rules of a vehicle in different segments are as follows.
The maximal velocity of bus in the stop is set to be vmax22, and vmax22 < vmax2. The rules for a bus to enter into, move forward and depart from the stop are described in Subsection 2.2. It is impossible to overtake for there is only one lane. When a bus stops in the stop, meaning that its speed is zero, its dwelling time Ts is generated randomly, which follows a normal distribution with a mean value of 30 s according to the Transit Co-operative Research Program (TCRP) Report 19(1996).[5,6]
The coordinated signal timing schemes with four-phase are used, where T is the cycle time and G is offset between the two intersections. For each intersection, the timing scheme includes through and right-turn phase with green time TTR1 and left-turn phase with green time TL1 in the east–west direction, through and right-turn phase with green time TTR2 and left-turn phase with green time TL2 in the north–south direction.
Considering that the conditions of traffic accidents proposed by Boccara et al.,[13] are applied to the continuous traffic flow road, on which a vehicle can move at a high speed and the gap between two vehicles is large, we adjust the first condition d(i, t) ≤ vmax to d(i, t) ≤ v(i, t) for the reality of urban roads with a low speed and small gap. The other conditions of Boccara et al. remain unchanged.[13] The modified conditions are as follows.
If the three conditions are met, a rear-end accident or a conflict is calculated. Obviously the above three conditions for the occurrences of car accidents hold true under the assumption of neglecting time correlations.[13] Although the future traffic state, i.e., v(i + 1, t + 1), cannot be known at current time in real traffic, the accident rate in the numerical simulation can be calculated when the simulation is all finished, which means that we have obtained all the sequences of space and time data and know all the states in the simulation period. Here the accident rate is just a numerical parameter in evaluating the influence on traffic safety.
The accident occurrence number Nac is increased by 1 if these necessary conditions are satisfied. The accident probability Pac is defined as Nac/N, where N is the total number of vehicles.
A statistical approach is proposed to calculate the delays experienced by vehicles, including average control delay and delay incurred by bus interference near the stop. Specifically, it is assumed that the cars would travel through the road with maximal speed vmax in the absence of a control facility of the intersection. At each time step, vehicles move forward a length of current speed v, thus we calculate the difference between speed v and vmax at each time step for each vehicle on the road in the stimulation period TT. The delay D is defined as
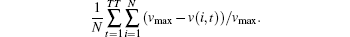
The boundary conditions are open.
The vehicles generated randomly on the stop lines of the upstream intersection pass through the intersection according to the signal control rules, where partial vehicles reach Segment A and become the real inflow of the studied object. In order to simplify the studied problem, the signalized intersections are not included into the studied object. But we use some relatively simple rules to map the relation between the signal control rules of the upstream intersection and the inletting flow. In each green-light period, the total entering probability is distributed to each lane of the subject street segment. Pe denotes the entering probability for each inletting lane of the upstream intersection. Values of 20 percent for right turns and 20 percent for left turns are assumed to be a percentage of the total approaching traffic in each cycle time T in this model. Let t1, t2, t3, t4, and t5 denote the travel times of vehicles on the eastbound through lane, eastbound through and right-turn lane, westbound left-turn lane, northbound through and right-turn lane, southbound left-turn lane from their stop lines of the upstream intersection to Segment A if the signal lights of their directions are green, respectively. Obviously the inflow in Segment A that does not possess the characteristics of continuous traffic flow consists of the vehicles from the five lanes after ti time delayed and corresponding to signal lights.
At each time step, the leading vehicle in each lane of the downstream intersection is removed, if its position xfirst > LR. Here LR denotes the length of the road. Then its following vehicle becomes the new leader.
The road described in Section 2 is simulated, where the total length LR is 1200 m meaning that there are 1200 cells and the downstream intersection is located at the 1000th cell. Section C contains LC = 50 cells, section D1 contains LD1 = 30 cells, and section E contains LE = 200 cells. L denotes the distance between the stop and the downstream intersection. The ratio of the left-turning car is 0.2. Four bus lines are set. Other parameters are set as follows: vmax1 = 14, vmax2 = 11, vmax22 = 5, P1 = P2 = 0.3, PLC = PRC = x(i, t)/(1000 − LD1), t1 = t2 = 5 s, t3 = 3 s, t4 = 4 s, t5 = 6 s. PLT = PRT = 0.2, and PLU = 0.01. Bus arrival follows a Poisson distribution and the average arrival rate is 1/60. Each time step corresponds to 1 s. The first 104 time steps are eliminated to avoid transient behaviors. The flow is averaged by 2×104 time steps. The final result is an average of 10 simulation results in order to reduce stochastic influence.
The coordinated signal timing schemes with four phases are used. The control parameters of the two intersections are set to be the same, for there is no difference in basic condition between the intersections. At the same time, we adopt different timing strategies by the traffic states in order to obtain the optimal control parameters. The fixed timing control is used for saturated flow, and actuated signal control is used for unsaturated flow.[20] Then the concrete control method and parameters are optimized for each simulation experiment. For example, three methods including the most famous and typical TRRL (Webster) model and its two improved methods, namely the Australian Road Research Bureau (ARRB) model and the stop-line method, are used to calculate the parameters of each signal timing scheme when the traffic state is saturated flow.[18–20] By comparing the simulation results of signal timing schemes, the method and its parameter values are determined. Table
| Table 1. Comparison among three timing methods. . |
Figure
In order to fully understand these negative effects of left-turn buses, figure
The relations between the capacity and L, Pac, and L with the different ratios of left-turning bus lines are shown in Figs.
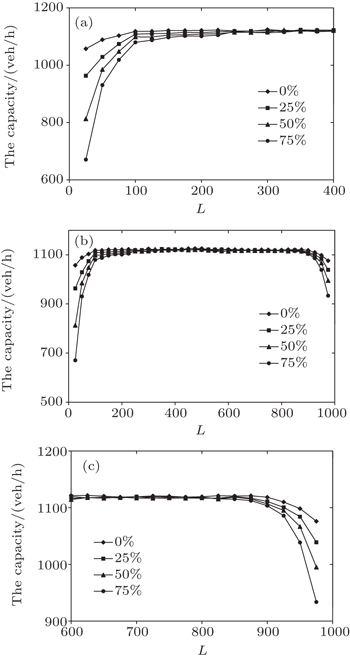 | Fig. 4. Relationships between the capacity and L for different ratios of left-turn bus lines with values of L being in the ranges [0,400] (a), [0,1000] (b), and [600,1000] (c). |
 | Fig. 5. Relationships between Pac and L for different ratios of left-turn bus lines with the values of L being in the ranges [0,400] (a), [0,1000] (b), and [600,1000] (c). |
Figure
At the same time, the area of region II with no left-turn bus line is smaller than that with 2 left-turn bus lines. The area of region III with no left-turn bus line is larger than that with 2 left-turn bus lines. This is because the negative effects caused by left-turning buses are more serious if the stop is close to the intersection. With the increase of the left-turn bus lines, LBC1 becomes large and LBC2 becomes small. The range of mediate value LBC without a bottleneck effect becomes smaller. So the area of region III becomes smaller. Moreover the expanded area of region II in the left of Fig.
Thus, for a bus stop that contains left-turn lines, a far-side stop is preferred to a near-side one, and a near-side stop should keep a longer distance from the downstream intersection to ease the negative effect caused by the left-turning bus in its lane-changing process.
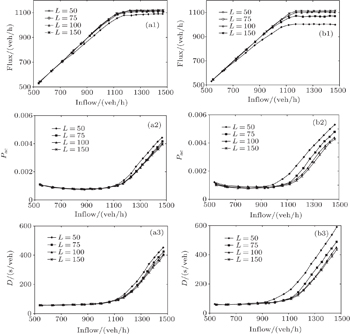
Figure
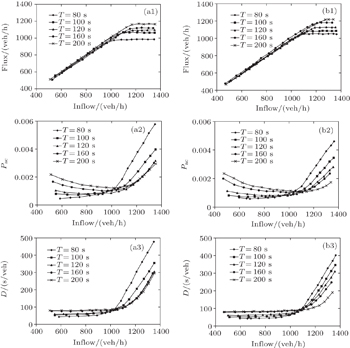 | Fig. 7. Relationships between the flux and inflow, Pac and inflow, D and inflow for different signal cycles. (a1)–(a3): L = 100 m, (b1)–(b3): L = 200 m. |
Figure
 | Fig. 8. Influences of offset between the two intersections. (a1)–(a3): L = 100 m, (b1–b3): L = 200 m. |
The influences of bus stop with left-turn lines between two adjacent signalized intersections on capacity, accident rate and delay are studied by using a three-lane CA model. The results of the simulations suggest that the left-turning buses in a near-side stop have more negative effects. The range of appropriate position for bus stop with no bottleneck effect becomes smaller and smaller with the left-turn bus lines increasing. When the inflow reaches or exceeds the capacity, a longer signal cycle is helpful. But if the stop position is inappropriate, the increase of cycle fails to reduce the negative effect of a left-turning bus and the effectiveness of offset is weakened. These findings may provide some reference values for setting bus stop and traffic management.
Some relatively simple rules are used to map the relation between the signal control rules of the upstream intersection and the inletting flow. The inflows from different directions are set to be the same. Vehicle accident does not really occur in the simulation and these dangerous situations are only calculated and considered to be the signals of accidents occurring. Future work will concentrate on these problems.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 |