† Corresponding author. E-mail:
The quantum entanglement between two spins in the Ising model with an added Dzyaloshinsky–Moriya (DM) interaction and in the presence of the transverse magnetic field is studied. The exchange interaction is considered as a function of the distance between spins. The negativity as a function of magnetic field, exchange and DM interaction is calculated. The effect of the distance between spins is studied based on the negativity. In addition, the effect of the thermal fluctuation on the negativity is also investigated.
Quantum entanglement plays an important role in quantum information processing,[1,2] teleportation,[3] communication systems,[4–6] quantum computers,[7–9] quantum spin networks,[10] and security cryptography.[11] It has achieved many successes both in theory and experiment. Specially, it is known that the particles can be entangled in a system with long range interactions.[12,13]
Significant research has been performed to understand the quantum entanglements in different spin systems, such as XY,[14–16] XX,[17] XXZ,[18] XYZ models.[19,20] The effects of Dzyaloshinsky–Moriya (DM) interaction[21–25] and magnetic field[14,26–29] on the quantum entanglement are also studied. Negativity and its cocurrence are the most widely used measures in entanglement study. The negativity was first used by Zyczkowski et al.[30] and subsequently introduced as an entanglement measure by Vidal and Werner.[31]
In recent years, long range interactions have attracted a great deal of attention since they can produce interesting new phenomena.[32–36] A new type of long-range interaction has been introduced in Ref. [37], where the exchange interaction is inversely proportional to the power of the distance between the two spins. In 2014, it was observed that interactions in natural systems may fall into a class of long range interaction.[38] In Ref. [39], a region of logarithmic growth of entropy in a system with long-range interaction was reported. In Ref. [40], a local quench long-range Ising model in the transverse field with the resulting spread of quasi-particles was analyzed.
In the present study, we employ the negativity to analyze the entanglement in a spin system with long-range interactions. The considered model is the one-dimensional (1D) Ising model in the presence of a transverse magnetic field (ITF model) and the DM interaction. We consider the exchange interaction as a function of the distance between spins. Recently, the entanglement was studied by using this model in the case of constant exchange interaction.[41] Here, we consider exchange interaction proportional to the inverse square of distance between spins, R. We calculate the negativity and analyze the behavior of the entanglement as a function of R. Results show that the quantum correlations are very sensitive to the mutual effects of the distance and the DM interaction.
Here, we consider a set of two localized spin-1/2 particles coupled through the exchange J(R) and the DM interactions, subjected to an external magnetic field h
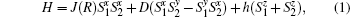
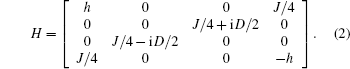
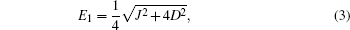
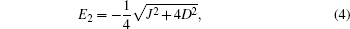
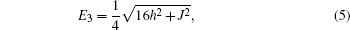
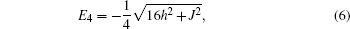
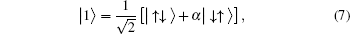
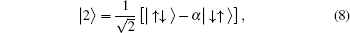
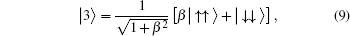
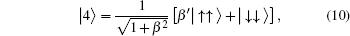

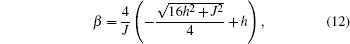
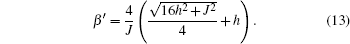
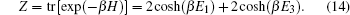
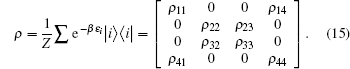
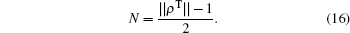
From the previous section, we can easily find the negativity. Here, we consider the exchange interaction as an inverse square function of the distance between spins, = J0/R2. For simplicity, J=1 is considered. Using Eqs. (
First, in the absence of the magnetic field nor the DM interaction, the effect of distance between two spins on their quantum entanglement is investigated. In this situation, the ground state energy is degenerated twice and corresponding eigenstates are
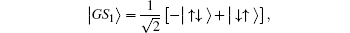

Then, we apply the DM interaction (the magnetic field yet is zero). Figure
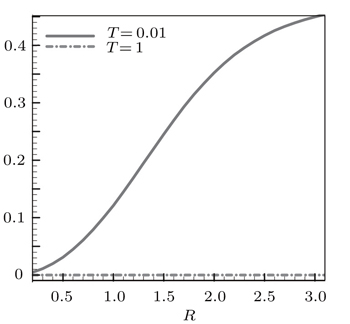 | Fig. 1. Plots of negativity versus R for the two-spin system with exchange interaction 1/R2 at two different temperatures. |
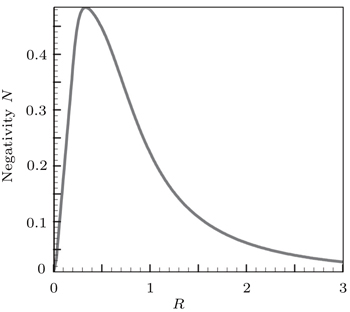 | Fig. 2. Negativity as a function of R for the two-spin system with exchange interaction 1/R2. Here, D = 0.1, h = 0.5, and T ∼ 0. |
In Fig.
If a magnetic field is applied, the dependence of the negativity on the distance for values of magnetic field less than the DM interaction will be different from that for values of magnetic field larger values of DM.
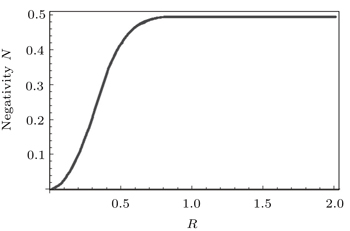 | Fig. 3. Negativity as a function of R for the two-spin system with exchange interaction 1/R2. Here, D = 0.6, h = 0.2, and T ∼ 0. |
Figure
 | Fig. 4. Magnetic field dependence of negativity N for the two-spin system with exchange interaction 1/R2. Here, D = 2, R = 0.5, and T ∼ 0. |
The study of the effect of the magnetic field on the entanglement is significant because it represents a critical magnetic field hc = D/2. In fact, at this point the ground state of the system is degenerated. For h < hc, the energy of the ground state of the system is
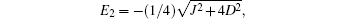

In this work, we studied the quantum entanglement between two spins in the Ising model with the addition of the Dzyaloshinsky–Moriya (DM) interaction and a transverse magnetic field. We considered the exchange interaction as an inverse square function of the distance between spins (R). Also we focused on the negativity to investigate the entanglement between spins. Our results show that spins are unentangled in the absence of the DM interaction nor the magnetic field and by adding the DM interaction, the system remains unentangled for a short distance. When we increase the distance between spins, the entanglement is induced due to the quantum effect of the DM interaction. In the presence of the magnetic field, the entanglement will be changed and in a critical field the entanglement will be zero.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 |


