† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11004082 and 11291240477), the Natural Science Foundation of Guangdong Province, China (Grant No. 2014A030313367), and the Fundamental Research Funds for the Central Universities, Jinan University (Grant No. 11614341).
Using non-equilibrium molecular dynamics and Monte Carlo methods, we study the collective diffusion of helium in carbon nanotubes. The results show that the collective diffusion coefficient (CDC) increases with the dimension of the channel. The collective diffusion coefficient has a linear relationship with the temperature and the concentration. There exist a ballistic transport in short carbon nanotubes and a diffusive transport in long carbon nanotubes. Fick’s law has an invalid region in the nanoscale channel.
Fourier’s law and Fick’s law are two important laws describing the thermal and mass transport in nature. When the dimension of the physical structure approximates to the mean free path of the carrier or the duration of the physical process is shorter than the relaxation time of the carrier, Fourier’s law cannot describe some thermal behaviors correctly in microscopic systems.[1] Similarly, it is reported when the mean free path of the carrier is far shorter than the size of the channel’s structure, Fick’s law cannot describe collective diffusion very well either.[2]
Recently, many theoretical and experimental investigations about Fick’s law and the related diffusion behavior have been extensively performed. In 1991, Alley and Alder[3] took into account the effect of time memory and proposed that Fick’s law should be improved. Later on, Brogioli and Availati[4] put forward that the local density and the fluctuation of the velocity might affect the feasibility of Fick’s law and provided a revised formula. In 1995, Cracknel et al.[5] constructed the three-dimensional (3D) box of nanoscale and studied the non-equilibrium system of particles with the concentration gradient. Through the calculation of the relation between mass flow and the concentration gradient of the particles, they found that Fick’s law was still applicable. In 2006, Haibin Chen et al.[6] studied the transport diffusions of gases in flexible carbon nanotubes and found that the transport diffusivities are still large in flexible carbon nanotubes compared with those of other materials. In the same year, Arora and Sandier[7] proposed that they used single wall carbon nanotubes to separate air. They found that good kinetic selectivity can be achieved for air separation by fine-tuning the upstream and downstream pressures. In 2010, Malek and Sahimi[8] used silicon–carbide nanotubes to study the molecular dynamics simulations of adsorption and diffusion of gases. In 2011, Liu et al.[9] came up with an efficient method to compute Fick’s diffusivities from equilibrium molecular dynamics (MD) simulations, the method does not need additional knowledge such as the equation of state of the system. In 2013, Noy[10] studied the kinetic model of gas transport in carbon nanotube (CNT) channels. It should be noted that in the same year, Becker et al.[11] proposed the correlation between the self-diffusion constant of interacting particles and the diffusion coefficient of Fick’s Law through the investigation of the hybrid behavior of two mixed gases. It was explained by the difference between transport diffusion and self-diffusion. It was declared that the transport diffusion has more physical meanings than the self-diffusion. Apart from the theoretical studies, many experimental researches have addressed the transport behaviors of molecular sieves,[12–14] biological channels,[15,16] porous medium,[17–20] etc., and further explanations of the microscopic mechanisms have been proposed. Liu and Zhu[21] studied the diffusion model for ion conduction with micro-channel and found that channel charges play a key role in current rectification rather than geometric asymmetry. In 2015, Siems and Nielaba[22] studied the diffusion model of colloidal particles with a periodic potential in a two-dimensional (2D) microscopic system. Wen et al. reported the shape-dependence of the channel on the transport diffusion.[23] All these studies above still unsettled the question on the physical mechanism of collective diffusion in nanoscale channels. Especially, it is still not clear how the collective diffusion changes when the channel crosses from one-dimensional (1D) to 3D system. In other words, it is unknown whether Fick’s Law is still valid in a nanoscale.
In this work, we will investigate the collective diffusion behavior from 1D to 3D system. Since CNTs with different diameters and lengths can be synthesized easily, here we use CNTs to model this system. As shown in Fig.
Figure
 | Fig. 2. A channel for molecular transport. Blue particle is the helium atoms, left and right particle reservoirs are connected by the carbon nanotubes, the green wall is graphene. |
We use the Monte Carlo method to control the concentration of atoms in both atom reservoirs. When the absolute activity of the atom reservoir is less (or bigger) than the present value z, an atom will be automatically created (or annihilated). When a creation is accepted, the atom is given a velocity, selected from Maxwell–Boltzmann distribution according to the simulation temperature. Equations (
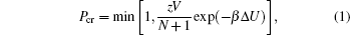
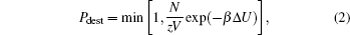
The collective diffusion coefficient is obtained from Fick’s law,
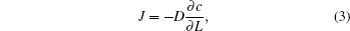
In the simulations, a non-equilibrium molecular dynamics method is used, and the two different interactions between He and He, and between He and C are described by the Lennard–Jones potential.[24] In the whole process, the positions of carbon atoms are fixed. The temperature is set according to Langevin random thermal bath. The calculus involved in the calculation is performed by the Verlet algorithm[25] in steps of 0.55 fs. In order to rapidly and accurately collect the diffusion flux, we set different stationary times depending on the length of CNTs and then calculate the unit area diffusion flux after the stationary state.
When the system transforms from 1D to 3D system, the collective diffusion behavior will be involved with the influence factors of the transport medium and the transport object. Therefore, to further analyze the nature of the molecular transport, we address the temperature, the density gradient, the chirality of the CNTs, the dimension and length of the channel.
According to Fig.
According to Fig.
As shown in Fig.
As shown in Fig.
 | Fig. 6. Length dependences of the collective diffusion constant for carbon nanotubes with different diameters. |
In the ballistic region, the shorter the transport length, the bigger the drive force of the chemical gradient ∇μ is under a fast changing nonlinear relationship, i.e., ∇μ ∝ 1/L. Usually, the numbers of atoms in the CNTs (5, 5) remarkably decreases to 1, 2, and 5 for the transport lengths of 3.49 nm, 9.15 nm, and 20.22 nm, respectively. At the same time, the average numbers of atoms in the CNTs (30, 30) are 89, 201, and 458 for the transport lengths of 3.49 nm, 9.15 nm, and 20.22 nm, respectively. Therefore, the collisions happening in short and small CNTs are less than in long and big tubes. Under the influence of the anomalous diffusion behavior, the collective diffusion constant rises up abruptly with the transport length increasing. This can be explained as follows. According to Fick’s law, the collective diffusion constant satisfies DS = JSLCNT/Δc, where the density gradient Δc is kept invariable during the simulation. Therefore, DS is closely associated only with JS and LCNT. In this phase, the anomalous diffusion behavior in the CNTs is obvious and the average speed of atoms is relatively high. Although the average number of atoms in the tubes will increase with the increase of the transport length, it will not remarkably change the value of the mass flux JS. Thus, in the simulation process, the decreasing rate of JS is lower than the increasing rate of LCNT, then the value of JSLCNT will increase constantly with the increase of the transport length. Meanwhile, the diffusion constant DS will increase with the increase of the transport length. In general, the collective diffusion constant is independent of the length, then, Fick’s law is invalid in this region.
In a diffusion region, the transport behavior possesses normal transport properties and the mass flux follows the relation of JS ∝ (LCNT)−1, which means the diffusion coefficient of DS ∝ JSLCNT remains the same. As a result, the collective diffusion coefficient is independent of the transport length and Fick’s law is valid. Comparing these two transport modes, one can observe that there is a transition point between the two transport behaviors. When the diameter of CNT increases from 0.54 nm to 4.34 nm, the length of transition point decreases from 125.97 nm to 25.14 nm. This can be explained as the fact that, within the same transport length, the atoms held by smaller tubes are less than by bigger tubes. These atoms have a more polarized direction of motion as well as more opportunities for collision. As a result, with the increase of the transport length, the collision frequency of all the atoms contained in a carbon nanotube with a large diameter is apparently higher than that with a small diameter. That is to say, within a small change of length the atoms in the large tubes can produce an obvious behavior of disordered collision and the ballistic diffusion characteristics drastically reduce to zero.
From 1D to 3D molecular transport system, the collective diffusion constant increases rapidly and finally tends to a plateau constant. The collective diffusion behavior is strongly correlated to the factors such as diameter, temperature, density gradient, transport length, etc. The higher the dimension of the system, the more strongly the temperature and density affect the collective diffusion. As the transport length increases, the transport mode changes from ballistic to normal transport. The transition point length can vary obviously for systems with different dimensions. Anyway, the transition behavior can be attributed to the existence of the anomalous diffusion behavior. The lower the dimension of the system and the shorter the transport length, the more obvious the characteristics of the super diffusion are. Our results suggest that Fick’s law may be invalid when the transport length decreases to the nanoscale region.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 |






