Ejecta produced from a shock-driven metal surface, originating from the interaction between a reflected release wave and surface defects, is an important fragmentation process in shock physics, which plays a determinative role in affecting the surface measurements and performance of inertial confinement fusion. Previous experiments^[1–10] had indicated the various factors such as surface perturbation of machined metals, material phase, and shockwave profile having a pronounced effect on the total ejected mass, the ejecta density, and velocity distributions, which are expectedly predicted by performing an ejecta term source model in hydrodynamic simulations.^[7,11] Nevertheless, there have only been a few systematic investigations of the influence of the loading shockwave profile on ejecta production in spite of its importance pointed out again in the Introduction of a recent paper.^[10]

In experiments, a supported shock having a flat top portion is created by a gas gun and an unsupported shock characterized by a decaying impulse with the time is generated by a high explosive or a pulsed laser.^[9] An unsupported shock is sometimes referred to as a Taylor or triangular wave. Experimental observations^[12,13] have shown a strong dependence of the damage evolution process on the shock loading profiles. For ejecta production,^[5,6] the total ejected mass increases linearly for a supported shock while showing a steep rise followed by a constant slope for an unsupported shock with respect to the shock-breakout pressure (P_SB) when Sn is shocked from a solid state to a mixed solid–liquid state. Several possible reasons are proposed to explain this difference, such as the time-dependent influence of the shock profile on the instability formation and micro-spall separation of layers induced by the stress state upon release at the free surface. As a helpful complement for modeling the ejecta production related to melting and damage,^[14–22] molecular dynamics (MD) simulations have been carried out to comparatively obtain the quantity of ejecta in Al for supported and unsupported shocks.^[19] The simulations exhibit a continuous increase of microjet mass with the increasing shock pressures under supported shocks and this quantity after release melting is larger than that under unsupported shocks. However, careful examination finds that the mass determination in Ref. [20] is for the jet but not for the ejected fragments. Thus, both the experimental measurements and numerically atomistic simulations cannot offer an explicit insight on the influence of shockwave shape on the ejection process, in particular regarding the quantity of the ejecta production.

The goal of the present work is to address the influence of shock wave profile on the ejection process from shocked Pb metal using MD simulation, with an emphasis on the quantity of the ejected fragments as well as the ejecta mass–velocity distribution. The total ejected masses for supported and unsupported shock waves are determined and reveal the distinct findings in contrast to the past experiments^[5,6] and simulations^[19] when Pb goes from a solid phase to a full melting phase. Moreover, we elucidate the difference by analyzing the evolution process of the ejecta produced.

The MD simulations are implemented with the free source code Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).^[23] The modeling domain filled with fcc Pb atoms is 118 × 60 × 7 nm³ with about 1.65 × 10⁶ atoms, in which surface perturbation consists of six triangular grooves calibrated with each dimension of 10 nm in height and 53.1° in groove angle. This simulated model is the same as in Ref. [20] where ejecta production under an unsupported shockwave has been examined. The X, Y, and Z axes are chosen along the [100], [010], and [001] directions, respectively. Periodic boundary conditions are imposed along the Y and Z directions, while the shock direction (X axis) is kept free. The interatomic potential for single-crystalline Pb is adopted with an embedded atom method (EAM) potential by Zhou et al.,^[24] which represents a good description of both solid and liquid phases of Pb as validated by the calculated Hugoniot pressure–temperature relation.^[25] After constructing the initial sample, the system is equilibrated through the utilization of Nose-Hoover isobaric–isothermal ensemble (NPT) with a pressure of 0 bar (1 bar = 10⁵ Pa) and a desired temperature of 100 K for 10 ps. The dynamic simulations adopt the microcanonical NVE ensemble integrating the equation of motion with a time step of 1 fs. By dividing the simulation cell into fine bins only along the shock direction (1D binning analysis) and ignoring the heterogeneities in the transverse direction, the average physical quantities are obtained in each bin, such as particle velocity and volume density. The Ovito software^[26] is employed to visualize the atomic configuration.

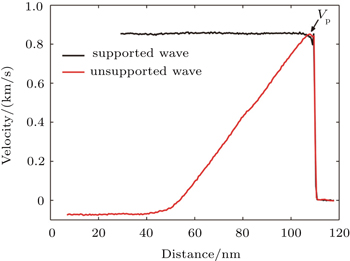
In order to generate a shock impulse, the piston by choosing the first 1 nm of the sample is given an impact velocity to drive the remaining sample. By keeping a constant velocity of the piston with a square pulse of 8 ps followed by releasing it, the rarefaction wave from the rear of the sample is formed to catch up with the shock wave. Once the release wave overtakes the shock wavefront, the unsupported shockwave profile is achieved before reflection at the groove bottom. In this case, a peak velocity denoted as V_p, is reduced in comparison to the incident loading velocity, also including a drop in peak pressure. The peak pressure is defined as the shock-breakout pressure P_SB proposed in the experimental studies,^[2,4,5] where it is worth noting that ejecta production is dependent on P_SB not the incident pressure. To quantitatively compare the results, a supported shock is generated by the piston loading with a continuous velocity equal to V_p obtained from the unsupported shocks, ensuring the same P_SB for both shocks.

Figure 1 displays the supported and unsupported shockwave profiles with the same peak velocity of V_p = 0.854 km/s when the shock wavefront arrives at the groove bottom. During the whole simulations, the peak velocity V_p spans from 0.25 km/s to 1.5 km/s, including the three states of the shocked Pb: solid, partial melting, and melting-on-shock, as also illustrated by Chen et al.^[25] Note that the arrival time of the shock wavefront on the grooved bottom shown in Fig. 1 is chosen to be the zero moment for the following discussions.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The supported and unsupported loading velocity profiles with the same peak value of Vp = 0.854 km/s before the shock wavefront reaches the groove bottom.

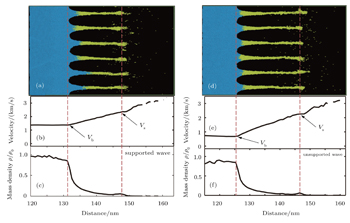
After running a long enough simulation time imposed by these two shockwaves, the ejected particles are completely broken away from the bulk, as observed from the inset of Fig. 2 for P_SB = 22 GPa where yellow and blue zones represent the ejected fragments and the bulk, respectively.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Microjetting factor R as a function of shock-breakout pressure PSB. Inset: atomic configurations for PSB = 22 GPa at t = 150 ps where yellow denotes the ejected particles and blue is for the bulk.

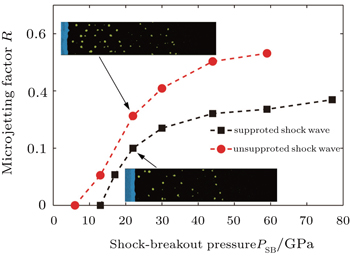
By defining the microjetting factor R as the ratio of the ejected mass to the missing mass related to the groove volume, we could obtain R as a function of P_SB for supported and unsupported shock waves, as shown in Fig. 2. With the increasing P_SB which induces the occurrence of Pb shocking to solid, releasing to liquid and shocking to liquid, R increases slowly and rises significantly followed by an approximatively flat slope for both shocks. For unsupported shocks, R qualitatively agrees with the experiments.^[4] Nevertheless, for supported shocks, the total ejected mass is always less than that for unsupported shock at the same P_SB and does not exhibit a linear relation to P_SB. This finding is completely dissimilar from the experimental one on shocked Sn targets^[5,6] imposed by a supported shockwave. From this figure, we also find that the threshold of P_SB for producing the ejecta under a supported shock is larger than that under an unsupported shock, implying that the unsupported shock induces the ejecta formation more easily.

To explicitly make the explanation for difference shown in Fig. 2, ejecta production with a peak stress of P_SB = 22 GPa (V_p = 0.67 km/s) is chosen to be analyzed, concentrating on the jetting formation at an early stage. Figure 3 exhibits the snapshots, the ejecta velocity and volume density distributions for supported and unsupported shockwaves at t = 16 ps. Note that the spatial location (X direction) of the snapshots intercepted is a one-to-one coincidence with that of the density and velocity distributions. The six jet shapes shown in Figs. 3(a) and 3(d) are similar to the numerical^[22] and experimental images.^[7,9] For the jets, there exist two important sites: the bottom, where velocity is denoted as V_b, and the tip, where velocity is marked as V_s, as are separately plotted by the dashed line in Fig. 3 for both shocks. In the volume density distributions shown in Figs. 3(c) and 3(f), they point to the turning point associated with the jump of mass density and a secondary maximum caused by minimization of surface energy, respectively. On the basis of the above definition, for supported and unsupported shocks, V_s are separately 2.31 km/s and 2.25 km/s, and V_b are separately 1.39 km/s and 0.68 km/s. In spite of the close spike velocity, the bubble velocity is in a large discrepancy, which means a larger velocity difference for unsupported shocks.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. The velocity and volume density distributions with PSB = 22 GPa are displayed for supported waves in panels (b) and (c) and unsupported waves in panels (e) and (f). The snapshots in panels (a) and (d) are the corresponding atomic images, in which yellow represents the source of the ejected particles within the jets. The dashed line separately denotes the jet bottom and its tip, where velocities are marked by Vb and Vs.

We further plot the spike and bubble velocity evolutions under these two shocks in Fig. 4. It can be seen that spike velocities of the jets are very close and slightly decrease as a function of time followed by a constant of V_s = 2.28 km/s and 2.23 km/s, respectively. The reason for a slight reduction of spike velocity is attributed to the tensile interaction within the jets and being constant arises from the jet breakup, inducing the free movement of the jet head tip. However, a difference for two shocks emerges at the bubble velocity. For the supported shock, the bubble velocity nearly keeps a constant value of V_b = 1.38 km/s, approximatively twice the peak velocity of V_p = 0.67 km/s. For the unsupported shock, however, the bubble velocity reveals a rapid drop from V_p = 1.01 km/s at t = 6 ps to V_p = 0.59 km/s at t = 36 ps, owing to the release wave interaction propagating from the backside of the sample. The small increase in the bubble velocity for the unsupported shockwave at around t = 25 ps is because the secondary reflection of shock wave occurs at the spalled layer near the free surface. The resulting velocity difference between the jet tip and its bottom at t = 36 ps is 0.9 km/s for supported shocks and 1.64 km/s for unsupported shocks. For the damage process, the velocity difference represents a state of tension and a larger value causes the damage formation more easily, which can be found about spallation damage in Ref. [13]. Thus, for jets discussed here, a larger velocity difference generates more ejecta for unsupported shocks. The yellow region in Figs. 3(a) and 3(d) displays the source of the ejected particles within the jets by tracking the ejecta in the inset of Fig. 2. Obviously the domain colored by yellow for unsupported shocks is longer than that for supported shocks.

Fig. 4.

	Figure Option ViewDownloadNew Window
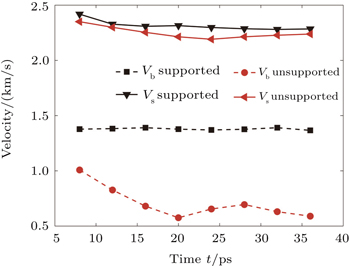	Fig. 4. The spike and bubble velocities evolution for the jets are plotted. It is evident that there exists a larger velocity difference between the jet tip and its bottom for unsupported shocks.

Actually, the above analysis could be extended for all the events displayed in Fig. 2. According to the spike velocity prediction theoretically developed by Buttler et al.^[7] and the shock-breakout pressure calculation, the spike velocity only relies on shock-breakout pressure, surface perturbation and shockwave speed at the groove bottom. Hence for jet formation under two shock conditions with the same P_SB, the spike velocities are equal. The bubble velocity for supported shocks doubles the peak velocity while for unsupported shocks it decreases rapidly due to the release wave effect. Clearly, a larger velocity difference between the jet tip and its bottom is for unsupported shocks, which ultimately produces more ejected fragments. This is the reason why the total ejected mass at the same P_SB for the unsupported shock is always larger than that for the supported shock, which also explains the distinct threshold of P_SB for ejecta production.

Compared to the MD simulations which accurately acquire the amount of the ejecta, the experiment captures this quantity directly from the areal density distribution, which integrates the volume density distribution beginning from the jet tip. This is an accumulated quantity representing the ejecta mass along the ejected direction. Figure 5 displays the cumulative areal density distribution as a function of the ejected velocity for both shock waves, correlating with the volume and velocity distributions of Fig. 2. These two plots reveal the smooth increase with the decreasing velocity, followed by a steep rise. The location denoted by dotted lines is experimentally thought of as the free surface which is identified as a referenced site in the ejecta mass measurements.^[2,10] But it is not the case for atomistic simulations performed here, as was also found in Ref. [21]. Based on the snapshot in Figs. 3(a) and 3(d), the free surface in Fig. 5 approximates to be V = 1.583 km/s for the supported shock and V = 0.885 km/s for the unsupported shock, both of which are beyond the jet bottom. At the free surface, the corresponding areal densities are 0.001278 mg/cm² and 0.002071 mg/cm², respectively, also indicating a larger number of the total ejected mass for unsupported shocks. The amount of areal density profile cannot be compared with the experiment [2,10] since the length scale here is nm while it is mm for the latter. Additionally, we should note that the jets partially break up into the ejecta and the rest near the jet bottom are reabsorbed back in the bulk.

Fig. 5.

	Figure Option ViewDownloadNew Window
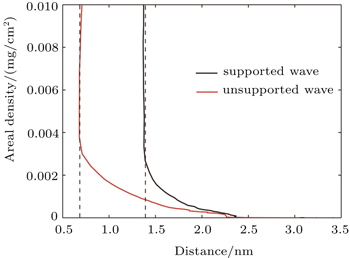	Fig. 5. The areal density distributions versus the ejected velocity are presented. The dashed line marks the bubble velocity for the jets.

It could be seen from the above results that the whole analysis on the ejected process for unsupported and supported shocks is reasonable; however, the total ejected mass changed with P_SB fully differ from the experiments of Sn sample.^[5,6] The underlying origin is due to the fact that the shocked sample between experiments and simulations undergoes the distinct loading histories. For the former, the shockwave decays very slowly and ejecta production is an instantaneous event, meaning that the ejecta formation time is a lot shorter compared to the shock travelling time within the bulk both for supported or unsupported shocks. Therefore, ejecta production mainly relies on the material state imposed by the first shock loading. For the latter, the shockwave loading time is short and ejecta production is a time-dependent process where the ejected time is comparable to the shock loading one. In this case, ejecta formation will be quickly affected by the following release wave from the back of the sample. This indicates that ejecta production in the MD simulation on such a small scale is associated with the material state and shockwave propagating process.

In conclusion, we have investigated the ejecta production from shocked Pb surface imposed by supported and unsupported shockwave loadings via molecular dynamics simulations. For the sake of convenient comparisons, shock-breakout pressure P_SB at the groove bottom is kept uniform for both shocks. The three phase states of solid, local melting and melt-on-shock for Pb metal are taken into account throughout the whole simulation. The simulated results show that total ejected mass for supported shocks is the same trend of increasing with P_SB as that under unsupported shocks and the former is always less than the latter at the same P_SB. The reason stems from a larger velocity difference between the jet tip and its bottom for unsupported shocks, which gives rise to the more serious damage and therefore more ejected fragments, as also observed in the spallation experiment.^[12,13] The origin is that for unsupported shocks the release wave from the backside of the sample immediately reaches the jet bottom, rapidly decreasing its velocity. Additionally, we made an explicit explanation of the difference between the simulated results and the experiments, which arises from the far larger ratio of sample thickness to groove depth. This needs to be considered in the future MD studies related to the ejecta process in contrast to the experimental case. Of course, our simulations performed here provide a clear picture and physical understanding for ejecta formation under these two loading profiles, which contributes to the development of an eject source model. It is suggested that the simulated results herein could be experimentally validated by a laser driven shock^[9] where the loading profile history is much closer to that via atomistic simulations.