† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11435011 and 11575034).
In this paper, a six-cylinder-port hohlraum is proposed to provide high symmetry flux on capsule. It is designed to ignite a capsule with 1.2-mm radius in indirect-drive inertial confinement fusion (ICF). Flux symmetry and laser energy are calculated by using three-dimensional view factor method and laser energy balance in hohlraum. Plasma conditions are analyzed based on the two-dimensional radiation-hydrodynamic simulations. There is no Ylm (l ⩽ 4) asymmetry in the six-cylinder-port hohlraum when the influences of laser entrance holes (LEHs) and laser spots cancel each other out with suitable target parameters. A radiation drive with 300 eV and good flux symmetry can be achieved by using a laser energy of 2.3 MJ and peak power of 500 TW. According to the simulations, the electron temperature and the electron density on the wall of laser cone are high and low, respectively, which are similar to those of outer cones in the hohlraums on National Ignition Facility (NIF). And the laser intensity is also as low as those of NIF outer cones. So the backscattering due to laser plasma interaction (LPI) is considered to be negligible. The six-cyliner-port hohlraum could be superior to the traditional cylindrical hohlraum and the octahedral hohlraum in both higher symmetry and lower backscattering without supplementary technology at an acceptable laser energy level. It is undoubted that the hohlraum will add to the diversity of ICF approaches.
The primary route to ignition and high gain in inertial confinement fusion (ICF) involves the use of hohlraums.[1] A hohlraum consists a high Z case with laser entrance holes (LEHs). The laser beams are efficiently converted into x rays at the beam spots on the hohlraum wall. The study and design of a hohlraum target are essentially important in inertial fusion because it seriously influences the capsule symmetry and the hohlraum energetics, which are the most important issues of inertial fusion.[1–3] Typical capsule convergence ratios range from 25 to 45, so that drive asymmetry can be no more than 1%,[1] a demanding specification for hohlraum design. The flux symmetry is strongly dependent on hohlraum geometry and laser beam arrangement. Up to now, various designs with different hohlraum geometries and beam arrangements have been proposed and investigated, such as cylindrical hohlraums[1,3] and spherical hohlraums with 4 LEHs[4,5] or 6 LEHs.[6–8] The cylindrical hohlraums are used most often in inertial fusion studies and are chosen as the ignition hohlraums on the US National Ignition Facility (NIF).[3] In cylindrical hohlraums, the Legendre polynomial modes P2 and P4 of the flux on capsule are the main asymmetry modes required to be controlled. The P2 asymmetry is controlled by using two rings per side in the hohlraum and by adjusting the power ratio between the two rings, the approach that is called beam phasing technology, on NIF.[9] However, the laser beams injected at inner cones encounter complicated laser plasma interaction (LPI) issues,[1] which reflects laser energy out of hohlraum directly and reduces the effect of the beam phasing technology. A crossed-beam energy transfer (CBET) [10] technique is used to maintain the required symmetry. It makes asymmetry control on NIF more complicated. The recent work[11] on NIF showed that the fusion fuel gains exceed unity by using a high-foot implosion method to reduce instability in the implosion., and the hot spot at band-time is still far from a sphere due to the neutron image. The analysis showed that the P2 symmetry of capsule is as high as −34%. This result shows that the capsule asymmetry is a still serious issue, which must be solved in future.
The spherical hohlraum with 4 LEHs[4,5] has no Y2m spherical harmonic asymmetry, but there exits Y3m asymmetry and it cannot be eliminated by adjusting the target parameters. In the spherical hohlraum[6–8] with 6 LEHs of octahedral symmetry (octahedral hohlraums), the three-dimensional (3D) laser arrangement shows that some laser beams are likely to be blocked by the high-Z plasmas created by other laser spots, which are just above these beams, destroying the symmetry control scheme. And some laser spots are very close to their neighbor LEHs in those hohlraums. Considering the nominal beam pointing errors, these laser beams are likely to transfer outside hohlraum directly. The high laser intensity of the octahedral hohlraum, due to the small laser spot, can result in high LPI risk, since LPI linear gains is proportional to the laser intensity.[1] And the laser beams are likely to be absorbed by the plasma at LEH due to the very small LEH radius. Besides, when the LEHs are not placed at the specific hohlraum-to-capsule radius ratio of 5.14,[6] there is a residual Y4m asymmetry and it is difficult to eliminate this asymmetry by adjusting target parameters.
In this paper, we investigate a hohlraum with six cylinder ports from theoretical side, addressing the most important issues of the flux symmetry, laser energy, and LPI.
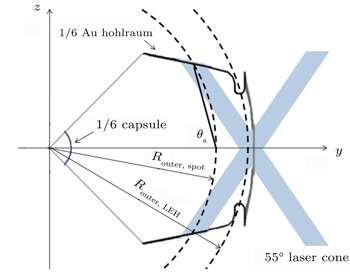
We consider a six-cylinder-port hohlraum with 192 laser beams for a capsule of 1.2-mm radius which is designed for a 300-eV radiation drive. The details of capsule are not discussed here.
Shown in Fig.
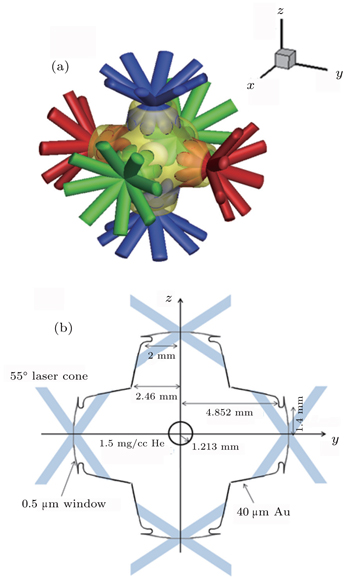 | Fig. 1. (a) Scenography of the hohlraum with six cyliner ports, 48 laser quads and centrally located fusion capsule. (b) Hohlraum specifications. |
As described in Ref. [12], there is an optimal configuration of NL LEHs on an outer sphere with radius Router, in which the total quantity of the NL LEHs 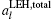
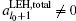
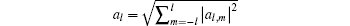
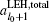
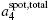
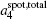
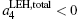
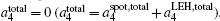
To verify the above theoretical prediction, we further use a 3D view factor code, based on Ref. [13], to calculate the radiation flux on the capsule. The asymmetry of flux on capsule can be decomposed into the spherical harmonics defined in quantum mechanics and blm is defined as harmonic decomposition. We further define Clm = blm/b00 to describe the quantity of the Ylm asymmetry. Shown in Fig.
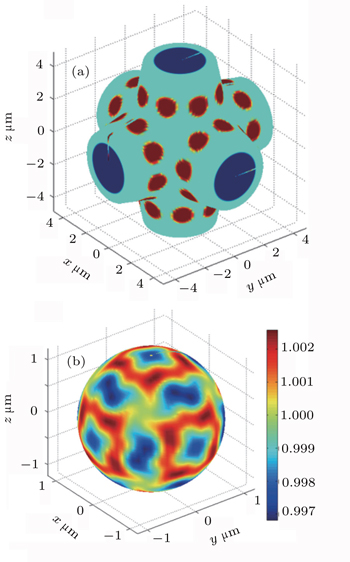 | Fig. 4. (a) Spot pattern on the wall of the six-cylinder-port hohlraum. (b) The relative flux 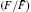  |
We use the energy balance[1] to relate the internal hohlraum radiation temperature to the input laser energy by balancing the absorbed laser energy with the x-ray energy radiated into the wall, EW, absorbed by the capsule, EC, and the energy that escapes through the LEH, ELEH, i.e.,
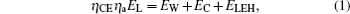
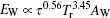
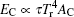

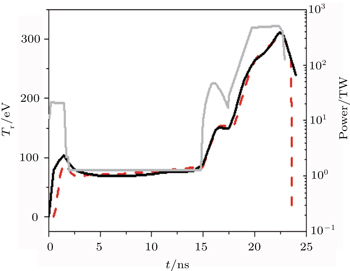
To study the plasma conditions of the cylinder ports by simulations, we consider one cylinder port with 1/6 laser energy on one cone in cylindrical symmetry, because we do not have a 3D hydrodynamics code for the six-cylinder-port hohlraum. The 1/6 capsule is inside the cylinder port. This simulation scheme is reasonable since the six cylinder ports are relatively independent of each other. It is noticeable that the sum of six single cylinder ports is not equivalent to the hohlraum with six cylinder ports, but their differences are too small to influence the plasma conditions and the energy balance very much. We use a 2D non-equilibrium radiation hydrodynamics code LARED-Integration.[16] Capsule needs a shaped radiation temperature to launch sequential shocks.[1] In our design, laser power is tuned to meet the driven temperature requirement of the capsule with 1.2-mm radius. Shown in Fig.
Maps of the spatial distributions of the electron density, the electron temperature, the x-ray emission, and the laser absorption at peak power are shown in Fig.
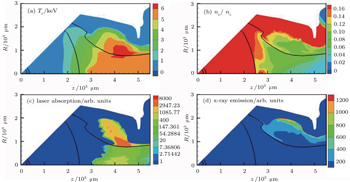 | Fig. 5. Maps of plasma at peak power: (a)Te in keV. (b) ne/nc. (c) Laser asorption.(d) x-ray emission. |
Without filling the gas, for laser pulse duration as long as those required for ignition, the Au blowoff driven by laser and radiation has time to fill the hohlraum, and the laser beam will not propagate to the initial impacting point since it is absorbed by the Au plasma filled in the hohlraum. This changes the x-ray emission position and destroys the symmetry control scheme. In our design, He gas at 1.5-mg/cc initial density holds back the Au blowoff and ensures that the path of laser cone is clear (Fig.
In this work, we propose a new ignition hohlraum with six cylinder ports for the capsule with 1.2-mm radius. We use the 3D view factor calculations, the energy balance analysis, and the 2D hydrodynamic simulations to study the hohlraum. Our theoretical study shows that the six-cylinder-port hohlraum has very high flux symmetry on capsule. Specially, the Y4m asymmetry, which exists in the octahedral hohlraum, can be adjusted to zero by cancelling the influences of laser spots and LEHs each other out, even though the LEHs are not on a sphere with golden radius ratio. About 2.3-MJ laser energy is required to provide the radiation driven of capsule. The simulations show that the plasma conditions in the hohlraum should simulate little SBS and the x-ray emission positions are still very close to the initial ones. Obviously, in addition to the residual Y4m problem, the other problems about laser transferring and LPI, mentioned before in the octahedral hohlraums, are solved or eased in the six-cylinder-port hohlraum. Next, we plan to study more in depth the time-varing Y4m asymmetry, the asymmetry of M-band flux and the laser beam entering problem because there is much room for optimization in the target design. Of course, in future, 3D simulations are necessary to classify the details of asymmetry, plasma, and efficiency in hohlraums. And aboundant experiments are worthy to be done with six-cylinder-port hohlraums on exiting facilities, since we have little experience of laser arrangement, target fabrication, and diagnostics.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 |