† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2012CB215003), the National Natural Science Foundation of China (Grant No. 91334204), the Fund from the Chinese Academy of Sciences (Grant No. XDA07080100), and China Postdoctoral Science Foundation (Grant No. 2014M561071).
The free path of a vibro-fluidized two-dimensional (2D) inelastic granular gas confined in a rectangular box is investigated by 2D event-driven molecular simulation. By tracking particles in the simulation, we analyze the local free path. The probability distribution of the free path shows a high tail deviating from the exponential prediction. The anisotropy of the free path is found when we separate the free path to x and y components. The probability distribution of y component is exponential, while x component has a high tail. The probability distribution of angle between the relative velocity and the unit vector joined two particle centers deviates from the distribution of two random vectors, indicating the existence of the dynamic heterogeneities in our system. We explain these results by resorting to the kinetic theory with two-peak velocity distribution. The kinetic theory agrees well with the simulation result.
Granular gases,[1,2] known as rapid granular flows, refer to the fact that macroscopic grains interact via instantaneous inelastic collisions. The granular gas is widespread not only in nature, such as interstellar dust, planetary rings, and avalanches, but also in the industry where the granular media are fluidized by shear, vibration or gravity. Given the presence of inelastic collision, it is different from the molecular gas by nature, featuring non-Maxwell velocity distribution, inhomogeneous density distribution (clustering and patterns), and lack of energy equipartition.[3,4] In particular, the velocity distribution of granular gases shows exponential distribution as confirmed in experiments[5–7] and simulations.[8] Two peaks of local velocity distribution were further found in simulation[8–10] and also in micro-gravity experiments.[11,12] In greater detail, the local velocity distributions of the vibration direction show two peaks in the marginal layer, melting into one peak in the box center, as demonstrated by the relevant skewness. All these suggest a granular gas may not reach fast local equilibrium. In order to study such non-equilibrium systems, we need to start from certain basic issues. The collision statistics, especially free path length or free flight time, which is useful in estimation of transport coefficient and the energy loss for granular gases, is supposed to be one of them.
The mean free path[13,14] is normally applied to characterize free path lengths. It is defined as the average distance that a molecule travels between successive collisions. It is a critical criterion that determines whether the granular dynamics can be described by the hydrodynamics or not[13,15] for granular gases. Besides, it can be used to calculate the transport property for granular media, such as viscosity.[8,14] The classical mean free path of molecular gases could be derived strictly from the Maxwell velocity distribution. Grossman et al.[16] gave mean free path expressions for granular gases in the low and high density limits in nearly elastic conditions. The low density expression is the same as the mean free path of molecular gases, while the high density one is deduced based on the close-packing density. In the above derivation, an important assumption is the molecular chaos (Stosszahlansatz), which supposes the velocity between two colliding particles is uncorrelated. Further, Brey et al.[8] used the local mean free path replacing the coordinate to obtain the spatial profiles of temperature for a granular gas fluidized by a vibrating wall and a reflecting one, then built a relationship between the velocity of the wall and the hydrodynamic profiles.
However, the free path in dissipated granular gases is different from that in elastic gases,[17–19] since the assumption of molecular chaos is based on the local equilibrium. For example, Blair and Kudrolli[17] reported an experiment of collision statistics of vibro-fluidized granular particles on an inclined plane. The distribution of the free path lengths does not follow a simple exponential form on density which is derived by the basic kinetic theory. Visco et al.[18] studied the probability distribution of the free flight time and the number of collisions in a hard sphere gas at equilibrium with three simulation methods, the Molecular Dynamics, Direct Simulation Monto Carlo, and Monte Carlo family. The results showed that the number of collision deviates from Poissonian statistics, whereas the probabilistic ballistic annihilation model[19] was found to be able to well explain the simulation results. Tan and Goldhirsch[20–23] studied the mean free path in a uniform shear flow, elucidating that the dimensional shear rate is not small even for strong dissipation and the ‘true’ mean free path is larger than that in equilibrium state. It is worth noting that the non-equilibrium features of dissipative granular gases are not fully considered in these works. For example, the two-peak local velocity distribution, as discussed above, has not been taken into account in their analysis.
To introduce the non-equilibrium feature into the analysis of the mean free path, in this work, we first present the event-driven molecular simulation method, in which the two-peak local velocity distributions are emphasized. Then the spacial profiles and the probability distribution of free path lengths, the probability of collision angles and the probability distribution of the components of free path lengths are presented. Based on two-peak velocity distribution model, the kinetic expression of the local free path is finally given. Comparison between our theory and simulation results are also discussed.
Granular gases consisting of N inelastic 2D particles (disks) with monodisperse diameter d = 1 and mass m = 1 are studied in a rectangular box. Figure 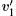
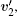
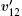
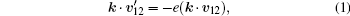
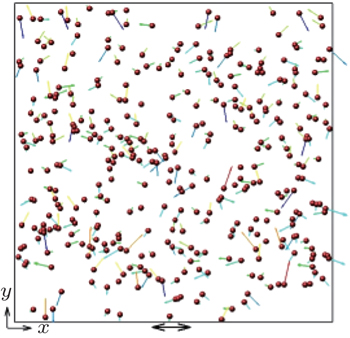 | Fig. 1. The schematic illustration of our simulations.[10] |
To drive the disks, we adopt the method used in Ref. [9], a sawtooth driving wall with vanishing amplitude A and diverging frequency ν in x direction. So each disk colliding with the wall has the post-collision velocity:
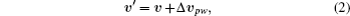
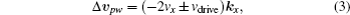
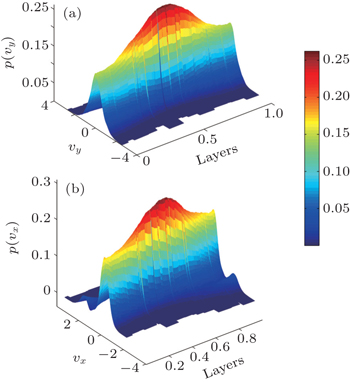
As in Ref. [11], we measure the local velocity distribution in each window which moves from the left side to the right side of the box. The three-dimensional plot of the local velocity distributions p(vx) and p(vy) are illustrated for an inelastic case with N = 1000, e = 0.9 in Fig.
For a molecule moving in an irregular, zigzag path, the mean free path, λ, is expressed in terms of the number density and diameter. For granular gases, two situations[16] are usually included for two-dimensional nearly elastic hard disk gases: in the low density limit, λ is given by
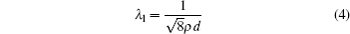
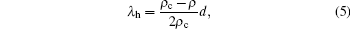
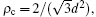
Both equations (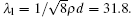
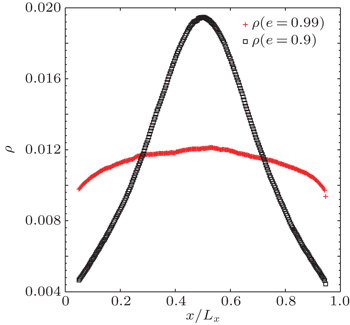 | Fig. 3. The spatial profiles of number density ρ with different restitution coefficient (e = 0.99 and e = 0.9), Lx = Ly = 300, N = 1000, Vdriven = 5. |
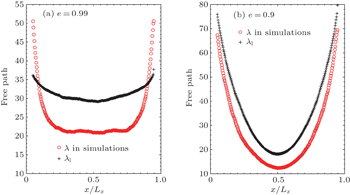 | Fig. 4. The spatial profiles of local free path λ, for (a) e = 0.99 and (b) e = 0.9. Other parameters are Lx = Ly = 300, N = 1000, Vdriven = 5. |
According to the kinetic theory, the distribution of free paths for nearly elastic particle is given by
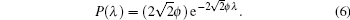
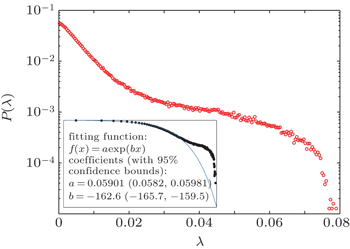 | Fig. 5. The probability distribution of free path lengths P(λ), where e = 0.9, Lx = 600, Ly = 300, N = 1000, Vdriven = 5. |
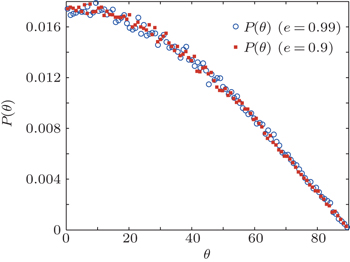
Further, we analyze the probability distribution of the angle between the relative velocity,
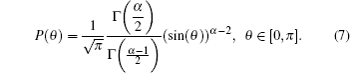
Considering the anisotropy due to boundary heating, we further investigate the anisotropic distribution of free path lengths and compare the x and y components of free path as shown in Fig. 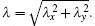
As presented in Section 2, the non-Maxwellian distribution can be described with a two-peak velocity distribution as shown in Fig.
We suppose the velocity distribution function is bimodal, which can be written as:
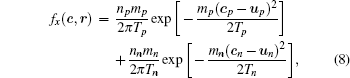
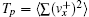
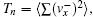
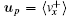
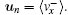

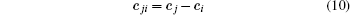
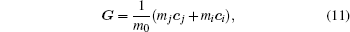
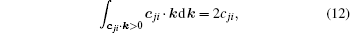
When
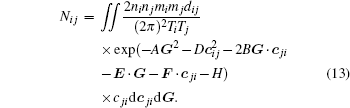
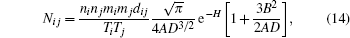

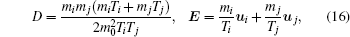
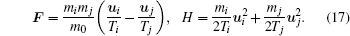
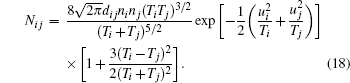
Then we can calculate the local free path based on Eq. (
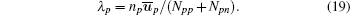

Figure
 | Fig. 8. Parametric plots of Eq. ( |
Although equations (
In all, our results evidence another mesoscopic nature of the granular gas. As mentioned in the shear granular system,[20] a mesoscopic system is different from the macroscopic one, particularly in average properties, so is the mean free path. The mean free path is obscure in such systems. The effect of boundaries is of much more importance in a granular system than in an elastic one. The asymmetric local velocity distribution implies the local mean free paths of positive and negative are different. Our results support this original hypothesis.
In this study, we focus on the local free path of vibrated granular gases through event-driven molecular dynamic simulation. The results demonstrate the local free path of granular gases is very different from the classical prediction. The probability distribution of the free path does not follow an exponential distribution expected by the classical elastic kinetic theory. Instead, anisotropy of the free path is found where the non-vibrating direction component of the probability of free path lengths is still exponential, while the vibrating direction component has a high tail. The probability distribution of angle between the relative velocity and the unit vector directed two particle centers disagrees with the distribution of two random vectors. Using the two-peak velocity distribution, we provide an expression of the free path based on the kinetic theory, which shows the local free path is related not only to the number density, but also to the granular temperature. The two-peak model results agree well with simulation, demonstrating the effect of non-equilibrium distribution. Future work will be directed to the experimental measurement of the free path and the mechanism underlying the two-peak distribution.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 |