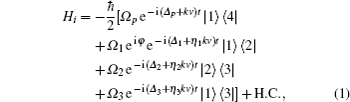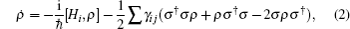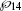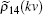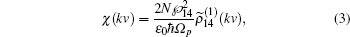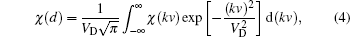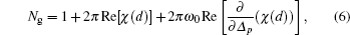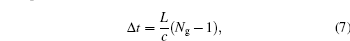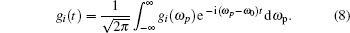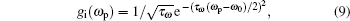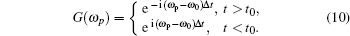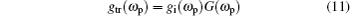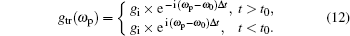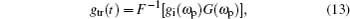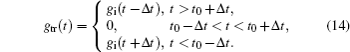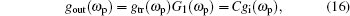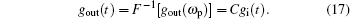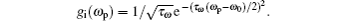Department of Physics, University of Malakand, Chakdara Dir(L), Pakistan
† Corresponding author. E-mail: a jabar80@yahoo.com or aminoptics@gmail.com
Project supported by the Higher Education Commission (HEC) of Pakistan.
1. IntroductionThe process of manipulating the speed of light in such a way that a time gap is created in it is called temporal or event cloaking. An event occurring in the time gap is cloaked from the detectors. The time gap is then closed so that a specific observer could receive the information of light in its original form. The ability to hide events opens a number of new exciting possibilities in quantum optics.[1] An interesting feature of the temporal cloak is that it works simply by speeding up and slowing light down, no diversion or realignment of light is required.[2]
Event cloaking has been extensively studied theoreti-cally[3,4] as well as experimentally[5] during the last few years. Based on the transformation optics formalism,[6,7] initially established for the invisibility cloaking,[8,9] the event cloaking was first introduced in a theoretical research work[10] in 2011, whereas, hiding of an isolated time event was experimentally[11] reported, for the first time, in 2012. A time window up to tens of picoseconds was created in the probe light beam. However, the stability of the cloak was limited due to the short time window to hide any practical event. A group of researchers lead by Andrew M Weiner[12,13] demonstrated temporal cloak by considering the temporal Talbot effect and the temporal analogue of Lau effect for their experiments. In their first experiment a cloaking time window up to 46% of the entire time axis was achieved. A multi-wavelength cloak, in which optical data was found hidden at one of the input frequencies but was transmitted along another wavelength, was reported in their second experiment. Bony et al.[14] demonstrated temporal cloak on the basis of self-organization of polarization states of light in optical fibres through a reversible nonlinear process. Their cloak operated over an arbitrarily long temporal window and succeeded to hide 100% of a 10-Gb/s transmitted signal. Meanwhile, a theoretical model was proposed to create and close a temporal gap with different transfer functions by using the Fourier analysis method.[15] A temporal cloaking scheme based on tunable optical delay and advance, where an optical data stream was used as the probe beam, was also demonstrated.[16] The fact that atomic medium is playing a vital role in several interesting optical phenomena, such as Refs. [17]–[21], is well known to every researcher of the field. The temporal cloaking operation, based on quantum destructive interference, was reported for the first time in atomic medium, where a temporal window was created in a long optical pulse propagating through a three level warm atomic system.[22]
Being inspired by the achievements mentioned above, in the present article, we propose a different theoretical approach to create a temporal window in a probe laser pulse, based on spectral hole burning in a Doppler broadened four-level sodium atomic system, as slow and fast light may be generated in the hole burning phenomenon.[23,24] We consider the Fourier analysis method[15] for our scheme because the spectral hole burning mechanism has the capability to write and read data, not only in the spatial dimensions but also in the dimension of frequency, which is related to the time dimensions via the Fourier transform.[25] A temporal window in microseconds is created in the slow light of the hole burnt region as well as between this slow and the fast light near a hole region. From this scheme one may envision to create multiple temporal windows in the light pulse propagating through an atomic medium.
2. Model and its dynamicsOur proposed atomic model for temporal cloaking is schematically shown in Fig. 1. This is a closed four-level hyperfine structure of sodium D1 line having the ground states |1〉 and |2〉 while excited states |3〉 and |4〉. The ground level |1〉 is coupled with the excited levels |4〉 and level |3〉 by a probe and a control field of Rabi frequencies Ωp and Ω3 respectively. The corresponding detunings are denoted as Δp and Δ3 respectively. Level |1〉 is coupled with level |2〉 by a control field of Rabi frequency Ω1 having detuning Δ1 while a coupling field of Rabi frequency Ω2 is applied between levels |2〉 and |3〉 having detuning Δ2. The decay rates from upper to lower states are expressed as γ41, γ21, γ32, and γ43.
In order to analyze the optical response function of the proposed system, the following Doppler effected interaction picture Hamiltonian is proceeded in the dipole and rotating wave approximations:
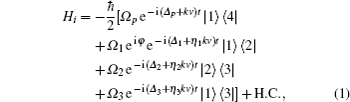
where
k is the wave vector,
v is the atomic speed,
η1,2,3 represent the propagation directions, and
φ is the phase of the field. The general form of the density matrix equation is written as follows:
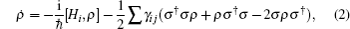
where,
σ† and
σ are raising and lowering operators respectively while
γi j represent decay rates. The important coupling rates equations for the system are obtained by using the general Eq. (
2) and are presented in the Appendix A. To analyze the probe field propagation in the system, we evaluate the complex susceptibility of the system as its real and imaginary parts are associated with the absorption and dispersion spectrum of the probe field respectively. The complex susceptibility of an atomic medium is related to the electric polarization of the medium by the equation
P =
ɛ0 χE while the probe coherence and polarization in the system are related by the relation

. Here,
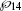
is the dipole matrix element and
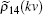
is written in the Appendix A. By comparing the above two polarizations, the complex susceptibility for the proposed atomic system is obtained. The first order velocity-dependent complex susceptibility for the system is written as
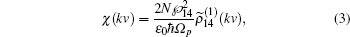
where
N is for the atomic density. The Doppler susceptibilities is the average of
χ(
kv) over the Maxwellian distribution and is described as
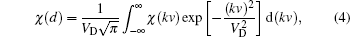
where
VD is the Doppler width and depends upon the absolute temperature. Its value is written as

where
ωp is the frequency of probe field,
KB is the Boltzmann constant,
T is the absolute temperature,
M is the molecular mass, and
c is the speed of light in vacuum. The group index
Ng of the Doppler broadened system is written as
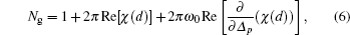
where
ω0 is the central frequency of the probe field. The difference in time of a light pulse when it propagates in the medium of length (
L) and if the same length is traversed in free space can be written as:
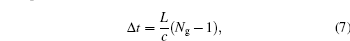
L is supposed to be 10 cm. Δ
t is positive for
Ng > 1, means that the propagation time delays in the medium. Δ
t is negative for
Ng < 1 which means that the propagation time advances in the medium. A wave packet in time domain may be described as
[15]
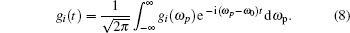
For our proposed system, this wave packet in frequency domain is considered of the Gaussian form as:
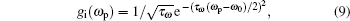
where
ωp−
ω0 =
Δp and
τω is the input pulse width in time domain and is supposed to be 1.5 μs.
gi(
ωp) and
gi(
t) are the Fourier and inverse Fourier transforms of one another respectively. The Gaussian pulse has the minimum uncertainty because the Fourier transform of Gaussian pulse is again Gaussian. Delay or advancement in time of the wave packet is caused because of its phase shift in frequency domain in accordance with the phase shift theorem.
[26] For the incident wave packet
gi(
t), the delay or advancement creates a phase shift e
−iωpΔt around the central time
t0. To create a time gap in the pulse spectrum, transfer function
G(
ωp) of the dispersive medium is described as
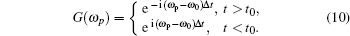
The transmission frequency spectrum gtr(ωp) of the incident event gi(ωp) is then equal to the product
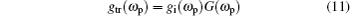
or
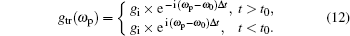
This transmission function is obtained in time domain by taking its inverse Fourier transform as
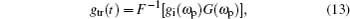
where
gtr(
t) is a piece-wise continuous function, so by applying shift theorem we get the transmission frequency spectrum in the following ranges
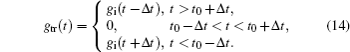
The interval
t0 − Δ
t <
t <
t0 + Δ
t, where the transmission function is zero means that a temporal gap of width 2Δ
t is created in the transmission frequency spectrum. If an external event
gint(
t) interacts with
gtr(
t) in the gap then
gint(
t)
gtr(
t) = 0. The transmitted wave packet experiences no effect of the interacting event that occurs inside the temporal gap. The information of the wave packet is hidden in the gap and it will transmit without being detected until the gap is closed. For the specific observer to receive the original information of the incident wave packet, the temporal gap is closed. In this case, the transfer function is described as

which is just the complex conjugate of the initial transfer function. The output transmission frequency spectrum of the
gi(
ωp) is then written as
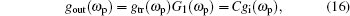
where
C is constant. The output signal in time domain is obtained by taking the inverse Fourier transform of
gout(
ωp) as
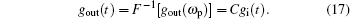
For the output signal to be distortion-less,
C = 1.
3. Results and discussionsThe propagation of the light pulse through a four-level sodium atomic system is investigated in the presence of Doppler broadening effect. For simplicity atomic units (shortened to a.u.) are used throughout this paper. A scaling parameter Γ is supposed to be 1 GHz and all other parameters are scaled to this Γ.
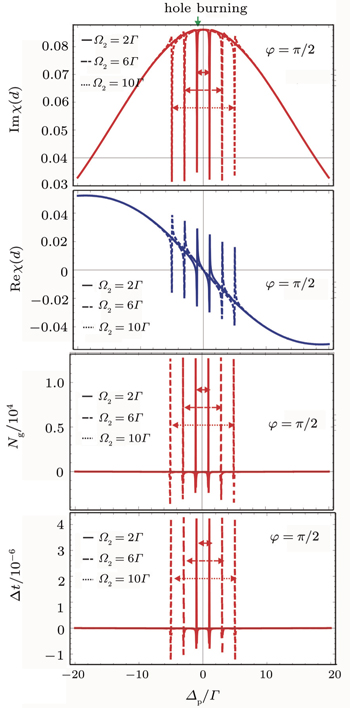
In Fig. 2, for the mentioned spectroscopic parameters, two spectral holes are observed on either side of the resonance line in absorption spectrum of the probe field. These holes shift away from the resonance line with increase in the Rabi frequency Ω2 of the control field. The slope of dispersion is normal in the hole regions while it becomes steeply anomalous in the adjacent regions, as shown in the real part of the susceptibility. The normal dispersion is observed to shift away from the resonance, while the anomalous dispersion is observed to increase with increase in Ω2. Large positive and small negative group indexes are observed respectively in the hole and near the hole regions. The negative group index increases as the holes shift away from the resonance. The corresponding delay/advance time is shown in the lower plot of Fig. 2. The advance time increases with increase in Ω2.
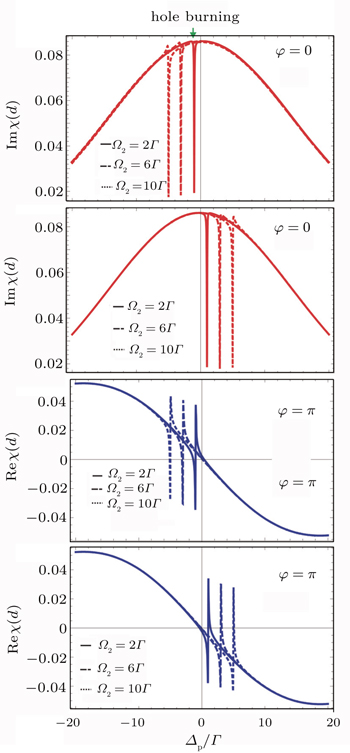
Absorption and dispersion at the two phases φ = π, 0 are presented in Fig. 3. A single hole is observed at the opposite side of the resonance line for each phase. The hole shifts away from the resonance line when Rabi frequency Ω2 is increased while the Doppler width is kept constant. In the hole region the dispersion is normal and shifts away from the resonance while it becomes steeply anomalous near the hole region. The anomalous dispersion is observed to increase with increase in Ω2. A similar behavior like Fig. 2 can also be observed for the group index and delay/advance time.
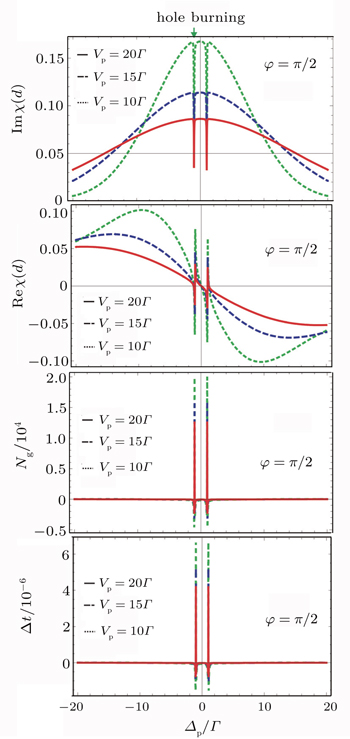
In Fig. 4, propagation of the probe field is investigated with increase in the Doppler width while Rabi frequencies of the control fields are kept constant. Depths of the spectral holes are observed to decrease as the Doppler width is increased. The slope of dispersion is normal in a hole region but it becomes steeply anomalous near a hole region. Normal and anomalous dispersions are observed to decrease with increase in the Doppler width. The corresponding group index and delay/advance time are also observed to decrease. At the Doppler width of 10Γ the group index is about 2×104 in the hole region while it is −4500 near the hole region. Step-wise decrease of the positive as well as the negative group index is observed as the Doppler width is increased to 15Γ and then to 20Γ respectively. A delay time of 6.7 μs is observed at VD = 10Γ which decreases to 5.3 μs and then to 4.2 μs when VD is increased to 15Γ and then to 20Γ respectively. An advance time of 1.4 μs is initially observed which decreases to 0.8 μs and then to 0.6 μs with increase of the Doppler width from 10Γ to 15Γ and then to 20Γ respectively.
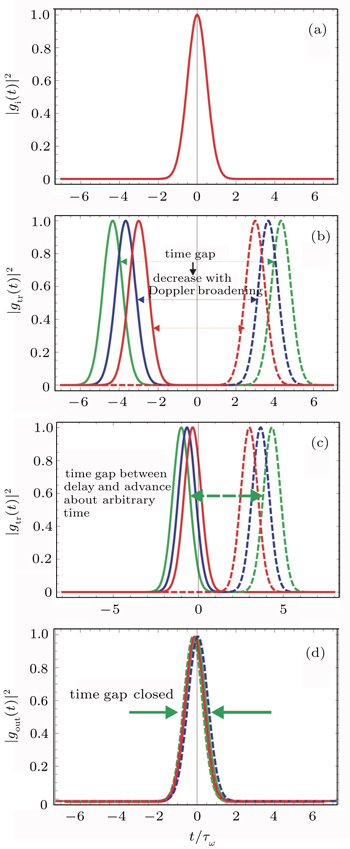
In Fig. 5, panel (a) shows the normalized input pulse, whereas panel (b) shows the time gap created in the slow light of the hole burnt region. The time gap is opened due to phase shifts of the probe pulse about the central time t0 and is symmetric about t0. The width of the time gap is equal to 2Δt. A time gap of 13.4 μs is observed at the Doppler width, VD = 10Γ. This time gap decreases to 10.6 μs and then to 8.4 μs when the Doppler width is step-wise increased to 15Γ and then to 20Γ respectively. The information of the probe will be transmitted undetected if the subluminality is enhanced and the Doppler width up to 10Γ significantly contributes to enhancement in subluminality in this medium. Further increase of the Doppler width will lead to decrease of the subluminality. Plot (c) shows the time gap created between the slow light in the hole region and the fast light near the hole region about an arbitrary time. The time gap is not symmetric as large delay and small advance is observed in the two regions. A time gap of 8.1 μs is observed at VD = 10Γ. This time gap decreases to 6.1 μs and then to 4.8 μs as the Doppler width is increased to 15Γ and then to 20Γ. Here the probe pulse splits into two parts, a slow part in the burnt hole region but a fast part near the hole region and therefore a temporal gap is created. Once the time gap is created the information securely transmits until the gap is closed. For the specific observer to receive the information of the pulse in its original initial form, the gap is closed by the reverse process. The closed time gap is shown in plot (d) of Fig. 5. Here we have discussed only the influence of the doppler width on the time gap, however, the time gap can also be tuned and modified with other parameters like Ω1,2,3, specifically, with Ω2 and φ, as we have also analyzed the probe field propagation with these parameters.
Our proposed temporal cloaking scheme is based on spectral hole burning phenomenon caused by the saturation excitation effect in this atomic system. This scheme is completely different from the one[22] which is based on atomic coherence effect in a three level atomic system. The fundamental advantage of our scheme is that hole burning has the capability to write and read data not only in the spatial dimensions but also in the dimension of time. Addressing of data in the frequency dimensions makes use of frequency-specific photo-induced transformation with Doppler broadening in the system.[25] We consider a Gaussian shaped input pulse as
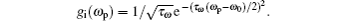
The transmitted pulse amplitude is normalized to the input pulse width. The advantage of the Gaussian pulse in this atomic medium is that its spectral width is well contained within the region of the burning-hole at resonance in the medium. That is why the transmitted pulse is either undistorted or it has negligible distortion while its transmission in the condition of hole burning is the same as that of saturated absorption spectroscopy. Apart from temporal cloaking, undistorted large delay or advancement of the light pulse may find applications in optical memories, optical buffers, data synchronization and in signal processing, as our proposed sodium D1 line system is an experimentally verified system. Further, the generation of slow light in the hole burning region and of fast light in the nearest neighbor region of a hole, leads to the creation of a temporal gap between the slow and the fast light. Our scheme may allow rapid switching between the slow and fast light like the one recently reported in Ref. [
24]. This may lead to the possibility of creating multiple temporal gaps where the data will be securely transmitted.
4. ConclusionIn this article, we have demonstrated for the first time, the possibility of creating a temporal gap based on the spectral hole burning phenomenon in a four-level Doppler broadened sodium atomic system. In this system ground state |1〉 and excited state |4〉 are coupled by a probe field. Three other coupling fields are applied in the system to control the dispersion properties of the system. The probe pulse is observed to delay in the hole burning region while it advances near a burnt hole region. The delay and advancement in the pulse creates a temporal time gap for hiding information. A time gap in microseconds is observed in the slow light as well as in the simultaneous slow and fast light. The width of the time gap varies with the inverse Doppler effect while the transmitted pulse is observed to be undistorted. The time gap may also be tuned and modified with the strengths of the coupling fields while keeping the Doppler width constant. Our scheme of temporal cloak may provide the base for creating multiple temporal gaps in atomic medium.