Cite this Article
Yan Xiang, Zhang Peng-Fei, Zhang Jing-Hui, Qiao Chun-Hong, Fan Cheng-Yu. Quantum polarization fluctuations of partially coherent dark hollow beams in non-Kolmogorov turbulence atmosphere. Chinese Physics B, 2016, 25(8): 084204  
Permissions
Quantum polarization fluctuations of partially coherent dark hollow beams in non-Kolmogorov turbulence atmosphere
Yan Xiang1, 2, Zhang Peng-Fei1, Zhang Jing-Hui1, Qiao Chun-Hong1, Fan Cheng-Yu1, †,
Key Laboratory of Atmospheric Composition and Optical Radiation, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China
University of Science and Technology of China, Hefei 230026, China

 

† Corresponding author. E-mail: cyfan@aiofm.ac.cn

Project supported by the Major Research Plan of the National Natural Science Foundation of China (Grant No. 61405205).

Abstract
Abstract

Non-classical polarization properties of dark hollow beams propagating through non-Kolmogorov turbulence are studied. The analytic equation for the polarization degree of the quantization partially coherent dark hollow beams is obtained. It is found that the polarization fluctuations of the quantization partially coherent dark hollow beams are dependent on the turbulence factors and beam parameters with the detection photon numbers. Furthermore, an investigation of the changes in the on-axis propagation point and off-axis propagation point shows that the polarization degree of the quantization partially coherent dark hollow beams presents oscillation for a short propagation distance and gradually returns to zero for a sufficiently long distance.

PACS: 42.50.–p;03.67.Mn;03.65.Ud
Keyword:polarization;turbulent atmosphere;partially coherent dark hollow beams;non-Kolmogorov turbulence
1. Introduction

Polarization is a key ingredient of a light beam which has a number of practical applications both in the quantum and classical realms.[1–10] In recent years, growing attention has been focused on the polarization fluctuations of quantum light propagating through a turbulent atmosphere since it plays an important role in free-space optical communications and remote sensing.[11–13] The polarization properties of a linearly polarized quantum beam in turbulent atmosphere have been reported.[14–17] But, few schemes studied the quantum polarization fluctuations of two-orthogonally-polarized-mode field propagation through the turbulent atmosphere.

Dark hollow beams (DHBs) are the beams with zero on-axis intensity which have important applications in laser optics, atomic optics, binary optics, optical trapping of particles and medical sciences.[18] DHBs can be generated by using various methods, such as geometrical optical method, mode conversion, optical holography, transverse-mode selection, hollow-fiber method, etc.[19–24] DHBs have many advantages over a Gaussian beam and flat-topped beam for overcoming the destructive effect of atmospheric turbulence from the aspect of scintillation,[25,26] hence, have important potential applications in free-space optical communications. Up to now, the propagation properties of the partially coherent DHB in turbulent atmosphere have been studied and the polarization degree of partially coherent DHB has also been reported.[27–29] However, the quantum polarization fluctuation of quantization partially coherent DHB has not been formulated yet. According to the two unsettled issues stated above, in this paper, by using quantum Stokes operators and non-Kolmogorov spectrum model of index-of-refraction fluctuation, we develop a theoretical model for the quantum polarization fluctuations of the two-orthogonally-polarized-mode quantization partially coherent DHB propagating in a turbulent atmosphere.

The rest of this paper is organized as follows. In Section 2 we summarize the necessary basic principles of the quantum Stokes operators and the polarization degree of the two-orthogonally-polarized-mode field. In Section 3 the quantum Stokes operators in a turbulent atmosphere are studied and the degree of polarization of quantization partially coherent DHB in a turbulent atmosphere is obtained. Numerical results and discussions are given in Section 4. Conclusions are presented in Section 5.

2. Quantum Stokes operators and the degree of the polarization for two-orthogonally-polarized-mode field

The polarization state of the two-orthogonally-polarized-mode field can be characterized by the Stokes operators:[30]

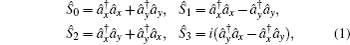
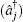
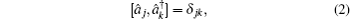
where âj is the photon annihilation (creation) operators in the model (q,j), respectively, with q being the momentum of a photon, and j its polarization.

where j,k = x,y.

We assume that two-orthogonally-polarized-mode field is initially in the Fock state, i.e.

where nj and |nj〉 are the eigenvalue and the eigenstate of the number operator, and |ξ〉 is the state of the total field containing two modes.

The degree of polarization for two orthogonally polarized modes of light when it propagates through a turbulent atmosphere can take the form

where denotes average over the ensemble of the source of the turbulent atmosphere.

For two orthogonally polarized modes of light, where âx ≠ 0 and ây ≠ 0, one can obtain

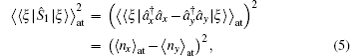
Then the degree of polarization can be expressed as

3. Quantum Stokes operators in a turbulent atmosphere

The propagating quantum field in the turbulent atmosphere can be expressed as

where τ is the transmittance of channel,j = x,y, ρ and ρ′ denote transverse coordinates of the photon at the z plane and source plane (z = 0) respectively, φ (ρ,ρ′,z) represents a random distortion which describes the effect of the atmospheric turbulence on the propagation of a spherical wave, k = 2π/λ is the wave vector of the light. At z = 0plane, the quantum field can be given by

where âj (q,ρ′) = âoj (q)u(ρ′) is the effective photon annihilation operator, u(ρ′) is the transverse beam amplitude function for the beam modes. By Eqs. (9) and (10), the propagating quantum field can be described as

Therefore, the effective photon annihilation operator can be expressed in the following form:

The effective photon creation operator can be written as follows:

We choose the quantum field to be a partially coherent DHB so that[31]

where and denote a binomial coefficient, N is the order of the partially coherent DHB, ωp = pω0, with ω0 being the beam waist size of the fundamental Gaussian mode, p is a scaling factor for controlling the dark size of the DHB satisfying 0 < p < 1, and σ0 is the transverse coherence width.

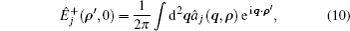
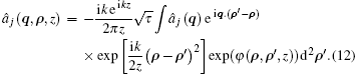
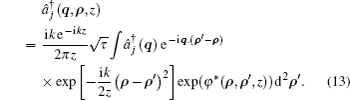
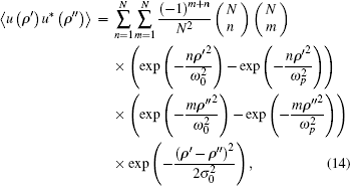
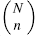
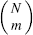
The ensemble average photon number of j polarization mode of quantum field when it propagates through a turbulent atmosphere can be obtained as

where nj = n0j τ is the detection photon number. Using the non-Kolmogorov power spectrum of atmospheric turbulence and taking into account the quadratic approximation for Rytov’s phase structure function, we have

where ρ0 is the spatial radius of a spherical wave propagation in turbulent atmosphere, and

α being the spectrum power of the refractive-index fluctuations (abbreviated as the refractive-index power). κ0 = 2π/L0, L0 being the outer scale of turbulence, κm = c(α)/l0, l0 being the inner scale of turbulence,

Γ(x) being the gamma function of the term. is a generalized refractive-index structure parameter.

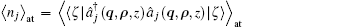
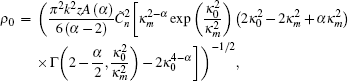
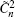
After tedious integral calculations, the photon number of quantization partially coherent DHB for two orthogonally polarized modes in atmospheric turbulence is obtained as

where

Substituting Eq. (17) into Eq. (8), we can obtain the formula for the polarization degree of quantization partially coherent DHB propagating through a turbulent atmosphere as

4. Numerical calculation and analysis

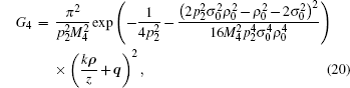
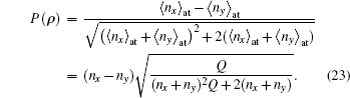
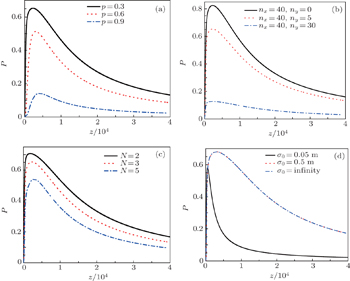
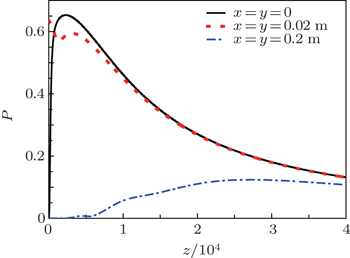
Based on the derived analytical results in the above section, we study the numerical results of the influence of turbulence on the polarization degree of quantization partially coherent DHB. The non-Kolmogorov spectrum parameters are set to be L0 = 1 m, l0 = 0.001 m, , and α = 3.8. The beam parameters and detection photon numbers in two orthogonally polarized modes are set to be p = 0.3, N = 3, σ0 = 0.05 m, w0 = 0.05 m, nx = 40, and ny = 5, and the other physical parameters of the system are λ = 1.55 μm and the photon moment q = 4.27 × 10−28.

Figures 1 and 2 show the changes in polarization degree of quantization partially coherent DHB propagating through non-Kolmogorov turbulence with propagation distance z for different spectrum parameters and different beam parameters with detection photon numbers in two orthogonally polarized modes. Figures 1(a)–1(d) show that for the on-axis propagation point the polarization degree of quantization partially coherent DHB first reaches its maximum value in the near field and finally approaches to zero. When the robustness of polarization is taken as the carrier in quantum information processing, the higher spectrum power-law exponent and inner scale of turbulence or smaller refractive index structure constants and outer scale of turbulence should be required.

Fig. 1. Degree of polarization along the z axis of quantization partially coherent DHB beams propagating through non-Kolmogorov turbulence: (a) for different spectrum power-law exponents, (b) for different refractive index structure constants, (c) for different outer scales of turbulence, (d) for different inner scales of turbulence.
Fig. 2. Degrees of polarization along the z axis of quantization partially coherent DHB beams propagating through non-Kolmogorov turbulence: (a) for the different values of parameter p, (b) for different detection photon numbers in two orthogonally polarized modes, (c) for different values of beam order (N), and (d) for the different values of coherent length (σ0.

Figures 2(a)–2(c) indicate that as the propagation distance increases, for on-axis propagation point the polarization degree of quantization partially coherent DHB has an oscillatory behavior at first and then it gradually decreases to zero. The quantum polarization fluctuation would be less for smaller parameter p and beam order or much difference between in detection photon numbers between two orthogonally polarized modes. In Fig. 2(d), it can be seen under the condition σ0 ≥ 0.5 m, the influence of the degree of polarization is slight.

Figure 3 shows the changes in the polarization degree of quantization DHB propagating through non-Kolmogorov turbulence with propagation distance z for different off-axis propagation points and on-axis propagation points. One can find no matter what the propagation point is, the polarization degree of quantization partially coherent DHB will return to zero after it has propagated over a sufficiently long distance.

Fig. 3. Degrees of polarization along the z axis of quantization partially coherent DHB beams propagating through non-Kolmogorov turbulence for different off-axis propagation points and on-axis propagation points.
5. Conclusions

In this work, we propose a theoretical model to describe the polarization degree of the two-orthogonally-polarized-mode quantization DHB propagating through non-Kolmogorov turbulence. The analytical expression for the polarization degree of the two-orthogonally-polarized-mode quantization partially coherent DHB is obtained. The polarization degree of the two-orthogonally-polarized mode quantization partially coherent DHB is investigated for the turbulence factors and beam parameters with the detection photon numbers. An investigation of the changes in the on-axis propagation point and off-axis propagation points shows that the polarization degree of quantization partially coherent DHB presents oscillation for a short propagation distance and gradually returns to zero for a sufficiently long distance. That is to say, the quantum optics will turn into the classical optics as the beam propagates. Furthermore, the quantum polarization fluctuation is slight for great difference in detection photon number between two orthogonally polarized modes: the higher the spectrum power-law exponent, the larger the inner scale of turbulence and coherent length, or the smaller the refractive index structure constants, outer scale of turbulence, central dark sizes p and beam order N are. Therefore, we should choose very different detection photon numbers in two orthogonally polarized modes, smaller central dark size p, smaller beam order N and weak turbulence, when the robustness of polarization is taken as the carrier in quantum information processing. The result can be employed in applications, such as free-space optical communications and remote sensing.

Reference
1Hodara H 1966 Proc. IEEE 54 368
2Collett EAlferness R 1972 J. Opt. Soc. Am. 62 529
3Anufriev A VZimin Yu AVolflpov A LMatveev I N 1983 J. Quantum Electron. 13 1627
4James DAniel F V 1994 J. Opt. Soc. Am. 11 1641
5Fried D LMevers G E 1965 J. Opt. Soc. Am. 55 740
6Hohn H 1969 Appl. Opt. 8 367
7Toyoshima MTakenaka HShoji YTakayama YKoyama YKunimori H 2009 Opt. Express 17 22333
8Chen JLi YWu GZeng H P 2007 Acta Phys. Sin. 56 9 (in Chinese)
9Dong C H2005Acta Phys. Sin.54687(in Chinese)
10Karimi ATavassoly M K 2016 Chin. Phys. 25 040303
11Mohamed SOlga KAristide DEmil W 2004 Waves in Random Media 14 513
12Ji XChen X 2009 Opt. Laser Technol. 41 165
13Kashani F DAlavinejad MGhafary B 2009 Opt. Commun. 282 4029
14Wang Y GZhang Y XWang J YJia J J 2011 Opt. Commun. 284 3221
15Wang Y GZhang Y XWang J YJia J J 2012 Opt. Laser Technol. 44 1446
16Zhang Y XWang Y GWang J YJia J J 2012 Optik 123 1511
17Zhang L CZhang Y XZhu Y 2013 Prog. Electromagn. Res. 140 471
18Yin JGao WZhu Y2003Progress in OpticsWolf EAmsterdamNorth Holland119204119–204
19Wang XLittman M G 1993 Opt. Lett. 18 767
20Lee H SStewart B WChoi KFenichel H 1994 Phys. Rev. 49 4922
21Yin JNoh HLee KKim KWang YJhe W 1997 Opt. Commun. 138 287
22Heckenberg N RMcDuff RSmith C PWhite A G 1992 Opt. Lett. 17 221
23Liu ZZhao HLiu JLin JAhmad M ALiu S 2007 Opt. Lett. 32 2076
24Liu ZDai JSun XLiu S 2008 Opt. Express 16 19926
25Cai YHe S 2006 Opt. Express 14 1353
26Chen YCai YEyyuboǧlu H TBaykal Y 2008 Appl. Phys. 90 87
27Yuan YCai YQu JEyyuboglu H TBaykal YKorotkova O 2009 Opt. Express 17 17345
28Wang HLi X 2010 Opt. Lasers Eng. 48 48
29Taherabadi GAlavynejad MKashani F DGhafary BYousefi M 2012 Opt. Commun. 285 2017
30Alodjants APArakelian S MChirkin A S 1998 Appl. Phys. 66 53
31Yuan Y SYangjian Cai Y JQu JEyyuboǧlu H TBaykal YKorotkova O 2009 Opt. Express 17 17344