† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61377054).
The circular dichroism (CD) signal of a two-dimensional (2D) chiral meta-surface is usually weak, where the difference between the transmitted (or reflected) right and left circular polarization is barely small. We present a general method to enhance the reflective CD spectrum, by adding a layer of reflective film behind the meta-surface. The light passes through the chiral meta-surface and propagates towards the reflector, where it is reflected back and further interacts with the chiral meta-surface. The light is reflected back and forth between these two layers, forming a Fabry–Perot type resonance, which interacts with the localized surface plasmonic resonance (LSPR) mode and greatly enhances the CD signal of the light wave leaving the meta-surface. We numerically calculate the CD enhancing effect of an L-shaped chiral meta-surface on a gold film in the visible range. Compared with the single layer meta-surface, the L-shaped chiral meta-surface has a CD maximum that is dramatically increased to 1. The analysis of reflection efficiency reveals that our design can be used to realize a reflective circular polarizer. Corresponding mode analysis shows that the huge CD originates from the hybrid mode comprised of FP mode and LSPR. Our results provide a general approach to enhancing the CD signal of a chiral meta-surface and can be used in areas like biosensing, circular polarizer, integrated photonics, etc.
Chirality is a fundamental and ubiquitous property of natural materials and biomolecules, which, in a two-dimensional (2D) case, refers to the phenomenon that a structure cannot be superimposed into its mirror image without turning the structure over. In the last decade, chiral plasmonics has aroused a considerable research interest for its importance in the fields like polarization control,[1–12] negative metamaterials,[13] biosensing,[14] repulsive Casimir force,[15] etc. Novel electromagnetic properties have been realized due to the large chiral response in these plasmonic applications, such as asymmetric transmission,[4] broadband circular polarization conversion,[12] attomolar limit of detection for DNA,[14] and nondispersive optical activity.[16] The strength of chirality can be measured with the circular dichroism (CD) spectrum, which is usually the difference in transmission efficiency between left (LCP) and right circular polarized (RCP) incident light. However, the chirality strengths of natural materials are very weak. The progress of research in plasmonic and nanofabrication technique allows us to realize artificial chiral materials that are so-called chiral meta-materials (CMMs),[1–17] whose chiral effects are much higher than those of natural materials. Previously proposed structures can be divided into two types, the first type of structure is the 2D structure, including dual-layer twisted-layers,[1,2] multilayer gammadions,[3] U-shaped split ring resonators,[4,5] nonchiral square arrays,[6,7] etc. The second type of structure is the three-dimensional (3D) structure, such as metal-doped platinum clusters,[8] helical metamaterial,[9–11] and complex colloids.[12] Among the above devices, the 3D chiral structure has larger CD response, however, is difficult to fabricate and hard to use in the frequency range from visible to ultraviolet band. On the contrary, the 2D structure can be realized in an easier way. Giant CD has been achieved by layers of 2D CMMs which can act as a circular polarizer.[6] However, the CD of single meta-surface is usually not strong enough to satisfy the requirements for the polarization control. Methods have been presented to achieve stronger CD. To the best of our knowledge, giant CD has been achieved in double layer CMMs or the achiral metal squares with non-normal incidence.[5–7,13] The fabrication of double layer or multilayer CMMs requires more precise alignment and complicated process technology. As for the achiral meta-materials, working at oblique incidence is not always convenient experimentally. Beyond this, the single layer CMM with giant CD is usually in the near infrared region.[17]
In this paper, we present a general approach to enhancing the CD signal from a 2D single CMM by adding a reflector layer behind the CMM, which is composed of periodic L-shaped meta-atoms in our case. The localized surface plasmonic resonance (LSPR) supported by the meta-atoms gives rise to the reflection difference between the RCP and LCP, where this effect is further amplified by the Fabry–Perot (FP) resonance formed between the two layers. Numerical results show that the CD maximum of the reflected light is enhanced by nine times compared with that of the single layer meta-atoms in the visible optical range. Further analysis of reflection efficiencies demonstrates that only one polarization component (RCP to RCP) exists near the resonance wavelength, indicating that a circular polarizer is realized which can reflect one circular polarization without changing its handedness and absorb the other. The analysis of relevant modes and detailed influence of the layer separation proves that the enhancement of the CD signal originates from the hybrid mode, which comprises the FP and the LSPR. Furthermore, the influence of the periodicity is also investigated. Our results present an easy and practical method to enhance the CD signal from single layer CMMs and to realize a reflective circular polarizer, which can find its applications in integrated photonics and biosensing. Particularly, wave propagation in Fabry–Perot cavity presents a spin-dependent splitting.[18] Additionally, the spin-dependent displacements between the chiral metamaterials can be enhanced at certain incident angles.[19] Combining the above advantages, the chiral effect in the Fabry–Perot cavity may provide a possible way to enhance the photonic spin Hall effect.
Figure
The complex transmission and reflection coefficient can be defined as 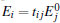
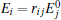
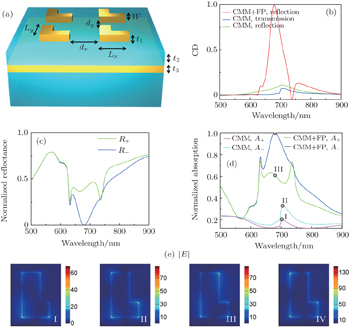
CD can be expressed as the difference in transmittance, reflectance, absorption,[6] or extinction cross section[21] between LCP and RCP. In our design, as the transmittance is almost zero, we are mainly concerned with the CD of reflectance which is calculated from
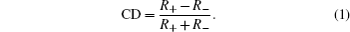
Figure
The comparison of absorption efficiency between the double layer and the single layer is shown in Fig.
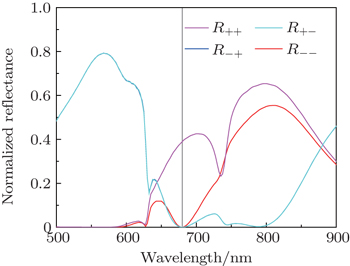
Although CD = 1 means that one circular polarization is absorbed completely by the structure, for another polarization, the co- and cross-polarization components may coexist, which is usually not wanted in application. Indeed, the coexistence of co- and cross-polarization components is common in the 2D CMMs except for those structures which are highly symmetric (for example, C4-symmetric).[22–24] The structure in our design is clearly anisotropic (not C4 symmetric), thus the corresponding reflection efficiencies should be noticed.
Figure
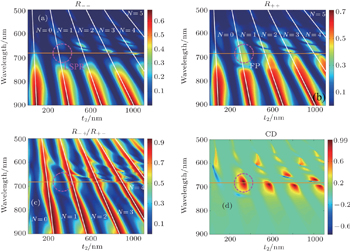
As the tailoring ability of FP cavity is from the radiation coupling[25] dependent on the cavity length, we present the reflection efficiency as a function of incident wavelength and spacer thickness n Fig.
The values of normalized efficiency R−−, for the thickness values of spacer spanning from 10 nm to 1100 nm are first studied in Fig.
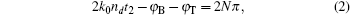
The efficiency R++ (in Fig.
As R−+ equals R+−, they have no contribution to the CD and are shown in Fig.
The CD septum is shown Fig.
As described above, near the purple circle, the efficiency R−− is zero due to the enhanced LSPR, while R++ is at the maximum due to the constructive interference. Additionally, the destructive interference condition is satisfied for the cross polarization component. So, according to formula (
The peculiar dips in Figs.
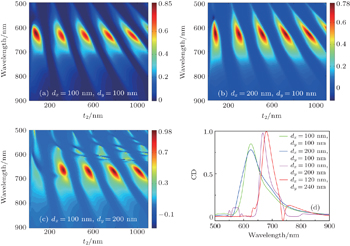
In this part, we numerically study the role of lattice spacing in the chiral response. The lattice arrangement is important for the CMMs as the chiral response can be induced for the achiral arrays by appropriately selecting lattice parameters.[29] As our structure is asymmetric (Lx ≠ Ly), we will observe different responses when lattice spacings are changed in different directions.[30]
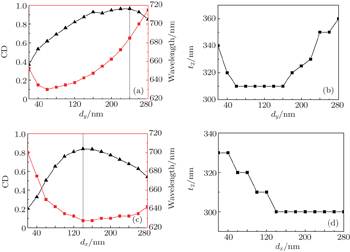
The response along the y direction is first studied by varying dy from 20 nm to 280 nm, where the dx is set to be a constant of 100 nm. In particular, we study the resonance chiral response near the t2 = 325 nm. Thus the resonance CD value, the resonance wavelength, and the spacer thickness at the resonance position are a function of dy each. The extracted data are shown in Figs.
The role of periodicity along the x direction is also studied in Figs.
From the above analysis, we can see that large dy is needed to obtain a strong chiral response, and the lattice parameters provide us with an additional degree of freedom for tuning chirality.
We provide the CD spectrum as a function of wavelength and spacer thickness in Fig.
The peculiar dips are present only in Fig.
From the analysis of the lattice spacing, we can see two things. The first thing is that to tune the asymmetric MM response effectively, we can start from tuning the in-plane coupling along the direction which significantly affects the chiral response. The second thing is that to obtain a huge CD, how to optimize the parameters (dx/dy) is important.
In this work, we numerically demonstrate that a huge 2D chiroptical response in the visible band can be obtained by combining the advantages of Fabry–Perot microcavities and 2D CMMs array. The analysis of reflection efficiencies demonstrates that our design can be used as a circular polarization device which can reflect one circular polarization without changing its handedness, and absorb the other. The method of the cavity enhanced chiral response is general. The asymmetric behavior as a function of direction is studied. This analysis also demonstrates an additional degree of freedom for tuning the chirality of asymmetric MMs via varying lattice parameters. Moreover, our design can ease the fabrication requirements such as the precise alignment and high cost in the multi layer MMs.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 |