Cite this Article
Zhou Meiling, Peng Yulian, Chen Chidao, Chen Bo, Peng Xi, Deng Dongmei. Interaction of Airy–Gaussian beams in saturable media. Chinese Physics B, 2016, 25(8): 084102  
Permissions
Interaction of Airy–Gaussian beams in saturable media
Zhou Meiling1, Peng Yulian1, Chen Chidao1, Chen Bo1, Peng Xi1, Deng Dongmei1, 2, †,
Guangdong Provincial Key Laboratory of Nanophotonic Functional Materials and Devices, South China Normal University, Guangzhou 510631, China
CAS Key Laboratory of Geospace Environment, University of Science & Technology of China, Chinese Academy of Sciences (CAS), Hefei 230026, China

 

† Corresponding author. E-mail: dmdeng@263.net

Project supported by the National Natural Science Foundation of China (Grant Nos. 11374108 and 10904041), the Foundation for the Author of Guangdong Province Excellent Doctoral Dissertation (Grant No. SYBZZXM201227), and the Foundation of Cultivating Outstanding Young Scholars (“Thousand, Hundred, Ten” Program) of Guangdong Province, China. CAS Key Laboratory of Geospace Environment, University of Science and Technology of China.

Abstract
Abstract

Based on the nonlinear Schrödinger equation, the interactions of the two Airy–Gaussian components in the incidence are analyzed in saturable media, under the circumstances of the same amplitude and different amplitudes, respectively. It is found that the interaction can be both attractive and repulsive depending on the relative phase. The smaller the interval between two Airy–Gaussian components in the incidence is, the stronger the intensity of the interaction. However, with the equal amplitude, the symmetry is shown and the change of quasi-breathers is opposite in the in-phase case and out-of-phase case. As the distribution factor is increased, the phenomena of the quasi-breather and the self-accelerating of the two Airy–Gaussian components are weakened. When the amplitude is not equal, the image does not have symmetry. The obvious phenomenon of the interaction always arises on the side of larger input power in the incidence. The maximum intensity image is also simulated. Many of the characteristics which are contained within other images can also be concluded in this figure.

PACS: 41.85.–p;42.25.Bs;42.65.Jx
Keyword:Airy–Gaussian beam;interaction;saturable media
1. Introduction

In 1979, Berry and Balazs theoretically described the theory for the first time in the context of quantum physics that the Airy wave packet is one of the solutions of the Schrödinger equation (SE).[1] The Airy beam possesses many attractive and significative properties. The extraordinary properties, such as self-healing,[2] self-bending,[3] and diffraction free,[4] have been made sure. It is a non-spreading wave packet that contains infinite energy and remains invariant during propagation. The initial Airy function is not realizable in practice. So, Siviloglou et al.,[3] and Siviloglou and Christodoulides[4] by using different methods discussed the Airy optical beam which retains a finite energy for the first time in 2007. The Gaussian beam also has been studied in different cases. The nonparaxial propagation of phase-flipped Gaussian beams[5] have been discussed by Gao. The propagation factor and the kurtosis parameter of a Gaussian beam with vortex[6] also has been reported in 2012. An Airy–Gaussian (AiG) beam, which can be considered as an Airy beam carried with finite energy passes through the Gaussian aperture, is described in more practical propagation. Also, AiG beam still retains the diffraction free characteristic within a finite propagation distance. In 2007, Bandres and Gutierrez-Vega demonstrated that generalized AiG beams can be propagated through an ABCD optical system, in free space and a quadratic index medium.[7] In 2009, Novitsky studied the nonparaxial Airy beams.[8] Two years later, Rudnick analyzed Airy–soliton interactions in Kerr media.[9] Wiersma discussed the optical waveguide structure of an Airy beam under certain conditions by using numerical analysis method[10] in 2014. In addition, the optical bullet of an Airy beam[11] and other cases of Airy beams[12–19] have been widely researched since it was discovered.

In the nonlinear (NL) media, the accelerating beam has been studied extensively in recent years.[20–23] The effect of the saturable nonlinearity results in a dependence of the refractive index on the light intensity. As an important optical NL effect, there have been many investigations on saturable nonlinearity[24–29] for so many years. The effect of the saturable nonlinearity revealed the importance for all-optical applications. AiG beams are of both fundamental and technological importance if they are in saturable media.

However, there are few papers investigating the interaction of two AiG beams. So, in this paper, after introducing NL SE under the paraxial approximation, we derive the general form of the incident beam which is composed of two AiG beams with a relative phase between them. Under the condition of the same amplitude, the interactions of two AiG components with different intervals and distribution factors are introduced in the in-phase case and the out-of-phase case. We also simulate the relationship between the maximum intensity and the transmission distance. Subsequently, we analyze the influence of the distance, the phase and the distribution factor on the interaction of different amplitudes, and finally the comparison is made.

2. Theoretical analysis

Under the paraxial approximation, the normalized NL SEs for the evolution of a slowly varying envelope ψ of the beams’ electric field are depicted as[30,31]

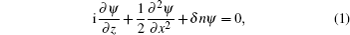
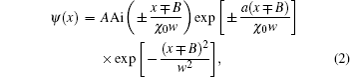
where x and z represent the dimensionless transverse coordinate and the propagation distance, respectively, δn is the NL change in the index of refraction. According to the standard theory of the photorefractive effect, the saturable nonlinearity in the form δn = |ψ|2/(b + |ψ|2), where 0 < b ≤ 1, represents a saturation argument that is taken to be 1 in this article. Generally speaking, for an AiG beam, the initial field distribution can be written as

where A and B represent the amplitude and the interval factor, w represents the width of beam, 0 ≤ a <1 is an arbitrary decay constant. χ0 is the distribution factor that makes the beam gravitate towards an Airy beam when it is a low value or a Gaussian beam when it is a high value.

We have shown the single beam solutions in Eq. (2). In fact, due to the wide application of multimode optical fiber, we need to consider the interaction between the beams. However, there is little investigation into the interaction of two AiG beams. So, we want to investigate their interactions. The incident beam is composed of two AiG beams with a relative phase between them, it reads as

in which Q is the argument which controls the phase shift. In the case of Q = 0, the two components are in-phase; in the case of Q = π, they are out-of-phase. In this paper, we only pay attention to these two cases. In our calculations, the influences of various parameters on the beams’ interactions are discussed. Now, we present different situations in the following section.

3. Simulation results

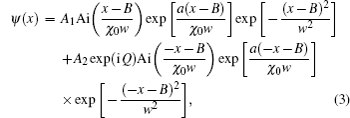
In this section, we give simulation results based on Eq. (2) to show the interaction of the two AiG components. When there is a large distance between AiG components in the incidence leading to a weak interaction, we only show the case of the relatively small distance.

3.1. The same amplitude for two AiG components

Under the condition of A1 = A2, we study the two kinds of events of the incidence: in-phase and out-of-phase. The corresponding results are shown in Fig. 1 and Fig. 2, respectively.

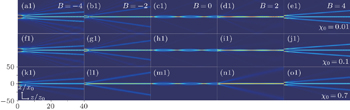Fig. 1. The interaction of two AiG beams with different values of B and χ0 for A1 = A2 = 4 and Q = 0.
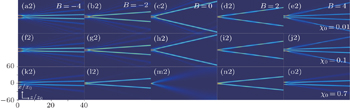Fig. 2. The interaction of two AiG beams with changing the values of B and χ0 for A1 = A2 = 4 and Q = π.

For the in-phase case, figure 1 shows the influence of the different intervals and distribution factors on the interaction of the AiG beams. The interaction between the two AiG components is attraction. The two components form the quasi-breathers on the main lobe after shedding some radiation. It is noted that the smaller the absolute value of the interval between the two AiG beams, the weaker the side lobe intensity, and the bigger the angle between the side lobes. At the same time, in the course of the above changes, even though the number of the quasi-breathers is decreasing, the phenomenon of quasi-breathers is more obvious. In other words, the smaller the distance is, the stronger the attraction is. These phenomena are shown in each line in Fig. 1. When χ0 increases, the phenomena of the quasi-breather and the self-accelerating of the two AiG components are weakened. These phenomena are revealed in each column in Fig. 1. The reason is that when the distribution factor is increased, the characteristic of AiG beam is close to the characteristic of the Gaussian beam, and the characteristic of the Airy beam is reduced. So, the distribution factor affects the strength of the quasi-breather and the self-accelerating in the intensity images indirectly.

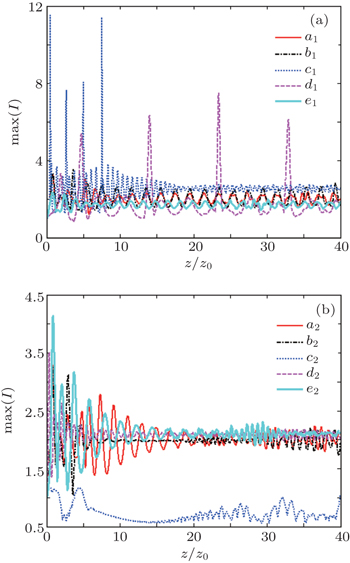
Concerning the case of out-of-phase, the relevant outcome is shown in Fig. 2, which shares the same numerical parameters as the in-phase case. We can find that, compared to Fig. 1, the biggest difference is the formation of repulsive quasi-breather pairs. From the intensity images in Fig. 2, the influence of the interval on the intensity, the angle between beams, and the interaction strength is the same as in the case of in-phase. The main lobe almost had no diffraction of transmission, except in Fig. 2(m2). It is the result of the interaction of B and χ0. One can see that the quasi-breather or quasi-breather pairs, as well as shedding radiation, move along straight lines from Fig. 1 and Fig. 2.

The maximum intensities versus the propagation distance are demonstrated in Fig. 3. Many of characteristics contained in Fig. 1 and Fig. 2 can also be concluded in Fig. 3. For example, the regularity that is first divergence and then convergence can also be observed in the maximum intensities for each case oscillating with the propagation distance. More directly, the rule of the intensity of the interaction can be summed up directly from the coordinate of the graph.

Fig. 3. The maximum intensities of beams shown with curves a–e versus propagation distance, curves a1–e1 in panel (a) correspond to those in Fig. 1, respectively, and curves a2–e2 in panel (b) correspond to those in Fig. 2, respectively.
3.2. The amplitude of the two AiG components is different

Figure 4 shows the influence of the different amplitudes and distribution factors on the interaction of the AiG beams. In calculations, the interval between the beams is taken as −4 and A1 is 5 in Figs. 4(a3)–4(o3). In the process of the A2 from 2 to 10, the phenomenon of the quasi-breathers and the intensity of the side lobe are first increased and then decreased. These phenomena are most obvious when A1 and A2 are close. The main lobe is always close to the stronger intensity of the incident beam. The effect of the change in the distribution factor on the phenomena of the quasi-breather and the self-accelerating is very similar to Fig. 1. Comparing Fig. 1 with Fig. 4, the amplitude of the two AiG components is the same as that in Fig. 1, but is not in Fig. 4. So, the primary difference between Fig. 1 and Fig. 4 is whether it takes on symmetry or not with regard to x/x0 = 0.

Fig. 4. The interaction of two in-phase AiG beams with the same B for different χ0 and A, (a3)–(e3) and (p3) χ0 = 0.01, (f3)–(j3) and (q3) χ0 = 0.1, (k3)–(o3) and (r3) χ0 = 0.5.

Figure 5 shows the interaction of the different distance of the two incident beams which have different energies. In this figure, each row and each column indicate the influence of the interval factor and the amplitude on the interaction. Therefore, the side lobe of each row in Figs. 5(a1)–5(l1) is similar to the variation characteristic of the side lobe of each line in Fig. 1, it is shown that the smaller the interval is, the bigger the angle between the side lobe and the smaller the intensity of the side lobe is. In each column of Figs. 5(a1)–5(l1), the main lobe carries out a repeat process: divergence and convergence, then form quasi-breathers. The repeat process can be shown by the regular change of the maximum intensity in Fig. 5(m1). The feature is analogous to each row when B changes from −2 to 1. When B equals 1, the beam is the most divergent. As B equals 2, as depicted in Figs. 5(e1), 5(k1), the side lobes are almost lost, and the energy of the main lobe is the most concentrated. The feature can also be found in Fig. 5(m1), the maximum intensity of B = 2 is the biggest. Why are these special phenomena not appearing in the special position of B = 0? It is because the main lobe of the input beam is not in the position of the x/x0 = 0 when the B = 0. As B continues to grow to 3, as displayed in Figs. 5(f1), 5(l1), the intensity of the side lobe is enhanced and the main lobe is weakened, but all of them have the generation of quasi-breathers. But the intensities are not the same in both sides of the main lobe, all of them are inclined to one side of the incident AiG beam that possesses stronger intensity. Its energy is essentially unchanged. The added energy in the incident beam adds up to the side lobe after interaction.

Fig. 5. The interaction of two (a1)–(l1) in-phase and (a2)–(l2) out-of-phase incident AiG beams for different B and A2, (m1), (m2) maximum intensities of beams in curve a–curve e versus propagation distance.

As for the out-of-phase and unequal case, this is displayed in Figs. 5(a2)–5(l2). The regularity of the angle, the intensity of the side lobe, as well as the interaction in each row of Figs. 5(a2)–5(l2) is quite similar to each line in Fig. 2. As compared to Fig. 2, the input intensity is constantly changing, so the characteristics of the intensity variation on the main lobe in Figs. 5(a2)–5(l2) are not the same as in Fig. 2. The intensity of the two main lobes is not equal, the intensity of the main lobe on the side of the larger input intensity is larger. In Fig. 5(m2), the value of the maximum intensity reflects the change of the intensity on the main lobe; the regular change of the maximum intensity shows the formation of quasi-breathers.

4. Conclusion

In conclusion, the interaction of AiG beams in the incidence is reported in saturable media. The feature that the attraction of beams in the in-phase and the repulsion in the out-of-phase has been laid down, regardless of A1 and A2. The interaction of two AiG components increases as the interval B decreases. The major difference between the same and different A is whether it has a symmetry or not. However, if A1 and A2 have the same value, the variety of quasi-breathers is opposite between the in-phase case and the out-of-phase case. As the amplitude is not equal, the more evident phenomenon of the interaction always appears at the side of stronger input energy in the incidence. Then we plot the maximum intensity as the change of transmission distance. From the figures, one can see many of the same phenomena occurred as given above.

Reference
1Berry M VBalazs N L 1979 Am. J. Phys. 47 264
2Broky JSiviloglou G ADogariu AChristodoulides D N 2008 Opt. Express 16 12880
3Sivilogou G ABroky JDogariu AChristodoulides D N 2007 Phys. Rev. Lett. 99 213901
4Siviliglou G AChristodoulides D N 2007 Opt. Lett. 32 979
5Gao Z HLv B D 2008 Chin. Phys. 17 943
6Zhou G Q2012Acta Phys. Sin.61(in Chinese)174102
7Bandres M AGutierrez-Vega J C 2007 Opt. Express 15 16719
8Novitsky A VNovitsky D V 2009 Opt. Lett. 34 3430
9Rudnick AMarom D M 2012 Opt. Express 19 25570
10Wiersma NMarsal NSciamanna MWolfersberger D2014Opt. Lett.1395997
11Abdollahpour DSuntsov SPapazoglou D GTzortzakis S 2010 Phys. Rev. Lett. 105 253901
12Deng DLi H 2012 Appl. Phys. 106 677
13Deng D M 2011 Eur. Phys. J. D 65 553
14Chen C DChen BPeng XDeng D M 2015 J. Opt. 17 035504
15Ez-Zariy LHennani SNebdi HBelafhal A 2014 Opt. Photon. 4 325
16Zhou Y MZhou G QRu G Y 2014 Prog. Electromagn. Res. 40 143
17Deng X BDeng D MChen C DLiu C Y 2013 Acta Phys. Sin. 62 174201 (in Chinese)
18Yariv AYeh P1984Optical waves in crystalsNew YorkWiley
19Chen H C1983Theory of electromagnetic wavesNew YorkMcGraw-Hill
20Hu YHuang SZhang PLou C BXu J JChen Z G 2010 Opt. Lett. 35 3952
21Kaminer ISegev MChristodoulides D N 2011 Phys. Rev. Lett. 106 213903
22Dolev IKaminer IShapira ASegev MArie A 2012 Phys. Rev. Lett. 108 113903
23Bekenstein RSegev M 2011 Opt. Express 19 23706
24Enns R HEdmundson D ERangneker S SKaplan A E 1992 Opt. Quantum Electron. 24 1295
25Edmundson D EEnns R H 1995 Phys. Rev. 51 2491
26Edmundson D E 1997 Phys. Rev. 55 7636
27Desyatnikov A SMihalache DMazilu DMalomed B ALederer F 2007 Phys. Lett. 364 231
28Zhang Y QBelic MWu Z KZheng H BLu K QLi Y YZhang Y P 2013 Opt. Lett. 38 4585
29Zhang Y QBelic MZheng H BChan H XLi C BLi Y YZhang Y P 2014 Opt. Express 22 7160
30Boyd R W2008Nonlinear Optics3rd edn.AmsterdamAcademic Press
31Zhang YSkupin SMaucher FPour A GLu KKrolikowski W 2010 Opt. Express 18 27846