† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61372034).
We report a polarization beam splitter based on phase gradient metasurface for microwave frequency region. The metasurface is constructed by anisotropic cells with independent phase response for differently-polarized waves. Through putting different gradient phases for orthogonally-polarized waves on a focusing metasurface, the anisotropic sample has the ability to enhance gain and split orthogonally-polarized waves. The simulation results indicate that the incident spherical waves are converted into plane waves and split into an x-polarized wave with a refraction angle of −24° and a y-polarized wave with a refraction angle of 37.6° in the y direction. For verification, a metasurface sample with a size of 102.5 mm ×102.5 mm is fabricated and measured. The consistence between numerical and experimental results validates the improved gain of 10.5-dB against the feed source and the splitting effect. Moreover, the thickness of the proposed metasurface is 3 mm which is ultra-thin against the wavelength at 15 GHz. The proposed prescription opens a new route to the applications of anisotropic metasurface in microwave band.
Metamaterials (MTMs) have a strong ability to manipulate electromagnetic (EM) waves on a subwavelength scale, resulting in fascinating effects such as negative refraction, superimaging/hyperimaging, and anomalous reflection/refraction.[1] A special class of MTM, namely, two-dimensional (2D) metamaterial, also called metasurface, has drawn tremendous attention recently due to extraordinary flexibility to tailor the EM wave and the ease of on-chip fabrication due to its planar profile.[2–5] Meanwhile, research on metasurfaces explosively expanded from optics to microwave[6–8] in recent years, especially on gradient metasurface (GM)[9–11] and planar focusing metasurface (PFM).[12–15] For example, by employing V-shaped antennas in a metasurface, the GM and the general reflection/refraction laws were first proposed by Yu et al. in Ref. [1]. Then the PFM was demonstrated and analyzed by adopting I-shaped antennas in Ref. [2]. By employing GM, the mutual high-efficiency conversion between surface-plasmon-like mode and spatial radiated mode was demonstrated in Refs. [3] and [16]. More recently an anisotropic gradient metasurface was perfectly shown in Ref. [17]. Even so, compared with the research on isotropic metasurface, little work on anisotropic metasurface has been published, which still restricts the controlling of the differently-polarized waves.[18,19]
Among the research on anisotropic metasurface, an essential research topic is to manipulate orthogonally-polarized waves independently. For instance, by using a Huygens metasurface the independent controls of orthogonally-polarized transmitted waves are realized in Ref. [20]. By employing anisotropic phase element, the transparent polarization beam splitter is also achieved in Ref. [21]. But note that references [20] and [21] both focused on the polarization beam splitters irradiated by plane waves. Therefore a new way to realize the beam splitter irradiated by spherical waves is still greatly desired. In this paper we first propose an anisotropic refraction metasurface cell, which can manipulate the x/y-polarized refraction waves independently. Then an anisotropic transmitting metasurface is designed and fabricated. Three cases are discussed according to differently-polarized incident waves. The results demonstrate that the spherical waves emitted from the patch antenna have been converted into plane waves and refracted to different directions according to different polarization states.
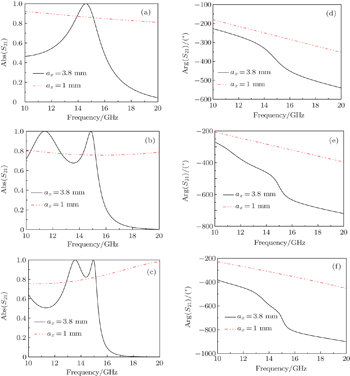
The structure of the metasurface cell is depicted in Fig.
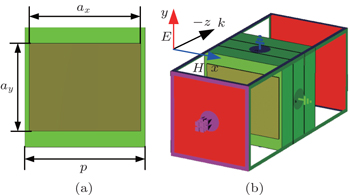 | Fig. 1. (a) Top view of the metasurface cell, (b) the perspective view and the simulated setup of the metasurface cell. |
The anisotropic transmitting metasurface is designed based on a focusing metasurface. Here we set the focal length to be 30 mm and first demonstrate the designing principle prior to simulations and experiments. According to the general refraction law as given below
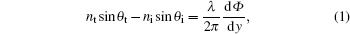
Moreover, considering the fact that the spherical waves can be converted into plane waves by PFM effectively, we can put an extra gradient phase on the PFM lens to obtain the plane waves converted by spherical waves refracted to an anomalous angle. Furthermore, if we put different gradient phases for x/y-polarized waves on the PFM lens, the spherical waves will be split into x/y-polarized plane waves with different refraction angles. According to this point, the phase distributions for x/y-polarized incident waves should meet the phase relationship as described as follows:
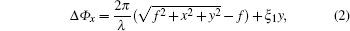
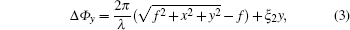

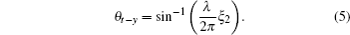
According to the above designed principle, we propose a PFM with independently controlling the differently-polarized waves as shown in Fig.
 | Fig. 4. (a) Top view of the proposed PFM, (b) the relative phases of x-polarized waves distributed on the PFM, and (c) the relative phases of y-polarized waves distributed on the PFM. |
We first simulate a patch antenna with good performance at 15 GHz, which is adopted to act as a feed source. Figures
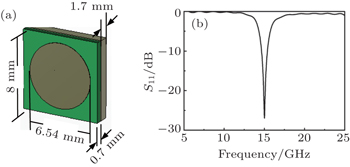 | Fig. 5. (a) Patch antenna acting as the feed source of the PFM and (b) the return loss of the patch antenna. |
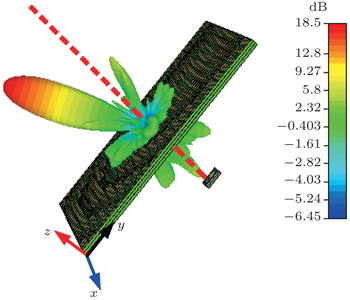 | Fig. 7. Far-field pattern of the anisotripic metasurface system under the irradiation of x-polarized waves. |
Similarly, we set the polarized direction of the patch antenna to be along the +y axis. With the same simulated setup, the 3D far-field pattern of the anisotropic metasurface is calculated in CST 2011, and the results are shown in Fig.
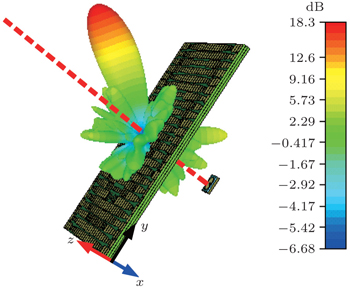 | Fig. 9. Far-field pattern of the anisotropic metasurface system under the irradiation of y-polarized waves. |
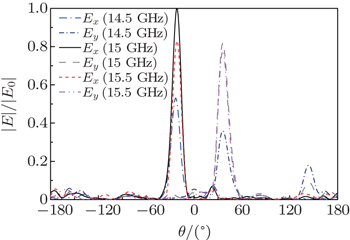
In order to obtain both x/y-polarized incident waves at the same time, the patch antenna is set to be oblique in xoy plane as shown in Fig.

Figure
 | Fig. 12. 3D far-field pattern of the anisotropic metasurface system under the irradiation of x/y-polarized incident waves. |
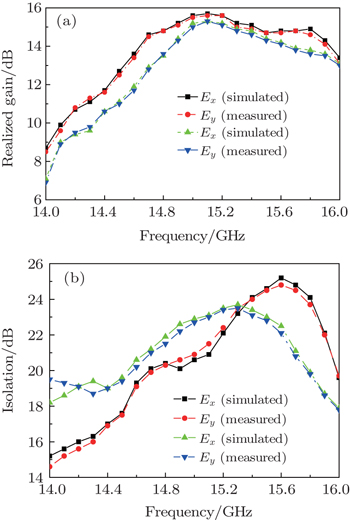
In order to further verify the designing principle, we fabricate a PFM sample with a size of 102.5 mm×102.5 mm by using conventional printed circuit board (PCB) technique. Concrete parameters are consistent with the PFM we have simulated above as shown in Fig.
 | Fig. 15. Simulated and measured far-field radiation patterns at 15 GHz of the anisotropic metasurface system with x/y-polarized incident waves. |
In this work, we demonstrate an utra-thin beam splitter through using anisotropic metasurface. By putting different gradient phases of x/y-polarized waves on a PFM, we also show a new designing principle of anisotropic metasurface. Both simulated and measured results demonstrate great improvements of the patch antenna gain and perfect beam splitting effect, which possesses great application values in the anisotropic devices, high gain antennas, lens, etc.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 |