† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11374004), the Science and Technology Development Program of Jilin Province, China (Grant No. 20150519021JH), the Fok Ying Tung Education Foundation, China (Grant No. 142001), and the Support from the High Performance Computing Center (HPCC) of Jilin University, China.
5f-elements encaged in a gold superatomic cluster are capable of giving rise to unique optical properties due to their hyperactive valence electrons and great radial components of 5f/6d orbitals. Herein, we review our first-principles studies on electronic structures and spectroscopic properties of a series of actinide-embedded gold superatomic clusters with different dimensions. The three-dimensional (3D) and two-dimensional (2D) superatom clusters possess the 18-electron configuration of 1S21P61D10 and 10-electron configuration of 1S21P41D4, respectively. Importantly, their electronic absorption spectra can also be effectively explained by the superatom orbitals. Specifically, the charge transfer (CT) transitions involved in surface-enhance Raman spectroscopy (SERS) spectra for 3D and 2D structures are both from the filled 1D orbitals, providing the enhancement factors of the order of ∼ 104 at 488 nm and ∼ 105 at 456 nm, respectively. This work implies that the superatomic orbital transitions involved in 5f-elements can not only lead to a remarkable spectroscopic performance, but also a new direction for optical design in the future.
Gold nanoparticles exhibit strong d–s hybridization and relativistic effects which results in a wide variety of optical phenomena. These properties have attracted a huge interest in the optical studies of bimetallic nanoparticles.[1–4] On the other hand, the spectroscopic properties of actinide also play a remarkable role in the regular arrays of metals.[5–10] The absorption and/or emission lines of 5f valence shell electrons are narrow and sharp in the visible range,[10–12] and these spectra lines could be hardly influenced by the external coordination environment.[5,9] Consequently, the superatom model comprised of f-block and ds-block elements could be envisioned to very likely carry a revolutionary spectroscopic performance.
One of the first superatomic experiments was the seminal work of Knight et al. in 1984.[13] They observed conspicuous peaks in the mass spectra of Na clusters containing 2, 8, 20, 40, … atoms. The electrons in Na [3s1] clusters are confined in quantized orbitals 1S2, 1S2 1P6, 1S2 1P6 1D10 2S2 1S2 1P6 1D10 2S2 1F14 2P6, …, respectively, and successive electronic shell closure accounts for the enhanced stability of the magic clusters. Subsequent mass spectra of other simple homo- as well as heteroatomic metal clusters have confirmed the relationship between electronic shell closure and enhanced stability.[14] Currently, the electronic structures and derived properties of stable bimetallic gold-based clusters can also be modeled via the superatom models.[14–18] The first predicted superatomic cluster was the icosahedral W@Au12 based on density functional theory (DFT) involving the 18-electron count (1S21P61D10),[19] which was later confirmed via photoelectron spectroscopy (PES).[20] Soon after that, a series of bimetallic gold superatom models (M@Aun), where M is a d-block atom, have been proposed theoretically.[21–25] Among them, these superatomic clusters all possess a great advantage compared with the pure gold clusters in tuning the excitation light,[26–36] which has been identified on the experimental study.[37–40] Besides, also such as one- and two-photon optical absorption,[41,42] circular dichroism,[43–45] electron paramagnetic resonance spectra,[46] etc. All these optical phenomena can be effectively explained by superatom models.
As is well known the f-block elements have a high density of electronic states, because of their hyperactive valence electrons. This particular attribute has led to an intense interest in optics and magnetic fields in applications of f-element-embedded gold clusters, such as Ac@Au7,[7] Sg@Au12,[47] An@Au14 (An = Ac, Th, Pa, U),[8,48] Gd@Au15,[49] etc. Specific optical characteristics of these superatom models were obtained through their structural and compositional modifications.[26–34] The relevant modification produces spectral shifting in a very wide range that is even as important as the morphological modification in one-component nanoparticles.[50] As reflections of electronic structures, spectroscopic studies of actinide–gold systems that focus on molecular excited-state properties promise our further understanding of actinide–gold bonding schemes and 5f-element electronic structures.
Although in the past several decades much effort has been made to produce and model gold-based bimetallic systems, the understanding of their fascinating properties in the combination systems of ds- and f-elements is still in its infancy. In this paper, we give a concise review of our recent first-principles calculations on electronic structures and spectroscopic properties of actinide-embedded gold superatom models and their recent progress. In Section 2, we demonstrated possible methods to deal with heavy metal clusters that contain ds and f-electrons. In Section 3, we analyze the electronic structures and spectroscopic properties of one-dimensional (1D), two-dimensional (2D), three-dimensional (3D) models, and list the specific molecular orbitals (MOs) that are associated with the corresponding absorption spectra. Finally, a brief conclusion and perspectives on these superatom models are presented in Section 4.
There are some theoretical challenges associated with studying heavy metal clusters.[51–54] Firstly, quantum calculation involving a large number of electrons is computationally extremely challenging, in addition, strong relativistic effects must be considered for each heavy atom. In this review, the electronic structures and spectroscopic properties of actinide-embedded gold superatom models were calculated by using DFT and time-dependent DFT (TDDFT) with relativistic effective core potential (RECP) approach,[55–59] respectively. A significant advantage of these methods is that for systems containing heavy metal elements, the electron correlations can be handled effectively without significantly increasing the computational cost.[60–62] Meanwhile, the RECP approach can effectively consider the scalar relativistic effects, which is crucial for describing the behaviors of ds- and f-electrons.[63] Moreover, because the spin–orbit coupling (SOC) effects play an important role in the excited-state calculation of medium-sized gold clusters,[64–67] the SOC effects within the framework of zero-order regular approximation (ZORA) were also considered in the following calculations.
Absolute Raman intensities are presented as the differential Raman scattering cross-section (DRSC). For Stokes scattering with an experimental setup of a 90° scattering angle and perpendicular plane-polarized light, the cross-section is given as[68]
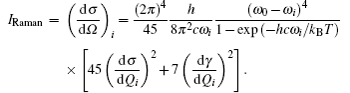
These superatom models of actinide-embedded gold clusters can be expressed by a formula
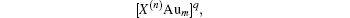
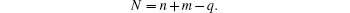
If N corresponds to a magic number (2, 8, 18, 34, 58, etc.) commonly linked with electronic stability, the superatom complex may be particularly stable. When N is not equal to one of these magic numbers, the complex is expected to have a different structure instead of a spherical one.[65]
Currently, doped gold clusters have become a subject of high interest research because of their stable physicochemical activities and unique geometric structures.[70,71] The interactions between the encapsulated atoms and gold clusters allow fine tuning the formations of nanoparticles agglomerates, resulting in more compact structures with lower energy.[72–74] Among them the endohedral gold clusters encapsulating a foreign atom (such as W@Au12) have been formed under specific experimental conditions,[19] and the theoretically calculated value (2.02 eV) of electron affinity (EA) is in good agreement with the experimental data (2.08 ± 0.02 eV). Thus, in order to facilitate future experimental validation, we also calculated the EA values of Th@Au14 and U@Au14 clusters. These EA values are at least 2.35 eV, which is higher than 2.02 eV, suggesting a thermodynamically more stable state of Th@Au14 than that of W@Au12.
In order to understand the electronic structure requirements of actinide-embedded gold superatom models the MO energy diagrams of the ground states of Th@Au14, [Ac@Au14]−, [Pa@Au14]+, Pa@Au14, U@Au14 are shown in Fig.
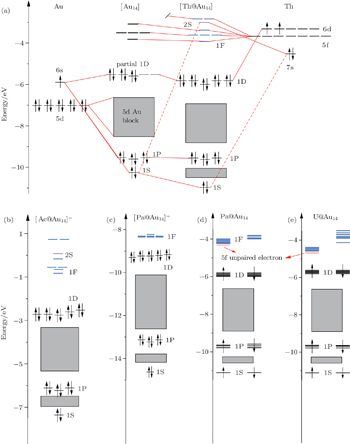 | Fig. 1. MO energy diagrams of the ground state of (a) Th@Au14, (b) [Ac@Au14].−, (c) [Pa@Au14]+, (d) Pa@Au14, (e) U@Au14. In panel (a), solid red lines denote the major contributions to the respective MOs, while dashed red lines represent the minor contributions. In panels (d) and (e), the red transverse lines represent occupied molecular orbitals. Upper-case and lower-case letters represent the superatomic and atomic orbitals, respectively. Adapted with permission from Ref. [8]. Copyright 2016 Springer. |
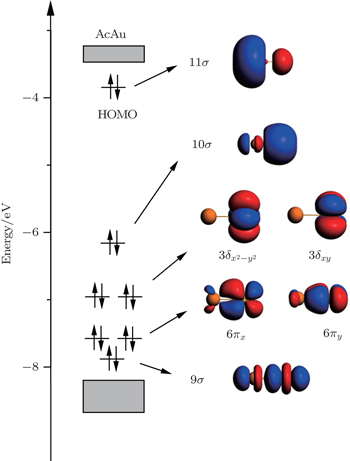
As is well known the inherent relativistic effects of the gold clusters can cause apparent hybridization between the inner-shell d orbitals and the outer-shell s orbitals (these hybrid orbitals are named 5d6s orbitals). When foreign atoms are embedded, hybridization becomes more apparent between 5d6s orbitals and the valence electron orbitals of the doped atoms.[19,54] So the formation of Th@Au14 cluster (Th: 6d27s2) mainly involves the interaction between the hybrid atomic orbitals of Th and the gold cage orbitals of the polyhedron, namely 1S-Au14 (with 2 electrons), 1P-Au14 (with 6 electrons), 1D-Au14 (with 6 electrons) (see Fig.
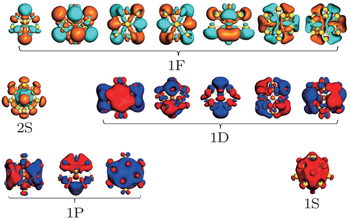 | Fig. 2. Superatomic jelliumatic MOs of the ground state of Th@Au14 (isodensity = 0.02 a.u.). Adapted with permission from Ref. [8]. Copyright 2016 Springer. |
In addition, we also compare the electronic structures of the isoelectronic clusters [Ac@Au14]− and [Pa@Au14]+ (Ac: 6d17s2; Pa:5f26d17s2), which all satisfy the 18-electron configuration of 1S21P61D10 jellium state (see Figs.
It should be noted that for highly symmetric clusters, Jahn–Teller (JT) distortions become operative in some cases because of the interelectronic repulsion caused by vibronic interactions.[76,77] (e.g., splitting of t2u orbitals via JT distortion under Oh symmetry). As a result, the optimized D2d structure of [Ac@Au14]− is very similar to that of Th@Au14, the [Pa@Au14]+, Pa@Au14, and U@Au14 analog instead adopt a C1 symmetry. This difference can be attributed to the sizes of the four actinide metal atoms: namely, Ac, 1.86; Th, 1.75; Pa, 1.69 Å, and U, 1.70 Å.[78] In the Th@Au14D2d cluster, inclusion of the SOC effects causes the Th–Au bond length to be shortened by ∼ 0.2 Å in comparison with that obtained by including the scalar relativistic effects. Furthermore, the HOMO–LUMO (highest occupied molecular orbital–lowest unoccupied molecular orbital) gap value also decreases from 1.92 eV to 1.82 eV (see Fig.
 | Fig. 3. MO diagrams for the Th@Au14 cluster including relativistic effects with (right) and without (left) spin–orbit couplings. Adapted with permission from Ref. [8]. Copyright 2016 Springer. |
In fact, the superatom models are also generalized to the 2D planar structures.[73,79] The preference of planar structure is attributed to the relativistic effects that cause the size of the 6s orbitals to shrink and thus enhances the s–d hybridization. Taking the Ac@Au7 cluster as a framework, the Au7-D7h ring has a nearly cylindrical symmetry (see Fig. 
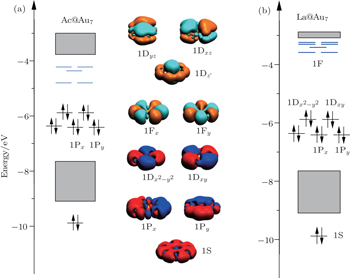 | Fig. 4. MO energy diagrams of the ground state of (a) Ac@Au7 and (b) La@Au7, and the superatomic jelliumatic MOs of Ac@Au7 cluster. |
The average total binding energies of per atom and HOMO–LUMO gap for Ac@Au7 are 2.70 eV and 2.42 eV respectively, and those for La@Au7 are 2.79 eV and 2.35 eV respectively. In general, nanocluster structures with binding energy greater than 2.40 eV and HOMO–LUMO gap larger than 1.70 eV are commonly regarded as being stable.[21] Therefore, our current results suggest that Ac@Au7 and La@Au7 both belong to stable structures.
For the 1D diatomic clusters, our previous work[33,34] based on DFT calculations has pointed out that the presence of the heteronuclear metal atoms can modify the electronic structures and electronic absorption spectra of binary coinage metal clusters. The binary coinage metal clusters also have great advantages in tuning the excitation light for SERS spectra compared with the pure element clusters. Thus, in order to explore the role of 5f-element in the actinide–gold dimer, we studied the Ac–Au molecule.
The actinium and gold atoms have the valence electronic configurations of 6d17s2 and 5d106s1 respectively. The lowest energy state of AcAu dimer is predicted to be singlet (see Fig. 
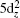
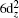
For the particular clusters, the electronic absorption spectrum is often used to identify the validity of the superatom model, because the allowed transitions involve mainly the superatomic (jelliumatic) orbitals in a low-energy range.[65,84,85] Thus, based on the above discussion on the electronic structures of actinide-embedded gold superatom models, we further analyzed the absorption spectra of pyridine-Th@Au14 complexes as shown in Fig.
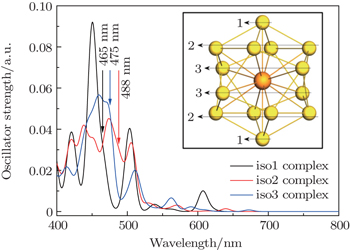 | Fig. 6. Absorption spectra of the pyridine-Th@Au14 complex at three different adsorption sites. The three different colored lines (1, 2, 3) denote three coordination types of the gold atoms (iso1, iso2, and iso3), serving as prospective adsorption sites for pyridine molecules in unit SERS study. Absorption coefficients are given as the oscillator strength in unit a.u. and wavelength in nm. Spectra were broadened by Lorentzian function with a width of 15 cm−1. Adapted with permission from Ref. [8]. Copyright 2016 Springer. |
In order to thoroughly understand the interaction between the molecule and the metal, we first listed the well-known six vibrational modes and corresponding frequencies of the pyridine molecule, namely, ring deformation modes (∼ 598 cm−1), ring breathing modes (∼ 978 cm−1 and ∼ 1021 cm−1) and ring stretch vibrational modes (∼ 1205 cm−1, ∼ 1468 cm−1, ∼ 1568/1574 cm−1), which all have exhibited very strong signals in SERS experiment.[89,90] The static Raman scattering spectrum of pyridine is mainly dominated by ring breathing and ring stretch modes. The relative Raman intensities of these vibrational modes are closely related to the adsorption site of pyridine molecule. For the three pyridine-Th@Au14 complexes (gold atoms possess three kinds of coordination types, see the inset in Fig.
Next, based on the typical CT resonance excitations, the SERS spectra ranging from 300 cm−1 to 1800 cm−1 for three typical pyridine-Th@Au14 complexes were simulated, as shown in Fig.
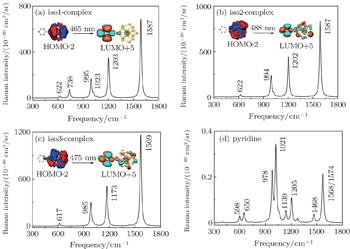 | Fig. 7. Charge-transfer resonance-enhanced Raman spectra, calculated at DFT level for three pyridine-Th@Au14 complexes at three different adsorption sites, corresponding to iso1 (a), iso2 (b), and iso3 (c) as indicated by the inset in Fig. |
For the two-dimensional P-complex and V-complex, the typical absorption peak of the P-complex is located at 370 nm (see Fig.
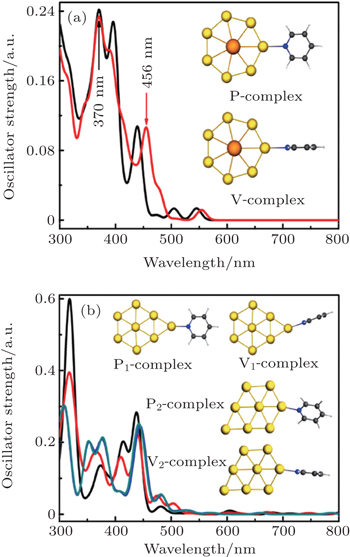 | Fig. 8. Absorption spectra and stable structures of (a) P-complex and V-complex, (b) P1-complex, V1-complex. P2-complex, and V2-complex, respectively. The subscripts 1 and 2 represent the different adsorption sites of Au8 structure. (Ac: orange, Au: luminous yellow, N: deep blue, C: deep grey, H: white). Adapted with permission from Ref. [7]. Copyright 2015 Royal Society of Chemistry. |
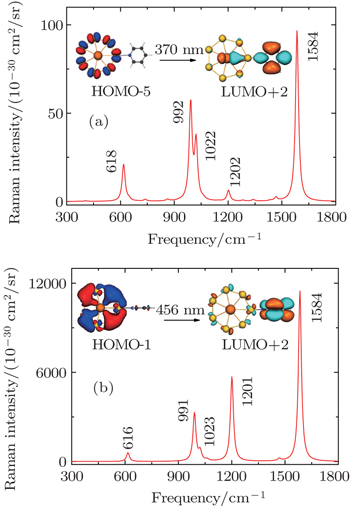 | Fig. 9. Calculated CT resonance-enhanced Raman spectra of (a) P-complex, (b) V-complex at the corresponding incident wavelength. Adapted with permission from Ref. [7]. Copyright 2015 Royal Society of Chemistry. |
In short, the optical absorption and SERS spectra of the 2D or 3D structures are strongly dependent on their electronic structures. Near the frontier MOs, each of these systems typically consists of a sparse set of superatomic orbitals, which arise primarily from the Au (6s) or actinide (5f, 6d or 7s) atomic orbitals. Furthermore, these superatomic orbitals can be split into several sets due to the limitation of symmetry. This splitting has an important effect on the optical absorption spectrum as multiple peaks result from transitions between superatomic orbitals. For the 2D or 3D complexes we studied, their electronic transitions are all from filled 1D superatom orbitals to virtual π bonding orbital of the pyridine ring. Also, all the maximum CT excitation bands are localized in the blue laser band, and commonly used in Raman spectrum measurement, especially the 488 nm, indicating SERS substrate materials containing actinide elements would have great advantages in adjusting excitation light.
We have designed a superatomic model series with different dimensions via first-principles DFT calculations. The 3D nanocage structures [An@Au14]n (where An = Ac, Th, Pa or U; n = −1, 0 or +1, respectively), all satisfy the 18-electron configuration of 1S21P61D10 jellium state that is analogous to the previously reported electronic structures such as W@Au12,[19] wherein the bonding involves primarily interactions between the s- and d-type shells of the endohedral atom and those of the gold-cage superatom (Au 6s orbitals). However, for the magnetic clusters (Pa@Au14 and U@Au14), these 5f-electron MOs maintain their original atomic orbital characteristics, and exhibit characteristics similar to those of the endohedral metallofullerenes (EMFs)[92–94] or passivated quantum dots.[95–100] The 2D planar structures, An@Au7 (An = La or Ac), each represent a closed-shell electronic structure with a 1S21P41D4 jellium model state, which is similar to previously reported structures, such as Ti@Au6, Sc@Cu7.[80,81] The 1D AcAu dimer structure is mainly formed by the combination of sigma and pi bonding orbitals. Next, a number of spectroscopic properties have been calculated and analyzed by TDDFT method. The results indicate that the allowed optical transitions involve mainly the superatomic orbitals. Furthermore, the CT-SERS spectra involve electronic transitions that are all from the filled 1D orbitals, which reveals the enhancement factors are of the order of ∼ 104 at 488 nm for 3D nanocage structures and of the order of ∼ 105 at 456 nm for 2D planar structures, respectively.
The above research results show that the superatom model formed from the coupling between 5f- and ds-electron can not only extend the wavelength range of electronic absorption spectra, but also bring a novel enhancement mechanism in the practical application, such as SERS spectra,[10,101] etc. So the superatom model containing 5f elements might improve the spectroscopic characteristics dramatically beyond previous implementations based on traditional atom models in the past. However, although the actinide-embedded superatom model has exhibited various advantages in theoretical simulations, the new field still faces multiple challenges including the modification of electronic structures the design of principle, and the condition of artificial synthesis, and so on.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 | |
| 92 | |
| 93 | |
| 94 | |
| 95 | |
| 96 | |
| 97 | |
| 98 | |
| 99 | |
| 100 | |
| 101 |