Aluminum-based intermetallic AlM₃ (M = Zr and Cu) binary alloys crystallize into the cubic Cu₃Au structure^[27,28] with space group Pm-3m (No. 221) consisting of Al atoms at the corners and M atoms at the face centers of the cube. The atomic positions are Al: 1a (0,0,0), and M: 3c (0,1/2,1/2). The ternary AlCu₂Zr alloy is a partially ordered Cu₂MnAl-type fcc (space group No. 225: Fm-3m) structure,^[29] where Al atoms occupy the 4a Wyckoff site (0,0,0), Cu atoms occupy the 8c site (1/4,1/4,1/4) and Zr atoms occupy the 4b site (1/2,1/2,1/2). In order to investigate the ground-state properties of AlM₃ (M = Zr and Cu) and AlCu₂Zr alloys, the geometry optimizations are performed first with the full relaxation of the cell shape and atomic positions. The equilibrium crystal structures of these compounds are shown in Fig. 1. The results of first-principles calculations of the structural properties of these compounds are presented in Table 1, together with the available experimental values^[27–29] and other theoretical results.^[10] The comparison shows that our results are in reasonable agreement with both theoretical and experimental values.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Crystal structures of AlM3 (M = Zr and Cu) and AlCu2Zr.

Table 1.

Table 1.

Table 1. Values of calculated and experimental lattice constant a (in unit Å), equilibrium volume V0 (in units Å3), bulk modulus B0 (in unit GPa) of AlZr3, AlCu3, and AlCu2Zr alloys. . Compounds a V0 B0 Ref. AlZr3 4.3799 84.02 99.2 this paper 4.381 84.11 100.8 [10] 4.392 84.70 – [27] AlCu3 3.6909 50.28 129.0 this paper 3.693 50.36 131.0 [10] 3.607 – – [28] AlCu2Zr 6.2525 244.43 129.4 this paper 6.256 244.81 128.6 [10] 6.216 240.21 – [29]

Table 1. Values of calculated and experimental lattice constant a (in unit Å), equilibrium volume V0 (in units Å3), bulk modulus B0 (in unit GPa) of AlZr3, AlCu3, and AlCu2Zr alloys. .

Generally, elastic constants of a solid permit us to obtain the mechanical properties and they can be used to describe the resistance of a crystal to an externally applied stress. They also provide important information about bonding characteristics near the equilibrium state. Thus, it is essential to investigate the elastic constants to understand the mechanical behavior of AlM₃ (M = Zr and Cu) and AlCu₂Zr compounds at equilibrium and under pressure. For a material with cubic symmetry, there are only three independent elastic constants, i.e., C₁₁, C₁₂, and C₄₄. In this paper, the calculated single crystal elastic constants of these compounds are listed in Table 2. It can be seen that the obtained elastic constants of the alloys agree well with the theoretical results in Ref. [10], which indicates that the DFT method we used in this study is reasonable. Furthermore, the corresponding requirements of mechanical stability in a cubic crystal lead to the following restriction on the elastic constants:^[30] C₁₁ +2C₁₂ > 0, C₄₄ > 0, C₁₁ −C₁₂ > 0. As shown in Table 2, all of the elastic constants for the compounds satisfy these criteria mentioned above, indicating that these compounds are mechanically stable.

Table 2.

Table 2.

Table 2. Values of calculated elastic constants Cij (in unit GPa), bulk modulus B (in unit GPa), shear modulus G (in unit GPa), Young’s modulus E (in unit GPa), Poisson’s ratio ν, elastic anisotropic factor A for AlZr3, AlCu3, and AlCu2Zr alloys at equilibrium. . Compound C11/GPa C12/GPa C44/GPa B/GPa G/GPa E/GPa B/G ν A Ref. AlZr3 147.4 75.2 74.2 99.2 55.6 140.5 1.78 0.264 1.52 this paper 148.7 79.4 70.8 102.5 53.4 136.5 1.92 0.278 1.49 [10] 163.8 79.3 86.5 107.7 – – – – – [5] AlCu3 152.4 117.3 85.4 129.0 45.9 123.1 2.81 0.341 1.89 this paper 150.7 120.6 81.9 130.6 43.6 117.7 3.00 0.350 1.89 [10] 176.0 117.4 92.4 136.9 49.6 132.8 – 0.340 – [4] AlCu2Zr 180.6 103.8 65.7 129.4 53.0 139.9 2.44 0.320 1.30 this paper 157.5 115.3 62.7 129.4 41.2 111.8 3.14 0.356 1.53 [10]

Table 2. Values of calculated elastic constants Cij (in unit GPa), bulk modulus B (in unit GPa), shear modulus G (in unit GPa), Young’s modulus E (in unit GPa), Poisson’s ratio ν, elastic anisotropic factor A for AlZr3, AlCu3, and AlCu2Zr alloys at equilibrium. .

The pressure dependences of the calculated elastic constants of AlZr₃, AlCu₃, and AlCu₂Zr are plotted in Fig. 2. The linear increases of elastic constants are due to the decreases of lattice parameters of all the compounds under pressure (not shown). It is noticeable that C₁₁ increases more rapidly with pressure than C₁₂ and C₄₄. C₁₁ represents elasticity in the x direction, i.e., in length, the longitudinal strain produces a significant change in volume. Again, the volume change is highly related to the pressure and thus produces a large change in C₁₁. Conversely, the constants C₁₂ and C₄₄ are related to the elasticity in shape.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Pressure dependences of elastic constants of (a) AlZr3, (b) AlCu3, and (c) AlCu2Zr.

The polycrystalline elastic properties, such as bulk modulus B, shear modulus G, Young’s modulus E, and Poisson’s ratio ν are estimated from the calculated single crystal elastic constants, and are presented in Table 2. The calculated results show that G for AlZr₃ is the largest, while for AlCu₂Zr it is less than that for AlCu₃, which agrees well with the available theoretical calculation.^[10]

The pressure effects on the calculated bulk modulus, shear modulus, and Young’s modulus of AlZr₃, AlCu₃, and AlCu₂Zr are shown in Fig. 3(a). The rate of increase of G with pressure is smaller than those of B and E. The shear modulus G is mainly due to the elastic constant C₄₄, because a large C₄₄ implies a stronger resistance to shear in the (100) plane. Young’s moduli of AlZr₃ and AlCu₂Zr are nearly equal at P = 0 GPa but when pressure increases the Young’s modulus for AlCu₂Zr increases more rapidly than those for the other two phases, which indicates that AlCu₂Zr phase is much stiffer than the other two phases at high pressure.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Pressure effects on (a) bulk modulus (B), shear modulus (G), and Young’s modulus (E); (b) the values of ratio of bulk modulus to shear modulus (B/G) and Poisson’s ratio (ν) of AlZr3, AlCu3, and AlCu2Zr.

Figure 3(b) shows the pressure dependences of Poisson’s ratio and B/G of AlZr₃, AlCu₃, and AlCu₂Zr. Poisson’s ratio can reflect the bonding properties of material. For the different bonding materials, Poisson’s ratios are different.^[31] As for a covalent material, the value of ν is small (typically ∼ 0.1); for an ionic material, the typical value of ν is 0.25; for a metallic material, ν is typically 0.33.^[31] In this case, Poisson’s ratio ranges from 0.264 to 0.341, which indicates that the AlM₃ (M = Zr and Cu) and AlCu₂Zr compounds show metallic behaviors. Poisson’s ratio increases with pressure increasing, the larger Poisson’s ratio signifies better plasticity. Hence it can be said that AlCu₃ possesses better plasticity than the other two phases. Additionally, in order to evaluate the ductility of material, a parameter B/G has been proposed by Pugh.^[32] The critical value separating ductility from brittleness is about 1.75. In the present work, the calculated values of B/G (Table 2) for these three compounds are all higher than 1.75, implying that AlM₃ (M = Zr and Cu) and AlCu₂Zr alloys behave in a ductile manner. Figure 3(b) shows that B/G increases with pressure growing for all the compounds under study. It indicates that AlZr₃, AlCu₃, and AlCu₂Zr are ductile compounds at up to 50 GPa. Anisotropy is used to describe situations where properties vary systematically, dependent on the direction. A = 2C₄₄/(C₁₁ − C₁₂) is called a shear anisotropy factor, often used to represent the elastic anisotropy of crystals.^[33] The A values of 1.52, 1.89, and 1.30 for AlM₃ (M = Zr and Cu) and AlCu₂Zr alloys, respectively quantify elastic anisotropies. It is noted that AlCu₃ phase is much more anisotropic than the other two phases.

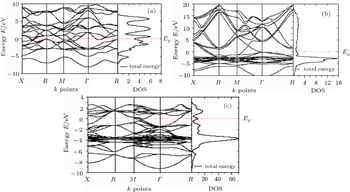
The investigated electronic band structures along high symmetry directions in the Brillouin zones together with the total densities of states (DOSs) of AlZr₃, AlCu₃, and AlCu₂Zr are depicted in Fig. 4. The band structures reveal metallic characters with dispersion bands crossing the Fermi level (E_F) for all structures. For AlZr₃ and AlCu₂Zr alloys, Zr 4d orbitals are mainly responsible for the metallic characters. But for AlCu₃, at the Fermi level, the main contribution comes from the Cu 3d orbitals.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Band structures and total DOSs of (a) AlZr3, (b) AlCu3, and (c) AlCu2Zr.

It is observed from Fig. 4(a) that for AlZr₃ alloy, the hybridization between Al 3p orbital and Zr 4d orbital is strong both below and above the Fermi level. For this reason the entire DOS can be divided into bonding and anti-bonding regions and therefore a pseudogap resides in between. The characteristic pseudogap around the Fermi level indicates the presence of the directional covalent bonding. The Fermi level located at a valley in the bonding region implies that the system has a pronounced stability.^[10] There is a general consideration that the formation of covalent bonding would enhance the strength of material in comparison with the pure metallic bonding.^[34]

According to the covalent approach, the guiding principle is to maximize bonding. Hence the stability increases with increasing occupancy in the bonding region, for a series of compounds having the same structure.^[35] Therefore it can be said that AlZr₃ is structurally more stable than AlCu₃. On the other hand, for AlCu₂Zr, the main bonding peaks from Fermi level to 3 eV predominantly derive from the Zr 4d orbitals. The phase stability of intermetallic compound depends on the location of the Fermi level and the value of the DOS at E_F.^[36,37] The lower value of DOS at E_F corresponds to a more stable structure. The values of the total DOS at the Fermi level in states are 3.2 eV and 9.3 eV for AlZr₃ and AlCu₂Zr alloys, respectively. Therefore, it can be said that AlZr₃ has a more stable structure than the other two alloys of Al under consideration, which agrees very well with the observation in Ref. [10].

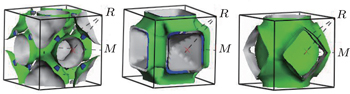
The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline lattice and from the occupation of electronic energy bands. It separates unfilled orbitals from the filled orbitals. The Fermi surface topologies of AlZr₃, AlCu₃, and AlCu₂Zr are shown in Fig. 5. The shapes of the Fermi surfaces are quite different for the three Al-based intermetallic compounds. In the cases of AlZr₃ and AlCu₃, two energy bands cross the Fermi level. They form two Fermi sheets. AlZr₃ has a hole-like Fermi surface around R point as well as around X point. The topology of the Fermi surface of AlZr₃ is nearly similar to that of YPb₃.^[38] Again, AlCu₃ has two hole-like Fermi sheets around X point. On the other hand, AlCu₂Zr alloy has four Fermi sheets because four energy bands cross the Fermi level. The topology of this Fermi surface is complicated; it has hole-like sheets around R point and electron-like sheets around Γ point.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Fermi surfaces of (a) AlZr3, (b) AlCu3, and (c) AlCu2Zr.

Charge transport is mainly limited by carrier–carrier and carrier–phonon scattering. Besides, there is always impurity scattering in most real systems. The carrier–carrier scattering is intimately related to the electronic band structure and density of states at the Fermi level. The topology of the Fermi surface also plays a role. For example, the highly dispersive nature of energy dispersion curve for AlZr₃ (Fig. 4(a)) around the Fermi energy, implies high carrier mobility. This is supported by the large low energy optical conductivity seen in Fig. 11(h) for the same compound (AlZr₃).

The thermodynamic properties such as the bulk moduli, specific heats, Debye temperatures, and volume thermal expansion coefficients at different temperatures and pressures are evaluated for the first time for these compounds. We calculate all the thermodynamic properties in a temperature range from 0 K to 1000 K and a pressure range from 0 GPa to 50 GPa, where the quasi-harmonic Debye model remains valid.

In the quasi-harmonic model, the nonequilibrium Gibbs function G∗(V;P,T) can be written as^[22]

The temperature dependences of adiabatic bulk modulus, B of AlZr₃, AlCu₃, and AlCu₂Zr alloys at P = 0 GPa are shown in Fig. 6(a). Our calculations exhibit that B value for AlCu₂Zr is nearly flat whereas for AlZr₃ compound, it decreases with temperature increasing up to 1000 K. We also note that in a temperature range of 0 K–600 K, B fluctuates for AlCu₃, it then decreases smoothly with temperature increasing until 1000 K. For AlZr₃, AlCu₃, and AlCu₂Zr alloys, the values of B are found respectively to be 99 GPa, 126 GPa, and 129 GPa at P = 0 GPa and T = 0 K, which are in good agreement with the values computed using elastic constant data (Table 2).

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Temperature dependences of (a) adiabatic bulk modulus and (b) Debye temperature of AlZr3, AlCu3, and AlCu2Zr.

Debye temperature is basically a measure of the vibrational response of the material. Debye temperature is not a strictly determined parameter; various estimates may be obtained through well-established empirical or semi-empirical formula, relating Θ_D to various macroscopic properties.^[39] Figure 6(b) depicts the temperature dependences of Debye temperature, Θ_D of AlZr₃, AlCu₃, and AlCu₂Zr compounds at zero pressure. Our calculated values of Θ_D using the quasi-harmonic Debye model are 367 K, 377 K, and 476 K, respectively for AlZr₃, AlCu₃, and AlCu₂Zr alloys at zero pressure and zero temperature, which are in reasonable agreement with the values of 385 K, 381 K, and 397 K estimated using elastic constants data. These may be compared with the calculated value of Θ_D for Ni₃Al is 466 K.^[12]

It is observed from Fig. 6(b) that Θ_D is the highest for AlCu₂Zr and the lowest for AlZr₃ at zero temperature and pressure. The Debye temperatures decrease slowly with increasing temperature for AlCu₂Zr and AlZr₃. But for AlCu₃, the Debye temperature decreases faster than those of the other two compounds. The temperature variations of all the phases reveal that there is a strong bonding in both the AlCu₂Zr and AlZr₃ compounds where a weak bonding occurs in AlCu₃, which coincides with the DOS and elastic properties. This is due to the fact that the Debye temperature is related to the volume, V and adiabatic bulk modulus, B. The adiabatic bulk modulus B decreases and increases with increasing temperature and pressure, respectively but the volume, V, behaves in an opposite manner. It is found in Ref. [22] that B makes more contribution to the Debye temperature than, V. On the other hand, Debye temperature increases with increasing pressure (not shown).

The specific heat of the material is usually approximated by the contribution of the lattice specific heat. Figure 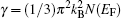7 presents the estimated results on the temperature dependences of constant-pressure and constant-volume specific heat capacities C_P, C_V of AlZr₃, AlCu₃, and AlCu₂Zr alloys. Due to the increase of temperature, phonon thermal softening occurs and hence heat capacities increase. The differences between C_P and C_V for AlZr₃, AlCu₃, and AlCu₂Zr alloys are due to the thermal expansion caused by anharmonicity effects.^[40] In the low temperature limit, the specific heat exhibits the Debye T³ power-law behavior; at high temperature (T > 300 K), the anharmonic effect on heat capacity is suppressed, and C_V approaches the classical asymptotic limit C_V = 3nNk_B = 99.7 J/mol·K. These results exhibit the fact that the interactions between ions in AlZr₃, AlCu₃, and AlCu₂Zr alloys have large effects on heat capacities especially at low temperatures. The calculations of Fatmi et al.^[12] for a similar type of compound coincide with our results. To evaluate the electronic contribution to specific heat through the Sommerfeld constant, γ within the free electron model: , we can use N(E_F) from the investigated DOS for the three alloys. This scheme gives the values 7.55, 2.95, and 21.93 mJ·mol⁻¹·K⁻² for AlZr₃, AlCu₃, and AlCu₂Zr alloys, respectively.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Specific heats at constant (a) pressure and (b) volume versus temperature of AlZr3, AlCu3, and AlCu2Zr.

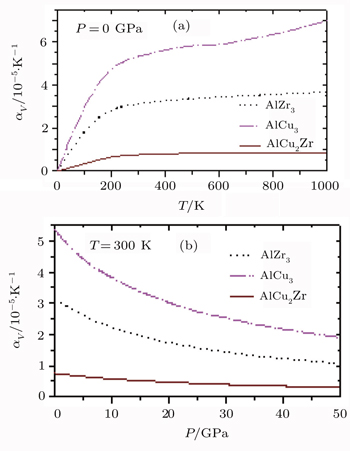
Finally, the computed results on the variations of the volume thermal expansion coefficient, α_v with temperature and pressure for AlZr₃, AlCu₃, and AlCu₂Zr alloys are displayed in Fig. 8. The volume thermal expansion coefficient, α_v reflects the temperature dependence of volume at constant pressure: α = (1/V)(dV/dT)_P. Figure 8(a) depicts the temperature dependence of α_v at P = 0 GPa. The coefficient, α_v increases rapidly as the temperature increases up to ∼ 300 K and then gradually approaches towards a linear increase with temperature rising and the propensity of increment becomes moderate, which means that the temperature dependence of α_v is very small at high temperature. For a given temperature, the coefficient decreases drastically with the increase of pressure. The pressure dependence of α_v at 300 K is presented in Fig. 8(b). At high temperatures and high pressures, the thermal expansion would converge to a constant value. With temperature rising, the average amplitude of atomic vibrations increases. For an anharmonic potential, it corresponds to the increase in the average value of inter-atomic separation, i.e., thermal expansion. The stronger the inter-atomic bonding, the smaller the thermal expansion is. The values of α_v are found to be 7.5×10⁻⁶ K⁻¹, 3.1×10⁻⁵ K⁻¹, and 5.3×10⁻⁵ K⁻¹ for AlCu₂Zr, AlZr₃, and AlCu₃ alloys, respectively at P = 0 GPa and T = 300 K. The higher value of AlCu₃ indicates that it is softer than the other two compounds. For a given temperature, the coefficient α_v sharply decreases with the increase of pressure but for AlCu₂Zr, it is almost constant (see Fig. 8(b)). To date, there have been no experimental results nor other theoretical investigations for the thermal properties of AlZr₃, AlCu₃, and AlCu₂Zr alloys; our investigations may serve as a guide for future research.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Variations of αv with (a) temperature and (b) pressure of AlZr3, AlCu3, and AlCu2Zr.

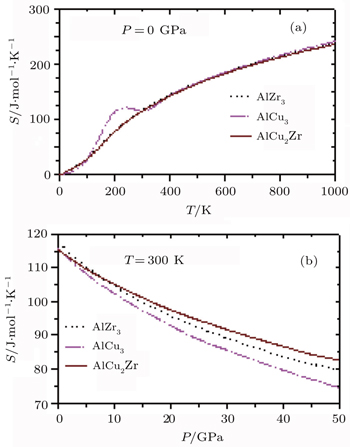
The variations of entropy, S of AlZr₃, AlCu₃, and AlCu₂Zr alloys each as a function of temperature and pressure are shown in Fig. 9. It is observed from Fig. 9(a) that at P = 0 GPa, S increases with increasing temperature. The rates of increase of entropy with temperature are almost the same for the compounds under study. This type of diagram is used in thermodynamics because it helps to visualize the heat transfer in the process. Entropy is a measure of how much the energies of atoms and molecules become more spread out in a process. Figure 9(b) shows that the entropy decreases with increasing pressure. This is due to the fact that when the pressure on the system increases, the volume decreases. The energies of the particles are in a smaller space, so they are less spread out. Hence the entropy decreases. It is observed from Fig. 9(b) that the rate of decrease of S is the largest for AlCu₃ and the smallest for AlCu₂Zr. Therefore the volume of AlCu₃ is more compressible than those of the other two Al-based alloys under the same pressure.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Variations of S with (a) temperature and (b) pressure for AlZr3, AlCu3, and AlCu2Zr.

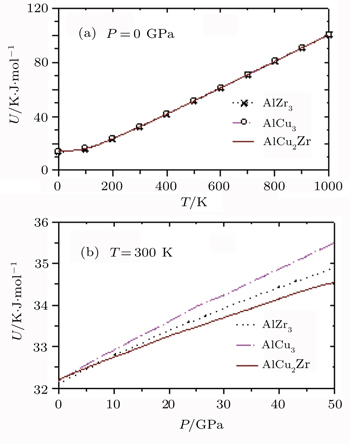
The temperature and pressure variations of the calculated internal energies for AlZr₃, AlCu₃, and AlCu₂Zr alloys are shown in Fig. 10. The internal energy is the energy associated with the random, disordered motions of molecules. It is observed from Figs. 10(a) and 10(b) that the internal energies increase with temperature and pressure increasing. At P = 0 GPa the rates of increase of U with temperature increasing are the same for all the compounds under study. On the other hand, at room temperature (T = 300 K), the internal energies increase 5.62%, 6.68%, and 4.72% for AlZr₃, AlCu₃, and AlCu₂Zr alloys respectively, when the pressure changes from 0 GPa to 50 GPa.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. (a) Temperature and (b) pressure dependences of U for AlZr3, AlCu3, and AlCu2Zr.

The optical properties of AlZr₃, AlCu₃, and AlCu₂Zr alloys may be derived from the knowledge of the complex dielectric function, ɛ(ω). Generally, there are two contributions for ɛ(ω), namely from intraband and interband transitions. The contribution from the latter is vital only for metals.^[41] The complex dielectric function can be expressed as ɛ(ω) = ɛ₁(ω)+ iɛ₂(ω). The imaginary part ɛ₂(ω) is obtained from the momentum matrix elements between the occupied and unoccupied wave functions within the selection rules, whereas the real part ɛ₁(ω) of dielectric function can be derived from the imaginary part using the Kramers–Kronig relation. The knowledge of both ɛ₁(ω) and ɛ₂(ω) allows the calculation of important optical constants such as the refractive index n(ω), extinction coefficient k(ω), conductivity, optical reflectivity R(ω), absorption coefficient α(ω), and energy-loss spectrum L(ω) using the expressions given in Ref. [42]. The calculational approaches are well established and widely available in the literature^[43,44] and hence will not be repeated here.

The estimated optical properties of AlZr₃, AlCu₃, and AlCu₂Zr alloys at ground state are presented in Fig. 11, for the photon energy ranging from 0 eV up to 20 eV for polarization vector [100]. The available theoretical data for Ni₃Al^[12] are also shown in the plots for comparison. Dielectric function is the most general property of a solid, which modifies the incident electromagnetic wave of light. Figures 11(a) and 11(b) show the real and imaginary parts of the dielectric function for AlZr₃, AlCu₃, and AlCu₂Zr alloys along with the calculated values of Ni₃Al. Our results are similar to those for Ni₃Al.^[12] The electronic band structure analysis shows that AlZr₃, AlCu₃, and AlCu₂Zr alloys are metallic. Therefore, Drude term correction is required to include the effect of metallicity.^[45,46]

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. (a) Real and (b) imaginary parts of dielectric function, (c) real and (d) imaginary parts of refractive index, (e) absorption, (f) loss function, (g) reflectivity, and (h) real part of conductivity of AlZr3, AlCu3, and AlCu2Zr.

The plasma frequencies of 10 eV, 4 eV, 6 eV, and damping values of 0.07 eV, 0.05 eV, 0.02 eV are used for AlZr₃, AlCu₃, and AlCu₂Zr alloys, respectively. For all calculations, we use a 0.5-eV Gaussian smearing. The real part ɛ₁ goes through zero from below about 14.52 eV, 21.66 eV, 12.47 eV and the imaginary part ɛ₂ approaches zero damping values of 14.98 eV, 22.80 eV, and 12.98 eV for AlZr₃, AlCu₃, and AlCu₂Zr alloys, respectively. Metallic reflectance characteristics are exhibited in the range ɛ₁ < 0.

The velocity of propagation of an electromagnetic wave through a solid is given by the frequency dependent complex refractive index N = n + ik, where the real part n is related to the velocity and the imaginary part k, the extinction coefficient is related to the decay or damping of the oscillation amplitude of the incident electric field. The refractive indexes and extinction coefficients are illustrated in Figs. 11(c) and 11(d). The static refractive index n(0) is found to have the values 11.8 (AlCu₃), 19.3 (AlZr₃), and 12.4 (AlCu₂Zr), which agrees well with that of another Al-based intermetallic compound Ni₃Al (14.56).^[12] The values of extinction coefficients, k each show a maximum value at 0.0 eV, then they decrease rapidly and turn to zero at about 15.0 eV, 22.96 eV, and 12.43 eV for AlZr₃, AlCu₃, and AlCu₂Zr alloys, respectively.

Figure 11(e) shows the absorption coefficient spectra of the AlZr₃, AlCu₃, and AlCu₂Zr alloys, which begin at zero photon energy due to their metallic nature. In Fig. 11(e), we show the absorption coefficient spectrum with one peak between 0.78 eV and 5.73 eV for AlZr₃ which rises and then decreases rapidly in the high-energy region. Nearly the same features can be seen for AlCu₃ and AlCu₂Zr but with two prominent peaks for AlCu₃. The highest peaks appear at 7.55 eV, 6.26 eV, and 5.80 eV for AlZr₃, AlCu₃, and AlCu₂Zr alloys, respectively. The absorption coefficient spectrum of Ni₃Al is also shown in Fig. 11(e) for comparison, for which the highest peak occurs at 14.93 eV.^[12] It is observed from the figure that at higher photon energies, Ni₃Al and AlCu₃ have roughly similar absorption coefficient spectra.

Loss function is intimately related to absorption and reflection. Loss function refers to the fast electron traversing in a material. It is clear from the study of the figure that maximum reflectivity occurs where the minimum absorption takes place. So the study of loss function is the most important in material study. The electron energy loss function L(ω) is depicted in Fig. 11(f). The peaks in L(ω) spectra represent the characteristics associated with the plasma resonance and the corresponding frequency is the so-called plasma frequency, ω_P,^[47] which occurs at ɛ₂ < 1 and ɛ₁ = 0.^[46,48] The peaks of L(ω) located at 14.5 eV, 21.7 eV, and 12.4 eV correspond to plasma frequencies of AlZr₃, AlCu₃, and AlCu₂Zr alloys, respectively. Further, these peaks correspond to irregular edges in the reflectivity spectra (Fig. 11(g)), and hence an abrupt reduction occurs at each of these peak values in the reflectivity spectra. If the incident light has frequency greater than the plasma frequencies of the alloys under study, these alloys will be transparent and will change from metallic to dielectric response.

The variations of calculated optical reflectivity R(ω) with incident photon energy are displayed in Fig. 11(g). It is observed from the figure that AlZr₃ and AlCu₂Zr have their maximum reflectivity values (∼100%) in the infra-red region as well as in the ultra-violet region. On the other hand, AlCu₃ has maximum reflectivity only in the infra-red region. Again in the visible light region (energy range ∼1.8 eV–3.1 eV), it is observed from Fig. 11(g) that AlCu₃ has larger reflectivity than those of the AlZr₃ and AlCu₂Zr alloys, but all of them have reflectivities more than 44%. This indicates that the capability of AlCu₃ to reflect visible light is stronger than those of the other two alloys. On the other hand, AlZr₃ and AlCu₂Zr alloys are better reflectors than that of the AlCu₃ alloy in the ultra-violet region. According to Li et al.,^[45] a MAX-phase compound will be capable of reducing solar heating if it has a reflectivity of ∼ 44% in the visible light region. Hence, we may conclude that all the compounds under study are also candidate materials for coating to reduce solar heating.

For the three alloys, their photoconductivities start with zero photon energy (Fig. 11(h)). This indicates that the materials have no band gap that is evident from band structure calculations (Fig. 2). Moreover, the photoconductivities and hence electrical conductivities of these materials increase as a result of absorbing photons. From Fig. 11(h), we observe that the maximum optical conductivities occur at energy 2.72 eV for AlZr₃, 5.40 eV for AlCu₃, and 3.21 eV for AlCu₂Zr within the energy range of 2 eV to 6.84 eV, respectively. This implies that AlCu₃ will be more highly electrically conductive than the other two alloys when the incident radiation has an energy within this range. The photoconductivities reach zero at about 10 eV for both the compounds AlZr₃ and AlCu₂Zr; AlCu₃ also reaches zero but at 22.5 eV (not shown). There is a photoconductivity for none of the phases when the photon energy is higher than 22.5 eV. We are not aware of any other theoretical calculations or experimental data for the optical properties of AlZr₃, AlCu₃, and AlCu₂Zr alloys. Thus, our results would provide a useful reference for further investigations.