† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11175160, 11275075, and 11575160).
Based on statistical properties, two typical models are considered to calculate the uncertainties for some random noise sequences on the period extraction of a torsion pendulum, which is important and instructive in the measurement of gravitational constant G with the time-of-swing method. An expression of the uncertainty for the period measurement is obtained, which is dependent on the ratio Δt/(1/λ) where Δt is the interval of the sample time and 1/λ is the length of the correlation time. The result of processing experimental data shows that as the interval of the sample time Δt gradually shortens, the uncertainty of the period becomes smaller, and further when the ratio Δt/(1/λ) is less than 1, the uncertainty remains substantially unchanged.
The period determination of a torsion pendulum with high precision is of great importance for some gravitational experiments.[1–3] For example, in the measurement of the Newtonian gravitational constant G with the time-of-swing method, one needs to determine the periods of the torsion pendulum at different configurations of source masses with high precision.[4–10] The measurement accuracy of G is directly restricted by the period extraction accuracy.
The torsion pendulum is one of the most sensitive physical measurement devices, and has been recognized and applied widely over the last two centuries since Cavendish’s measurement of the gravitational constant G.[11] As a highly sensitive device, the sensitivity and precision of the torsion pendulum are inevitably limited by a variety of noises, and thus the precision of period estimation is also limited by these noises. Based on statistical properties, some random noise sequences obey the Gaussian probability density distribution and have definite correlation time,[12,13] which could be generally divided into two categories. One is named the Gaussian white noise, which is a statistically independent random variable. In fact, the random noise sequence of which the correlation time length is far smaller than the sampling interval could be viewed as the Gaussian white noise. Maybe the Gaussian white noise is not a perfect model for torsion balance experiment, but it is useful and advisable for theoretical analysis to judge whether a method is good or not.[14] The other is defined as the Gaussian colored noise, whose correlation time length is larger than the sampling interval. For example, the random noise resulting from the angle-deflection readout system in the experiment should be viewed as the Gaussian colored noise.[15] Obviously, the effect of the Gaussian colored noise on the period extraction of the pendulum is well worth studying.
The influences of many noises on the period extraction of a torsion pendulum have been studied in detail before.[14–19] These relevant studies focused on the effects caused by specific noises of different origins and corresponding contributions of these noises to the uncertainty of period extraction. Besides, with the correlation time obtained, the use of the noise model and the setting of a suitable interval of the sample time are significant issues which need solving. In this condition, it is necessary to analyze the relation of the uncertainty of the pendulum period with the correlation time and the interval of the sample time.
In this paper, two typical noise models are considered to analyze the influence of the random noise sequence on the period extraction of a torsion pendulum. Though there are a variety of methods to determine the period of the pendulum,[1,14,15,17,20] the correlation method, which is used in our analysis, is one of the most efficient and accurate methods for subtle signal processing since it is insensitive to higher order harmonics, nor the damping effect nor the slow drift of the period.[14] The uncertainty expression of the Gaussian colored noise on the period extraction is derived in detail and compared with that of the Gaussian white noise. According to the formula of the uncertainty, we can conclude that the uncertainty expressions of the Gaussian white and colored noises are dependent on the sampling interval and length of the correlation time respectively. Generally, with the interval of sample time far smaller than the length of the correlation time, the Gaussian colored noise model is used to analyze the random noise sequence, and otherwise the Gaussian white noise model is used. Meanwhile, if the length of the correlation time of a random noise sequence is known, the interval of the sample time can be determined directly according to the requirement for the period accuracy. Consequently, the applicable noise model could be chosen to obtain the uncertainty correspondingly. Finally, an analysis of typical experimental data of the measurement of G with the time-of-swing method further shows that as the interval of the sample time gradually shortens, the uncertainty of the period becomes smaller consequently, and when the ratio between the sampling interval and the correlation time is less than 1, the uncertainties remain substantially unchanged.
Due to the sensitivity of measurement device and change of external experiment environment, the actual period of torsion pendulum is inevitably influenced by varieties of noises. Based on statistical properties, the Gaussian white noise model is usually used to analyze the influences of some random noise sequences.[14,19,21] In fact, there may be no strict white noise in the nature environment, and many noises have a definite correlation time each. Generally, when the correlation time of noise is far less than the relevant time of the system, the Gaussian white noise model is used to deal with the noise.[22] However, there are many noises with a relatively long correlation time in the experimental environment. On this condition, the Gaussian white noise model cannot be used any more, and hence it is necessary to use the Gaussian colored noise model to analyze the influence of this kind of noise.
The Gaussian colored noise is one of the most popular and applicable colored noise models. Although the physical origin of this kind of noise is as yet unknown, which usually has a definite correlation time and complies with Gaussian distribution. The expectation value and correlation function of the noise ɛic are expressed, respectively, as[12,13]
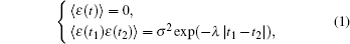
In experiment, the experimental signal yi of torsion pendulum is expressed as


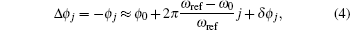
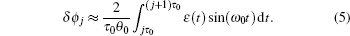

By performing the linear fitting of the phase difference sequence {Δϕj} and number sequence {j}, the frequency ω can be estimated from





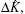



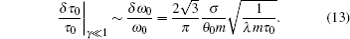
Unlike the Gaussian colored noise, the Gaussian white noise is a kind of ideal mathematical model. In fact, the random noise sequence, of which the correlation time length is far smaller than the sampling interval, could be modeled as the Gaussian white noise. For example, the environmental noise and the thermal noise caused by the Brown motion can be viewed as the white noise model.[15,19] The expectation value and correlation function can be given, respectively, as[14]

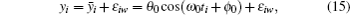

Similarly, the standard deviation is used to calculate the error of the slope, and expressed as
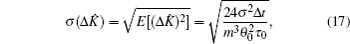
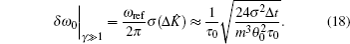

According to Eqs. (

 | Fig. 1. Relationship between the normalized uncertainty and the interval of the sample time. f(γ) is the normalized uncertainty of the period, γ = Δt/(2/λ) represents the different interval of the sample time on the condition that the length of the correlation time is set as a constant. Each point denotes the normalized statistical uncertainty. The solid line is obtained by the polynomial fitting between simulated uncertainties and the different ratio γ. Some points in the plot are covered by the solid line. Referring to the real experimental data in the experiment of measuring G with the time-of-swing method,[23] the simulation parameters are set respectively. |
It is obvious that the simulation results are in good agreement with the theoretical uncertainty in Eq. (
In the experiment of measuring G with the time-of-swing method,[23] each data set is taken in a regular total sample time of about 3 days in intervals of 0.5 s (i.e., the sample time Δt = 0.5 s). The total sample time cannot be too long because of the damping effect of torsion pendulum and the influence of external experimental environment. Figure
In this work, the influences of the Gaussian white and colored noises on the period determination of a torsion pendulum are discussed respectively. According to the correlation method, the uncertainties of random noise sequences on the period extraction are formalized. Corresponding numerical simulations indicate that for a random noise sequence, with the correlation time length known, according to the requirement for the period extraction accuracy, the suitable interval of the sample time can be determined directly, and thus the applicable noise model is chosen to obtain the uncertainty correspondingly. If the interval of the sample time Δt ≪ (1/λ), the random noise sequences should be modeled as a Gaussian colored noise, and if Δt ≫ (1/λ), the random noise sequences should be modeled as a Gaussian white noise. An experimental data analysis for the measurement of G with the time-of-swing method further shows that as the sample time gradually shortens, the uncertainty of the period becomes smaller consequently, and further when the ratio is less than 1, the uncertainty remains substantially unchanged. Though some of the above conclusions are based on numerical simulation and mathematical analysis, it is instructive for the improvement of the period extraction accuracy and the optimization of data acquisition system. Since many kinds of noises have not been fully understood so far, there is still much work to do in this field.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 |





