Cite this Article
Liu Zhi-Hao, Chen Han-Wu. Cryptanalysis and improvement of quantum broadcast communication and authentication protocol with a quantum one-time pad. Chinese Physics B, 2016, 25(8): 080308  
Permissions
Cryptanalysis and improvement of quantum broadcast communication and authentication protocol with a quantum one-time pad
Liu Zhi-Hao1, 2, 3, †, , Chen Han-Wu1, 2, ‡,
School of Computer Science and Engineering, Southeast University, Nanjing 211189, China
Key Laboratory of Computer Network and Information Integration (Southeast University), Ministry of Education, Nanjing 211189, China
Center for Quantum Computation and Intelligent Systems, Faculty of Engineering and Information Technology, University of Technology Sydney, NSW 2007, Australia

 

† Corresponding author. E-mail: lzh@seu.edu.cn

‡ Corresponding author. E-mail: hw_chen@seu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61502101 and 61170321), the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20140651), the Research Fund for the Doctoral Program of Higher Education, China (Grant No. 20110092110024), and the Project Funded by PAPD and CICAEET.

Abstract
Abstract

The security of quantum broadcast communication (QBC) and authentication protocol based on Greenberger–Horne–Zeilinger (GHZ) state and quantum one-time pad is analyzed. It is shown that there are some security issues in this protocol. Firstly, an external eavesdropper can take the intercept–measure–resend attack strategy to eavesdrop on 0.369 bit of every bit of the identity string of each receiver without being detected. Meanwhile, 0.524 bit of every bit of the secret message can be eavesdropped on without being detected. Secondly, an inner receiver can take the intercept–measure–resend attack strategy to eavesdrop on half of the identity string of the other’s definitely without being checked. In addition, an alternative attack called the CNOT-operation attack is discussed. As for the multi-party QBC protocol, the attack efficiency increases with the increase of the number of users. Finally, the QBC protocol is improved to a secure one.

PACS: 03.67.Dd;03.67.Hk;03.67.–a;03.65.Ud
Keyword:cryptanalysis;quantum broadcast communication;information leakage;intercept–measure–resend attack;CNOT-operation attack
1. Introduction

As one of the most developed branches of quantum cryptography, quantum key distribution (QKD) discusses the problem of how to distribute a secret key between two remote users with the quantum manner. The pioneers Bennett and Brassard[1] designed the first QKD protocol in 1984, where four nonorthogonal single-photon states were used. Afterward, Ekert[2] put forward another novel QKD protocol by using Einstein–Podolsky–Rosen (EPR) pairs in 1991, in which Bell inequality was for the first time used to evaluate the security of the quantum channel. In the next year, Bennett et al.[3] proposed a new QKD protocol based on two nonorthogonal single-photon states with unconditional security. After that, QKD[4–11] received much attention and fruitful achievement in both theoretical and experimental aspects. In recent years, another branch of quantum cryptography called quantum direct communication (QDC) was put forward. Different from QKD, QDC allows the sender to transmit directly the secret or the deterministic key (instead of a random key) to the receiver in a deterministic and secure manner. Compared with that in QKD, the security demands in QDC are more rigorous because the information transmitted is the meaningful secret instead of a random key, which cannot be eavesdropped. This means the information cannot be leaked out whether the eavesdropper would be discovered or not in QDC. In general, QDC can be divided into two categories: quantum secure direct communication (QSDC)[12–26] and deterministic secure quantum communication (DSQC).[27–35] The difference between QSDC and DSQC is that there are some classical bits communicated to assist the receiver to decrypt the secret in DSQC, while in QSDC there is not. Quantum broadcast communication (QBC)[36–38] as a special kind of QDC was put forward several years ago, which involves a sender and multiple receivers. For QBC, a sender broadcasts a secret message to a set of receivers with the quantum manner, and every receiver can get the same message.

Recently, Chang et al.[39] put forward a novel QBC and authentication protocol with a quantum one-time pad based on the Greenberger–Horne–Zeilinger (GHZ) state. For the sake of convenience, we refer to this QBC protocol as the QBC-CXZY protocol later. It was shown that one bit of information could be broadcasted from the sender to the receivers at the cost of a GHZ state consumed. The classical exclusive-or (XOR) operation serving as a one-time-pad was used to forbid the eavesdroppers to eavesdrop on the secret transmitted by the sender. Eavesdropping detection and identity authentication were implemented at the same time based on previously shared identity strings. It was claimed that the identity strings could be reused with unconditional security and no hash function or local unitary operation was used. However, if considering this protocol carefully, one can find that it in fact has some security issues. An eavesdropper can take the intercept–measure–resend attack strategy to eavesdrop on some information of the identity strings of the receivers and the secret message without being detected. Moreover, one receiver can take the intercept–measure–resend attack more efficiently than the external eavesdropper to eavesdrop on the other’s identity string without being detected. As for the multi-party QBC-CXZY protocol, the attack efficiency increases with the increase of the number of users. In the following context, we will cryptanalyze the QBC-CXZY protocol from the viewpoint of information theory.

2. Description of the QBC-CXZY protocol

Suppose that the sender Alice wants to broadcast her secret message to two receivers Bob and Charlie. Bob and Charlie have the secret N-bit strings IDB and IDC representing their identities respectively. Alice shares IDB and IDC with Bob and Charlie respectively. The QBC-CXZY protocol consists of the following steps.

Step 1 Alice prepares N ordered three-particle GHZ states to transmit the secret message. Each of them is in the state

Then, Alice takes particles 1, 2, and 3 from each state to construct three ordered sequences S1, S2, and S3, which are expressed as the following forms: {P1(1),P2 (1),…,PN (1)}, {P1 (2),P2 (2),…,PN (2)}, and {P1 (3),P2 (3),…,PN (3)} respectively.

Step 2 According to IDB and IDC, Alice prepares two N-qubit sequences SIDB and SIDC. The rule is that she randomly prepares the i-th qubit of SIDB (SIDC) in one of the two states in Z-basis {|0〉,|1〉} if the i-th bit of IDB (IDC) is 0; otherwise, she randomly prepares the qubit in one of the two states in the X-basis

Step 3 According to IDB and IDC, Alice mixes SIDB and SIDC to S2 and S3 to form S′2 and S′3 respectively. The rule is that if the i-th bit of IDB is 0, Alice puts the i-th particle of SIDB behind the i-th particle in S2; otherwise, she puts the i-th particle of SIDB before the i-th particle in S2. In the same way, SIDC is mixed into S3 to form S′3. After that, Alice transmits S′2 and S′3 to Bob and Charlie respectively.

Step 4 After Bob and Charlie receive S′2 and S′3, they extract SIDB and SIDC according to IDB and IDC, and then measure the particles in each sequence using the right bases respectively.

Step 5 According to the respective measurement results of SIDB and SIDC, Bob and Charlie generate the classical bit sequences DB and DC respectively. That is, states |0〉 and |+〉 both represent classical bit 0, and states |1〉 and |−〉 represent classical bit 1. After that, Bob and Charlie publicly announce DB and DC respectively. Then, Alice compares Bob’s and Charlie’s results with the initial states of SIDB and SIDC respectively. If the error rates are low enough, Alice believes that Bob and Charlie are legal and no eavesdropping exists, and thus the communication goes on. Otherwise Alice interrupts it.

Step 6 Bob and Charlie respectively measure particles in S2 and S3 with Z-basis in order to get the ordered classical bit sequences CS2 and CS3 with the rule that the states |0〉 and |1〉 correspond to classical bits 0 and 1 respectively.

Step 7 Alice measures the particles in S1 in order with Z-basis and constructs the ordered classical string CS1. Assume that the secret message Alice wants to send is M, then Alice encrypts it with CS1 bit-by-bit by exclusive-or (XOR) operation to get C (C = M ⊕ CS1). After that, Alice publishes C.

Step 8 According to CS2 and CS3, Bob and Charlie decrypt C to get the secret message M by XOR operation. That is, M = C ⊕ CS2 = C ⊕ CS3.

Step 9 Two receivers Bob and Charlie store and deal with the secret message M.

Step 10 Alice, Bob and Charlie continue to the second transmission.

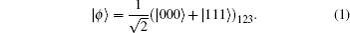
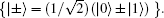
In the QBC-CXZY protocol, there are some obvious features. Firstly, the security of the protocol completely depends on the security of the identities, because eavesdropping check and identity authentication are implemented at the same time. Secondly, only Z-basis measurement is used to decrypt the secret message, so if an eavesdropper (Eve) happens to make a Z-basis measurement on a transmitted particle which comes from a GHZ state, there is no error introduced.

3. Cryptanalysis of the QBC-CXZY protocol
3.1. An external eavesdropper eavesdropping on the identity strings of the receivers and the secret message

Now we consider the situation that an external eavesdropper (Eve) eavesdrops on some information of the identity strings of the receivers (IDB and IDC) and the secret message without bringing any error. The attack strategy is described as follows.

Rule 1 If a couple of the corresponding bits from DB and E2 are different, she can immediately deduce that she has measured a particle from S2, which means IDB = 1. This is because if IDB = 0, then she has measured a particle from SIDB according to the rule that SIDB is mixed into S2 in the Step 3 of the QBC-CXZY protocol, and thus DB must be identical to E2. Similarly, if a couple of the corresponding bits from DC and E3 are different, Eve can immediately deduce that she has measured a particle from S3, which means IDC = 1;

Rule 2 If Eve has deduced that some bit of IDB (IDC) is 1, she can immediately infer that the corresponding bit of CS2 is equal to that of E2 (the corresponding bit of CS3 is equal to that of E3). This is because if some bit of IDB (IDC) is 1, Eve knows the particle she has measured is from S2 (S3) but this does not bring any error. That is to say, Eve gets CS2 (CS3) in this situation;

Rule 3 If Eve has inferred some bit of IDB(IDC) is equal to 1, but the corresponding bits of CS2 (CS3) and E3(E2) are not equal, then Eve can deduce that the corresponding bit of IDC(IDB) is equal to 0 according to the rule that SIDC (SIDB) is mixed into S3 (S2) in Step 3 of the QBC-CXZY protocol;

Rule 4 In other cases, Eve cannot infer the direct values of IDB, IDC, and CS2 (CS3), but this does not mean they are useless from the viewpoint of information theory because the posterior probability distributions of the bits of IDB, IDC, and CS2 (CS3) may be changed.

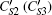
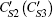
To understand the above rules more unambiguously, we can refer to Table 1. Now we will take the 10th row of Table 1 as an example to explain how Eve can deduce where represents the classical bit string about CS2 (CS3) that Eve can deduce. Because DC ≠ E3, Eve can deduce IDC is equal to 1 (Rule 1). Thus Eve knows that she has measured the particle from S3 without bringing any error. This means (Rule 2). As a result, Eve can deduce the corresponding bit of the secret by M = C ⊕ C′S2 = C ⊕ C′S3.

Table 1.

Using DB, DC, E2, and E3 to deduce ID′B, ID′C, and .

.

Without loss of generality, we assume that the probabilities that classical bits 0 and 1 occur are identical in every identity string. It means that states |0〉, |1〉, |+〉, and |−〉 have the same probabilities to be prepared for the decoy states. In addition, it is easily known that if measuring the particle 2 (3) from a GHZ state, one has the identical probability to get the results |0〉 and |1〉. This means in Table 1 the result that every row expresses has the same probability to appear.

It can be easily found that Eve has the probability of 5/16 to obtain the bits of IDB(IDC) definitely. Furthermore, we can calculate the average quantity of information Eve can gain about every bit of IDB (denoting by IEve→IDB).

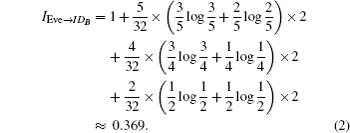
Similarly, the average quantity of information Eve can gain about every bit of IDC (denoting by IEve→IDC) is also 0.369.

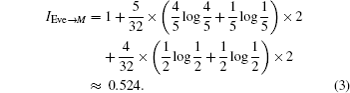
From Table 1, one can easily see that Eve has the probability of 7/16 to get the bits of CS2 (CS3) definitely. This means that Eve has the ability to get 7/16 of the secret message definitely according to the equalities M = C ⊕ CS2 = C ⊕ CS3. Moreover, one can calculate the quantity of information Eve can gain about every bit of the secret message on average (denoting by IEve→M).

So far, we have put forward an attack strategy for an external eavesdropper to get some information of IDB and IDC and the secret message M without being detected.

3.2. One receiver eavesdropping on the other’s identity string

If a receiver acts as an eavesdropper to eavesdrop on the other’s identity string, his attack obviously is more efficient because he has more resources and knowledge than the external eavesdropper. Here we take Bob as an example to eavesdrop on Charlie’s identity string IDC. The situation that Charlie eavesdrops on Bob’s identity string IDB is the same. The attack strategy is described as follows.

Rule 1 If a couple of the corresponding bits from DC and E3 are different, Bob can immediately deduce that he has measured a particle from S3, that is to say, IDC = 1. The reason is that if IDC = 0, then he has measured a decoy particle from SIDC according to Steps 2 and 3 of the QBC-CXZY protocol, and thus he knows that DC must be identical to E3.

Rule 2 If a couple of the corresponding bits from CS2 (CS3) and E3 are different, Bob can immediately deduce that he has measured a decoy particle from SIDC, that is to say, IDC = 0. This is because if IDC = 1, then he has measured a particle from S3, and he knows that CS2 (CS3) must be identical to E3.

To understand the above rules more unambiguously, we can refer to Table 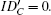2. Let us take the second row of Table 2 as an example. Because E3 ≠ CS2, Bob can deduce that

Table 2.

Using CS2 (CS3), DC, and E3 to deduce ID′C. In this table, represents the classical bit string about IDC that Eve can deduce; N represents that Eve cannot deduce the value confidently.

.

Without loss of generality, we assume again that the probabilities that classical bits 0 and 1 occur are identical in every identity string. It means that states |0〉, |1〉, |+〉, and |−〉 have the same probabilities to be prepared for the decoy states. In addition, it is easily known that if measuring the particle 2 (3) from a GHZ state with Z-basis, one has the identical probability to get results |0〉 and |1〉. This means in Table 2 the result that every row expresses has the same probability to appear.

From Table 2, one can easily see that Bob has the probability of 1/2 to get the bits of the identity string IDC definitely. That is to say, the quantity of information Bob can gain about every bit of the secret message on average is 1/2. Since 1/2 > 0.369, it shows that an inner receiver is more efficient than an external eavesdroppers to attack the identity string of the other receiver.

4. Discussion
4.1. An alternative attack strategy

As described above, Eve can make an intercept–measure–resend attack strategy to attack every particle labeled even in each traveling sequence. Actually, Eve can exploit an alternative strategy to attack the QBC-CXZY protocol (we call it the CNOT-operation attack). The concrete steps are as follows. Eve prepares an ancilla sequence in which each ancilla initially stays in |0〉. When a GHZ particle labeled even passes by, she performs a CNOT operation on this particle and an ancilla with the particle as the control qubit and the ancilla as the target, where

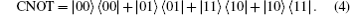
Then she measures each ancilla with Z-basis. The following steps are the same as described in Subsection 3.1. Also, one receiver can use this alternative strategy to eavesdrop on the other’s identity string as described in Subsection 3.2.

4.2. Cryptanalysis of the multi-party QBC-CXZY protocol

As for the multi-party QBC-CXZY protocol, an external eavesdropper can use the same attack strategy to eavesdrop on the receivers’ identity strings and the secret. The attack efficiency increases with the increase of the number of users. Now we will explain the reason in the following. For any i (2 ≤ i ≤ n), according to the knowledge of information theory, we have

i.e.,

Here, IDi, Dj, Ej(2 ≤ j ≤ n) represents the identity string of the i-th receiver (we let the sender be the first user), the classical bit string the j-th user can get by measuring the received decoy particles, and the classical bit string Eve can get by measuring the particles labeled even in the traveling sequence sent to the j-th user. I(X;Y) denotes the mutual information between X and Y.

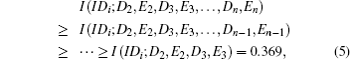
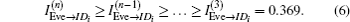
Similarly, the following inequalities hold.

i.e.,

Here CS is the classical bit string each receiver can get by measuring the received multi-qubit GHZ particles from the sender. Since I(CS; Dj, Ej) ≥ 1/4, one can easily know that

which means that

In particular, when n ≥ 17, It means that when the number of the users is not less than 17, Eve can get at least 0.99 bit of every bit of the secret message. So far, we have explained the reason why the attack efficiency increases with the increase of the number of users.

5. Improvement of the QBC-CXZY protocol

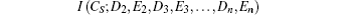
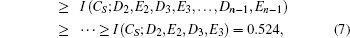
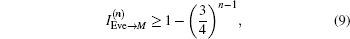
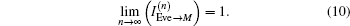
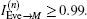
The reason why an external eavesdropper or an inner user can successfully make an intercept–measure–resend attack is that the identity strings of the receivers are used not only to prepare the decoy particles but also to determine how the decoy particles are mixed into the information carrier particles. That is to say, the identity strings are repeatedly used. This is not allowed in secure communication. Whether the particles labeled even in every traveling sequence are decoy particles or information carrier particles, they all will be measured with Z-basis according to the rules that the decoy particles are prepared and they are inserted into the information carrier particles. So Eve can use this drawback to make an attack without bringing any error. Therefore, to improve the QBC-CXZY protocol, every identity string should be used only once. So, Steps 3 and 4 of the QBC-CXZY protocol are changed as follows.

Step R3 Alice randomly mixes SIDB and SIDC to S2 and S3 to form S′2 and S′3 respectively. Apart from Alice, no one else knows how SIDB and SIDC are mixed into S2 and S3. After that, Alice transmits S′2 and S′3 to Bob and Charlie respectively.

Step R4 After Bob and Charlie receive S′2 and S′3, Alice publishes the information about which particles in S′2 and S′3 are decoy particles. That is, Alice tells Bob and Charlie which particles compose SIDB and SIDC respectively. Bob and Charlie extract SIDB and SIDC according to Alice’s announcement, and then they measure the particles in each sequence using the right bases respectively.

Note that, before Alice, Bob, and Charlie start a new communication, they will probably have to update the identity strings.

Now if an external eavesdropper or an inner receiver still exploits the intercept–measure–resend attack strategy to attack the particles labeled even in every traveling sequence, she (he) will introduce some errors. This is because the particles labeled even in each traveling sequence are not always staying in Z-basis or measured by the corresponding receiver with Z-basis.

6. Conclusion

In summary, we find that there are some security issues about the QBC-CXZY protocol. An eavesdropper can take the intercept–measure–resend attack strategy to eavesdrop on some information of the identity strings of the receivers and the secret message by measuring the particles labeled even in every traveling sequence with Z-basis without bringing any error. The reason why Eve can use this strategy to successfully attack is that whether the particles labeled even are decoy particles or information carrier particles, they all will be measured with Z-basis. This is really a serious drawback. Of course, an inner receiver can also take the intercept–measure–resend attack more efficiently than the external eavesdropper to eavesdrop on the other’s identity string without being detected. In addition, an alternative attack called the CNOT-operation attack is discussed. As for the multi-party QBC-CXZY protocol, the attack efficiency increases with the increase of the number of users. Finally, the QBC-CXZY protocol is improved to a secure one. In a word, more attention should be paid to the security of the quantum secure communication in order to design really secure quantum communication protocols.

Reference
1Bennett C HBrassard G1984IEEE International Conference on Computers, Systems & Signal ProcessingDecember 10–12Bangalore, India175
2Ekert A K 1991 Phys. Rev. Lett. 67 661
3Bennett C H 1992 Phys. Rev. Lett. 68 3121
4Bennett C HBrassard GMermin N D 1992 Phys. Rev. Lett. 68 557
5Bruβ D 1998 Phys. Rev. Lett. 81 3018
6Wang X B 2004 Phys. Rev. Lett. 92 077902
7Lo H KMa X FChen K 2005 Phys. Rev. Lett. 94 230504
8Boyer MKenigsberg DMor T 2007 Phys. Rev. Lett. 99 140501
9Noh T G 2009 Phys. Rev. Lett. 103 230501
10Tang Y LYin H LChen S JLiu YZhang W JJiang XZhang LWang JYou L XGuan J YYang D XWang ZLiang HZhang ZZhou NMa X FChen T YZhang QPan J W 2014 Phys. Rev. Lett. 113 190501
11Vazirani UVidick T 2014 Phys. Rev. Lett. 113 140501
12Deng F GLong G LLiu X S 2003 Phys. Rev. 68 042317
13Deng F GLong G L 2004 Phys. Rev. 69 052319
14Lucamarini MMancini S 2005 Phys. Rev. Lett. 94 140501
15Wang CDeng F GLi Y SLiu X SLong G L 2005 Phys. Rev. 71 044305
16Wang CDeng F GLong G L 2005 Opt. Commun. 253 15
17Deng F GLi X HLi C YZhou PZhou H Y2006Phys. Lett. A359
18Long G LDeng F GWang CLi X H2007Front. Phys. China2251
19Lin SWen Q YGao FZhu F C 2008 Phys. Rev. 78 064304
20Dong LXiu X MGao Y JChi F 2009 Opt. Commun. 282 1688
21Cao W FYang Y GWen Q Y 2010 Sci. China: Phys. Mech. Astron. 53 1271
22Gu BZhang C YCheng G SHuang Y G 2011 Sci. China: Phys. Mech. Astron. 54 942
23Liu Z HChen H WLiu W JXu JWang DLi Z Q 2013 Quantum Infor. Process. 12 587
24Hong C HHeo JLim J IYang H J 2014 Chin. Phys. 23 090309
25Li X H2015Acta Phys. Sin.640160307(in Chinese)
26Mi S CWang T JJin G SWang C2015IEEE Photon. J.77600108
27Beige AEnglert B GKurtsiefer CWeinfurter H 2002 Acta Phys. Pol. 101 357
28Yan F LZhang X Q 2004 Eur. Phys. J. B 41 75
29Man Z XZhang Z JLi Y 2005 Chin. Phys. Lett. 22 18
30Li X HDeng F GLi C YLiang Y JZhou PZhou H Y2006J. Korean Phys. Soc.491354
31Man Z XXia Y JAn N B 2006 J. Phys. B: At. Mol. Opt. Phys. 39 3855
32Xiu X MDong H KDong LGao Y JChi F 2009 Opt. Commun. 282 2457
33Quan D XPei C XLiu DZhao N2010Acta Phys. Sin.592493(in Chinese)
34Liu Z HChen H WLiu W JXu JLi Z Q 2012 Sci. China-Inf. Sci. 55 360
35Liu Z HChen H WWang DXue X L 2014 Int. J. Theor. Phys. 53 2118
36Li X HLi C YDeng F GZhou PLiang Y JZhou H Y 2007 Chin. Phys. Lett. 24 23
37Wang JZhang QTang C J 2007 Chin. Phys. 16 1868
38Yang Y GWang Y HWen Q Y 2010 Chin. Phys. 19 070304
39Chang YXu C XZhang S BYan L L 2014 Chin. Phys. 23 010305