† Corresponding author. E-mail:
We initially introduce one-dimensional mixed-five-spin chain with Ising-XY model which includes mixture of spins-1/2 and spins-1. Here, it is considered that nearest spins (1,1/2) have Ising-type interaction and nearest spins (1/2,1/2) have both XY-type and Dzyaloshinskii–Moriya (DM) interactions together. Nearest spins (1,1) have XX Heisenberg interaction. This system is in the vicinity of an external homogeneous magnetic field B in thermal equilibrium state. We promote the quantum information transmitting protocol verified for a normal spin chain with simple model (refer to Rossini D, Giovannetti V and Fazio R 2007 Int. J. Quantum Infor.
Transferring information between distinct systems is an important problem in quantum information theory. Many researchers involved themselves to investigate this problem carefully and tried to introduce some useful methods for better understanding transferring quantum states protocol theoretically (and practically in the futurity[1]) through ideal channels.[2–7] Recently, many profound studies have been devoted to quantum communication by using spin chains as suitable channels, and it was shown that transferring quantum information can be reliably achieved using chains of permanently coupled spins.[8–14]
Most works on quantum communication assume that channels have noise in transmission protocols, also somewhere, quantum channels with memory[7] have received considerable attention (The problem of quantum channels with memory was initially introduced in Ref. [2]). In the last two decades, quantum communication has not only been successful in characterizing these subjects but has also opened new problems. Another essential problem concerns the additivity of channel capacity when entangled states are used as signals to transfer quantum information.[15] It was proved that, quantum systems can be used for quantum communication channels[15,16] for carrying both classical[17,18] and quantum information.[5,19] Namely, different capacities for a quantum channel exist that must be separably defined. The classical capacity 𝒞[6,20,21] (also it has been mentioned of quasi-classical capacity in Ref. [21]) and the quantum capacity 𝓠[3,6,7,16,22] of a quantum channel are defined as the maximum number of bits and qubits respectively that can be reliably transmitted per channel use.
The transmission protocol can be conveniently described in terms of quantum operation formalism.[6,10,23,24] Hence, any input quantum state ρ is mapped onto the output state ρ′ = ℳ[ρ] via a linear completely positive trace preserving (CPTP) map ℳ. The simplest searchable models of quantum channels are the class of memoryless channels as ℳn = ℳ⊗n which describes n channel uses. In this paper, we confine ourselves to verify the quantum spin chains as memoryless channels with capacity. Furthermore, in the transferring quantum information process, efficiency of the communication can be characterized with the transmission rate 𝓡. This is a quantity which can be introduced as the maximum number of quantum states that one can transfer per unit of time with almost maximum fidelity (𝓕 ≈ 1) in the limit of large transmission time,[7,15,25] or in other words, the transmission rate can be (loosely speaking) defined as the fraction of states that can be recovered at the output with high fidelity over the total number of transmitted states.
Here, it should be noted that transmitting information by use of the spin systems is not restricted to the system evolution, in other words, one can also use the teleportation protocol (see review article[26]) and cloning for transferring quantum information. Cloning can be done commonly in classical systems, while for quantum systems it is not possible (due to the existence of the pure states). But on the other hand, we can try to clone a quantum state with almost maximum fidelity, or it can be ideally done with maximum probability. Cloning and teleportation protocols have been precisely investigated by Heng Fan et al. in Ref. [27].
From quantum information theory and quantum correlations view points, many investigations have been done on the mixture of coupled different spins with various models and many interesting results have been reported.[28–34] In the present work, we intend to introduce a new class of the quantum communication channels through which qutrits can be reliably transmitted as well as qubits. Hence, we use a mixed-five-spin chain with special Ising-XY model for which the nearest spins (1,1/2) have Ising-type interaction and nearest spins (1/2,1/2) have both XY-type and Dzyaloshinskii–Moriya (DM) interactions together. Nearest spins (1,1) have XX Heisenberg interaction, as a quantum communication channel then, investigate its quantum capacity and transmission rate 𝓡.
The outline of the paper is as follows. In Section 2 we introduce our favorite spin model with an analytical Hamiltonian. The transmission protocol is explained in Section 3. In Section 4, as a preliminary for review of the aforementioned quantities, we investigate quantum capacity and transmission rate for such a spin model as a communication channel according to the statements in Ref. [11]. Some numerical calculations and simulations are done in this section. Section 5 is devoted to summary and discussions.
We introduce a coupled mixed-M-spin chain with Ising-XY model (spin chain presented in Fig.

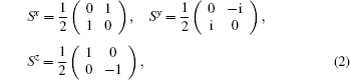

Assume that a quantum state ρ is propagated through a quantum channel, hence, we can characterize this propagation by a mapping protocol as

We explain the transmission protocol step by step in the following.
In the present work, a scenario is considered where the sender and the receiver use their spins belonging respectively to the first and last pairs’ spins (1,1/2) of the mixed-five-spin chain system for encoding and decoding information (classical or quantum). From the communication theory viewpoint, this consideration is not persuasive enough, but on the other hand, the consequences can be treated analytically.
For doing the transmission protocol, suppose that Alice has a memory with state |Ψ〉A = ··· |ψ3〉⊗|ψ2〉⊗|ψ1〉, where 
This procedure can be characterized as
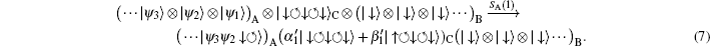


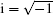
Quantum transmission rate for the introduced protocol in Fig.

The rate of this channel for ɛ used in the time interval T = ɛ τ can be defined as
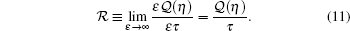
For our favorite mixed-five-spin system of the introduced model with Hamiltonian (

By setting Eq. (
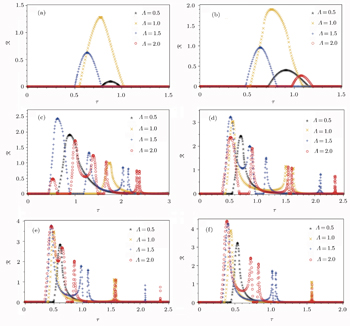
Figure 
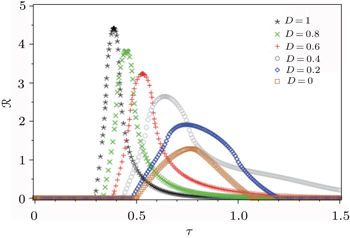 | Fig. 2. Transmission rate for the mixed-five-spin chain where the first element of Alice’s memory is state  |
With regard to this figure, for D = 0 (boxed diagram) transmission rate starts from τ = 0.5 and reaches its maximum amount at τ ≈ 0.75, then vanishes in τ ≈ 1.05. Here, we see a good compatibility between transmission rate of our favorite system at D = 0 and that represented in Ref. [11]. With increase of the DM interaction |D| (note that the transmission rate for D < 0 is the same for D > 0) from zero, transmission rate arises at the less time and reaches its maximum amount in the less time interval, but on the other hand, it vanishes at the longer time. It is clear that range of the maximum is proportional to |D|, namely, by increasing the DM interaction, the maximum amount of the transmission rate in addition to occur in the less time interval, increases.
Now, we investigate the transmission rate of the system when Alice prepares the state 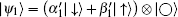

By substituting Eq. (
Transmission rate in the vicinity of a weak DM interaction D = 0.2 is shown in Fig.
In the introduction of this favorite model, we consider some irrelevant coefficients such as a homogeneous magnetic field B in the z direction, XY-type interaction for spin-half of any triangular cell and Ising-type interaction between spins (1,1/2) of any cell, which actually did not play any role to calculate and simulate the transmission rate, our motivation for citing them is introducing theoretically an upstanding spin system with a specific structure, by which its components have some special interactions together. Of course, by means of this citation, we interestingly realized that the transmission rate for this specific spin system is independent of the magnetic field B, anisotropy parameter γ, and Ising interaction coefficient J. It must be noted that these coefficients are ineffective until the initial state of the system is pure product state 
In this paper, we tried to introduce theoretically a new class of spin chain channel for transferring qutrits. In this way, we have introduced a one-dimensional mixed-five-spin chain with Ising-XY model which contains both permanently coupled spins-1/2 and spins-1 states. It has been assumed that nearest spins-1/2 have both XY-type and Dzyaloshinskii–Moriya (DM) interactions, nearest spins (1,1/2) have Ising-type interaction and nearest spins-1 (spins-1 of two adjacent triangular cells) have XX Heisenberg interaction. The system is in the vicinity of a homogeneous magnetic field and has an analytical Hamiltonian. Then, we have considered this system as a memoryless quantum communication channel with an initial pure product state and explained quantum information transmission protocol, in what follows we have calculated the quantum capacity of the channel and, finally, obtained the quantum information transmission rate.
According to our investigations, we concluded that for such a mixed-five-spin chain, the transmission rate is solely dependent on the DM interaction D between nearest spins-1/2 when the sender Alice prepared her memory with state 
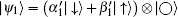
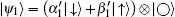
Therefore, if one chooses such a mixed-five-spin chain system with initial pure product state as a communication channel for transferring quantum qutrits states ideally, he (or she) should investigate the transmission protocol in the strong DM interaction regardless of existence of any magnetic field in the z direction, anisotropy related to the nearest spins-half and Ising-type interaction between nearest spins (1,1/2). Moreover, since the transmission rate of the suggested model is sensitive to the XX interaction between spins-1, use of this model as quantum communication channel might be more attractive.
It is more interesting to investigate this model with more spins (N > 2) and different interactions between its members. Also, one can verify the transmission rate for such a model but with mixed-six-spin which contains 3 spins-integer and 3 spins-half and gets some novel and attractive outcomes.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 |