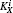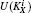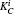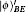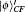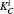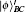† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61272495, 61379153, and 61401519) and the Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20130162110012).
A novel quantum dual signature scheme, which combines two signed messages expected to be sent to two diverse receivers Bob and Charlie, is designed by applying entanglement swapping with coherent states. The signatory Alice signs two different messages with unitary operations (corresponding to the secret keys) and applies entanglement swapping to generate a quantum dual signature. The dual signature is firstly sent to the verifier Bob who extracts and verifies the signature of one message and transmits the rest of the dual signature to the verifier Charlie who verifies the signature of the other message. The transmission of the dual signature is realized with quantum teleportation of coherent states. The analysis shows that the security of secret keys and the security criteria of the signature protocol can be greatly guaranteed. An extensional multi-party quantum dual signature scheme which considers the case with more than three participants is also proposed in this paper and this scheme can remain secure. The proposed schemes are completely suited for the quantum communication network including multiple participants and can be applied to the e-commerce system which requires a secure payment among the customer, business and bank.
Quantum cryptography is a new cryptosystem which combines quantum theory with classical cryptography.[1] Because it is based on the Heisenberg uncertainty principle and quantum no-cloning theorem,[2] it has provable security. Quantum cryptography includes a lot of branches, such as quantum key distribution (QKD), quantum secret sharing (QSS), quantum identification (QI), quantum secure direct communication (QSDC), quantum signature (QS), quantum encryption algorithm (QEA), etc.
A QS is considered as the additional information to the message for the purpose of preventing the message from being forged or tampered with.[3] It is based on the physical properties which provide unconditional security and is one of the most important ways to realize identity and message authentication. QSs are classified into two categories, i.e., arbitrated quantum signatures (AQSs) and true quantum signatures (TQSs). An AQS always needs the participation of a trusted arbitrator. However, only in the case of dispute, a TQS requires a trusted arbitrator. Moreover, a QS algorithm must follow three principles, namely, non-forgery, non-repudiation, and quantum properties.
So far, scholars and researchers have proposed a lot of quantum signature schemes. In accordance with quantum one-way functions and quantum swap-test, Gottesman and Chuang first presented a quantum digital signature protocol in 2001.[4] In 2002, Zeng and Keitel put forward a signature scheme based on the Greenberger–Horne–Zeilinger (GHZ) triplet states, whose realization depends upon a trusty arbitrator.[1,5,6] In 2007, Wen and Liu presented a quantum signature protocol without the participation of the arbitrator.[7] Then Zeng et al.[3] presented a true quantum signature protocol based on a continuous variable entangled state in the same year. Shi et al. proposed a multiparty quantum proxy group signature scheme[8] in 2011 and a (t,n)-threshold quantum group signature scheme[9] in 2012 which are both based on quantum Fourier transform. In 2013, Shi et al.[10] presented a batch proxy quantum blind signature scheme with three-dimensional two-particle-entangled quantum-trits. In 2014, Dunjko et al.[11] introduced a quantum digital signature scheme, which applies coherent states without quantum memory. In 2014, Chao et al. investigated the cryptanalysis and the corresponding improvements of the previous proposed AQS schemes, and constructed a novel enhanced AQS scheme.[12] Recently, Shang et al.[13] first proposed a quantum homomorphic signature protocol by using entanglement swapping, which is used to authenticate data packets of multiple streams for quantum networks.
However, the signature protocols mentioned above either utilize discrete variables, or consider the situation for only one message. It is known that the transmission efficiency of discrete-variable protocols is much lower than that of continuous-variable protocols, and a single photon for the discrete variable is detected with difficulty. Thus the efficiency of signature protocols is expected to be improved with continuous variables. The coherent state is one of the continuous-variable states and it is the quantum state which is closest to the classical state. The entangled coherent state (ECS) which is made up of coherent states is wildly exploited in quantum information processing.[14–16] There are two advantages of the ECS. On one hand, the ECS is robust to decoherence caused by the absorption of photons.[17] On the other hand, quantum information processing based on the ECS can be achieved with existing experimental techniques, such as linear optics. What is more, the multi-signature requirement in the quantum communication network which involves multiple participants should be taken into consideration as well. In the e-commerce system, a classical dual signature can be utilized for realizing the connection of two different messages.[18,19] In detail, the dual signature, which combines the customer’s order information and payment information that are encrypted with separate secret keys, can be used to solve the problem that the customer’s order information (payment information) should be hidden to the bank (business) while the payment information should be blindly forwarded to the bank by the business.
Inspired by the dual signature schemes and the advantages of continuous variables, a new quantum dual signature scheme based on coherent states with entanglement swapping[20–22] is proposed in this paper. Compared with these discrete-variable schemes, the message and signature states in our scheme are convenient to generate and operate. Specifically, the quantum dual signature is generated by combining two signed messages with entanglement swapping. The information transmission in our scheme takes advantage of quantum teleportation of coherent states.[23,24] Our proposed scheme is absolutely satisfied with the security criteria of the signature protocol.
The main contributions of this paper are presented below.
The rest of this paper is organized as follows. In Section 2, we introduce the beam splitter with coherent states. Section 3 describes the quantum dual signature algorithm including the initial phase, the signing phase, and the verification phase. The security of the proposed scheme is analyzed in Section 4. The quantum dual signature scheme which involves more than three participants is discussed in Section 5. Finally, conclusions are drawn in Section 6.
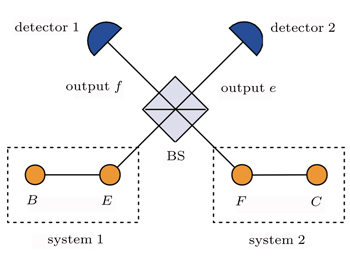
Beam splitters (BSs) are the most commonly applied optical components.[24,25] They are passive components which do not need external energy and can actually operate in the laboratory. The BS couples incident lights or generates two light beams with the same frequency. A loss-less 50:50 BS is denoted with
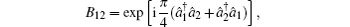
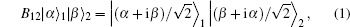
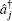
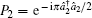
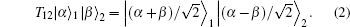
This is a significant operation which can be used to generate ECSs. Generally, the bipartite ECS[27] with two modes of the electromagnetic field is described as
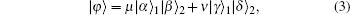
Based on Eq. (

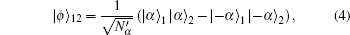
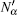
Generally, we consider the following four two-mode ECSs[28] as quasi-Bell states, i.e.,
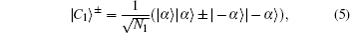

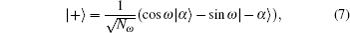
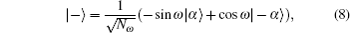


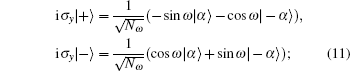
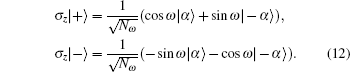
The above operations of BSs are important to most of the quantum information processes which involve the coherent states. Additionally, ECSs are easier to detect. Therefore, we present the following quantum dual signature scheme based on the properties of ECSs and BSs.
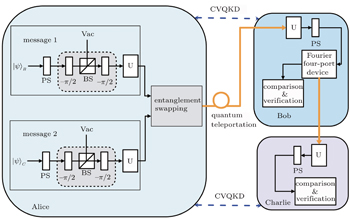
The schematic representation of the propounded scheme is shown in Fig.
In this phase, Alice generates coherent superposition states, encodes her own message states with the secret keys and acquires corresponding ECSs. The procedures are described below.

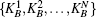
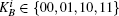
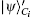
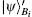
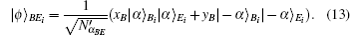

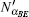
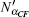
This phase gives a specific description of the signature algorithm, i.e., Alice signs the message states by implementing unitary operations and merges these signed messages into a dual signature in the network. The technique used here is entanglement swapping which enables two parties that do not share quantum entanglement to share quantum entanglement with the assistance of a third party.[20] The signing phase is carried out by the following procedures.
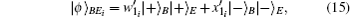
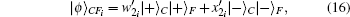
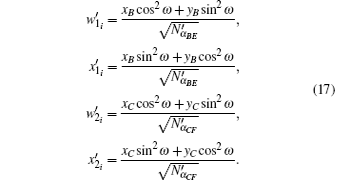

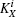
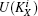
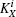
| Table 1. The corresponding relationship between the operations and the secret keys. . |
Then Alice implements the corresponding operation on state |ϕ〉BEi and derives the signature

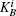

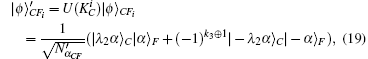
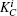
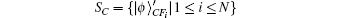
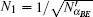
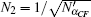
| Table 2. Alice’s signatures based on different secret keys. . |
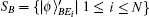
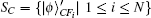
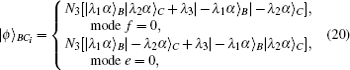
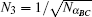
The verification phase requires Bob (Charlie) to verify the signatures of message 1 (message 2) and judge whether the message states are authentic. This process does not need the participation of the arbitrator, unless there are controversies.
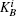
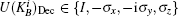
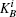
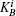
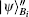
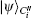
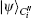
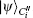

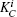
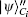
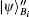
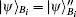
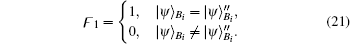
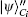

So Bob (Charlie) can draw a conclusion whether the signature is acceptable based on the parameter ϝ1 (ϝ2).
For the purpose of guaranteeing the security, the quantum signature scheme should satisfy two requirements.[36] One is that the attacker and the disingenuous receiver cannot forge the signature after the completion of signing, and the other is the signatory and the receiver cannot disavow the signature. On the basis of the above security requirements of quantum signature scheme, our protocol provides theoretical security since the attacker cannot obtain the useful information about the secret key and the original message, the signatory is unable to disavow the signatures and the verifiers also cannot deny the received signatures. Subsequently, we analyze the security of the proposed scheme in detail.
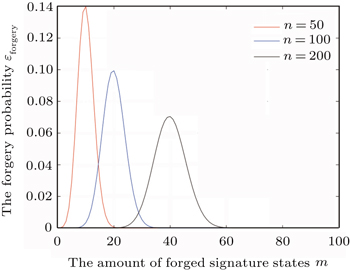
According to our signature scheme, the two signatures of Alice are SB and SC, separately. If the attacker Eve attempts to forge Alice’s signatures, she has to be aware of the corresponding secret keys KB or KC. For the attacker, there are two ways to get the information about secret keys, i.e., she eavesdrops in the key distribution phase or obtains it from the signature.
However, due to the unconditionally secure CVQKD,[37–41] it is impossible to eavesdrop the secret keys shared between the signatory and verifiers. Moreover, quantum one-time pad algorithm also ensures the security. On one hand, for preventing the recipient or the eavesdropper from forging a message in the quantum signature process, we should ensure that only Alice knows the complete information about message states. If the attacker obtains the signature, she is ignorant of the signature algorithm. Thus Eve cannot infer the secret key from the signature. On the other hand, according to the characteristics of entanglement, once Eve tries to measure the signature to get the information of the keys, the entangled state may collapse and the forgery behavior can be discovered definitely and then honest correspondents may give up this communication. So Eve fails to deduce the key.
In the worst situation, if Eve gets KB (KC), she still has no information about the message states that were distributed to Bob (Charlie) without destroying the entanglement states. Moreover, if Eve tampers with the signature, the following example shows that the forgery can be definitely detected.
Comparing Eq. (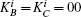

| Table 3. The quantum dual signatures under different conditions. . |
If the receiver Bob is malicious and attempts to forge Alice’s signature, he is obliged to know Charlie’s secret key KC. However, his forgery fails since he cannot obtain the secret key KC and has no idea of message 2. Besides, Charlie cannot forge the signature of message 1 since he has no chance of access to message 1’s signature. He also could not forge message 2’s signature, because he knows nothing about the message states of message 2. Based on the analysis, we can conclude that any forgery would fail.
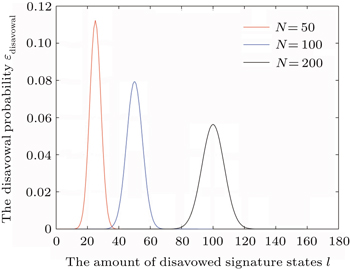
In the proposed scheme, Alice signs messages 1 and 2 and integrates the two signatures to generate a dual signature, which includes the information of KB (KC) that is only distributed between Alice and Bob (Charlie). Thereby, it is easy to discover whether Alice disavows the signature or not. Furthermore, Alice may either recognize or disavow the signature, so the probability of disavowing a signature state is 1/2. Thus the probability of disavowal for the signature by Alice is
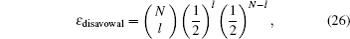
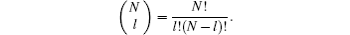
In particular, when there are disputations between signatory and verifiers, a trusted arbitrator is required. Alice just needs to transmit her messages and the corresponding signatures to the arbitrator. For example, if the signature which belongs to Alice can be decoded by Alice’s secret key, the signature has been executed by Alice, otherwise, Bob, Charlie or the attacker has forged the signature. It is apparent that the arbitrator plays an important role in judging whether Alice has disavowed her signatures when there are disputes or disagreements.
The verifier Bob cannot deny his behavior. After the operation of entanglement swapping, Alice sends the dual signature SBC to Bob. It is clear that Bob knows the secret keys KB and he performs some operations on the dual signature during the verification phase. He is willing to verify the signature meaning that he received the dual signature which contains information of Alice’s signatures, and he has verified the signature indeed without later denying his involvement and actions. In the same way, Charlie also fails to deny. Based on KC, Charlie performs measurements and operations after receiving the signature of message 2. So he cannot deny his behaviors.
According to the above analysis, we can determine that the proposed signature scheme can provide us theoretical security.
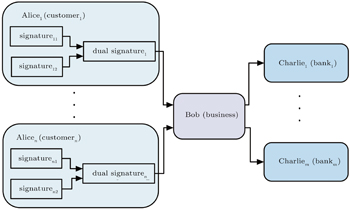
In the real life, a merchant often trades with some multiple customers and every customer has several different bank accounts. Thus the quantum dual signature scheme which contains more than three participants is discussed in this section. As shown in the following Fig.
The multi-party quantum dual signature scheme also includes three phases, i.e., the initial phase, the signing phase and the verification phase. The main difference between the multi-party quantum dual signature scheme and the three-party one is that Alicei needs to notify Bob of the trading bank in advance in the initial phase. We assume that Alicei wants to pay the order with her account in the bank Charlie j. The extensional scheme is briefly described as follows.
The unconditional security of our extensional scheme can also be guaranteed. Moreover, it is obvious that the multi-party quantum dual signature scheme is preferably applicable to the network. It also has the important application value in the e-commerce system for its unconditional security.
A quantum dual signature scheme based on the ECSs and entanglement swapping is presented in this paper, in which a signatory and two verifiers are considered. The signatory Alice signs two different messages 1 and 2 which are separately sent to two diverse verifiers Bob and Charlie. Alice aggregates those two signatures to generate a quantum dual signature with entanglement swapping. In order to make this scheme suitable for the practical application, the signature verified by Charlie is forwarded by Bob. The verifier Bob (Charlie) can judge whether the signature of message 1 (2) is authentic and valid. Based on the security analysis with quantum properties, any attacker who attempts to counterfeit the signature would be detected, and the important rules impossible to forge, disavow or deny for the signature protocol are observed, thus our protocol can guarantee the security unconditionally. The three-party scheme can also be extended to the multi-party scheme which contains more than three participants, and the extensional scheme can remain safe. Furthermore, the proposed schemes are quite appropriate for the e-payment system if they involve further theoretical and technical supports.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 |