† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11174052 and 11474049) and the China Advanced Science and Technology Innovation Fund.
We show a scheme of preparing multipartite W type of maximally entangled states among many atomic ensembles with the generation time increasing with the party number only polynomially. The scheme is based on laser manipulation of atomic ensembles and single-photon detection, and fits well the status of the current experimental technology. We also show one of the applications of this kind of W state, demonstrating Bell theorem without inequalities.
Entanglement has been studied very extensively as it impacts both foundational as well as applied aspects of quantum theory.[1] Moreover, multi-partite entanglement plays a central role in a host of quantum technologies, including metrology, imaging, communication, and quantum information processing.[2–8] Many schemes for generation of the multi-particle entangled state have been proposed.[9–19] Among all the physical systems which have been considered for generating multi-particle entangled states, atomic ensembles are well developed and regarded as ideal candidates for quantum information processing, especially for quantum state engineering. Recently, breakthrough experimental achievements on atomic ensembles[20–27] have been reported, which attracts more attention to this physical system.
We present a scheme of preparing multipartite W type of maximally entangled states among many atomic ensembles with the generation time increasing with the party number only polynomially. In addition, a proof of Bell theorem[28] without inequalities specifically for the W states can be realized experimentally. The scheme involves the following features: firstly, it is robust to realistic noise and imperfections. As a result, the physical requirements of this scheme are moderate and well fit the experimental technique. Secondly, in contrast to the belief that an entanglement preparation scheme based on post-selection will suffer from the fast exponential degradation of the efficiency,[9,10] we design this scheme with an efficient scaling and make it possible to maximally entangle many ensembles with the current technology. Finally, by making use of quantum memory available in atomic internal levels, the W states can be put into many applications such as demonstrating quantum non-locality, and a quantum channel for perfect teleportation.[29]
Let us have a look at the generalized form |WM〉 of the W state in multi-qubit systems. In Ref. [30], the state is defined as
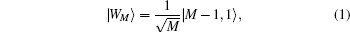
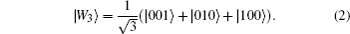
The basic element of this scheme is an ensemble of many identical alkali atoms with a Raman type Λ-level configuration coupled by a pair of optical fields, shown as Fig.
The experimental realization can be either a room-temperature dilute atomic gas[31–33] and a sample of cold trapped atoms.[34,35] We continue to use the symbols and corresponding definitions shown in Refs. [36] and [37]. There are two kinds of laser pulses (pumping laser and repumping laser) applied to the atomic ensembles, which correspond to Raman transition |g〉 → |s〉 and anti-Raman transition |s〉 → |g〉, respectively. A weak pumping laser is shone on all atoms so that each atom has an equal small probability to be excited into the state |s〉 through the Raman transition. After the atomic gas interacts with the pumping laser, there will be a special atomic mode Ŝ called the symmetric collective atomic mode

Firstly, the three atomic ensembles are prepared to the ground state |g〉, i.e., |vac〉123 = |vac〉1 ⊗|vac〉2 ⊗|vac〉3 and illuminated by the classical pumping laser pulses instantaneously. Each ensemble will be excited to be in the state Ŝ†|vac〉 with probability pc. The forward scattering Stokes photons from optical excitations of the ensembles are combined at the three BSs with transmittances and reflectances Ti and Ri (here i = 1,2,3, and 
If the detector D1 clicks, the state of the atomic ensembles is given in


Otherwise, if D3 clicks, the ensembles are put in the state shown as

Once the transmittances and reflectances of the BSs are chosen as 

To realize an arbitrary ratio of transmittance and reflectance of the BSs experimentally, one only needs to add a tunable quarter-wave plate (QWP) and half-wave plate (HWP) in front of the 50/50 BS, changing the circular polarization of the Stokes photons from optical excitation into linear polarization. That is, the Stokes photons are in T|H〉+eiφR|V〉, where H and V, respectively, represent the horizontal and vertical polarizations, and T, R, and φ are fixed by the relative inclination between the optical axes of the QWP and HWP. The outputs go through a polarizing beam splitter (PBS) before the single-photon detectors. By adjusting the optical axes of the QWP and HWP, one can obtain an arbitrary ratio of the Stokes photons from the optical excitation with the horizontal and vertical polarizations, respectively.
The scheme of generation of three-particle W-type entangled states can be extended to generate n-particle W states via BSs with proper transmittances and reflectances. If either of the detectors Di (i = 2,…,n) clicks, the rest and D1 do not click, we obtain an n-particle W state |Wn〉.
Now we calculate the efficiency of this scheme for preparing three-party W state. In the generation process, the dominant noise is the photon loss, which includes the contributions from the channel attenuation, the spontaneous emissions in the atomic ensembles, the coupling inefficiency of Stokes light into and out of the channel, and the inefficiency of the single-photon detectors which cannot perfectly distinguish between one and two photons. All the above noise is described by an overall loss probability η. Since the dominant realistic noise — loss of excitations — only has influence on the success probability to register an excitation from each ensemble, once the excitation is registered, we obtain a perfect W state (
Also with the noise, the state of the ensembles is actually described by

We briefly discuss the practical implication of this proposal. With the improved scheme, for example, we can generate a high fidelity W entanglement over n = 20 ensembles in a time T ∼ 300 μs with a notable loss η ∼ 1/3 and a typical choice of pc ∼ 0.01, tΔ ∼ 1/fp, where fp = 10 MHz is the repetition frequency of the Raman pulses. With such a short preparation time, the noise that we have not included, such as the non-stationary phase, drift induced by the pumping laser or by the optical channel, the single bit rotation error (< 10−4) and the dark count probability (about 10−5 in a typical detection time window 0.1 μs) of the single-photon detectors can be negligible.
Since the W state shown in Eq. (
The first step is to share an EPR type of entangled state
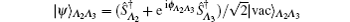




The preparation of the EPR state is probabilistic, however, due to the available quantum memory provided by the meta-stable atomic mode Ŝ, the preparation time of the state is at most 3t0 if the EPR states are prepared one by one, and can be reduced to t0 if the EPR states are prepared independently at the same time. Also, the W state is prepared synchronously with the generation time t1 > t0. After the preparation of the product state, the projection efficiency (success probability) from the product state to the effective “polarized” W state is given by (1 − η)3/8. So the total time from registering the three-party “polarized” W entanglement is T ∼ 8t1/(1 − η)3.
To demonstrate quantum non-locality, firstly, we perform an operation “σx” on each of the three qubits resulting in the value xΛ ∈ {1, −1} with equal probability. The repumping lasers with the frequencies ωrepump are applied on the ensembles Λ1 and Λ2, respectively, and the outputs are combined at the 50/50 BSs. We only consider the cases in which there is one excitation on each pair of ensembles Λ1 and Λ2. If a forward scattering Stokes photon is detected by the detector 
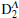
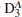


Finally, we have a brief conclusion. In this paper, we describe a scheme of preparation of entangling many atomic ensembles in the W type of maximally entangled states through laser manipulation. Remarkably, the generation time increases with the party number only polynomially. Due to the efficient scaling of this scheme, one can use it to steadily entangle many atomic ensembles in the W state with the current experimental technology. Hence, such an extraordinary possibility opens up prospects for many exciting experiments and applications.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 |





