Cite this Article
Yazarloo B H, Mehraban H, Hassanabadi H. Non-relativistic scattering amplitude for a new multi-parameter exponential-type potential. Chinese Physics B, 2016, 25(8): 080302  
Permissions
Non-relativistic scattering amplitude for a new multi-parameter exponential-type potential
Yazarloo B H1, †, , Mehraban H1, Hassanabadi H2
Physics Department, Semnan University, P. O. Box 35195-363, Semnan, Iran
Physics Department, Shahrood University of Technology, Shahrood, Iran

 

† Corresponding author. E-mail: h.yazarloo@students.semnan.ac.ir

Abstract
Abstract

In this paper, we study the scattering properties of s-wave Schrödinger equation for the multi-parameter potential, which can be reduced into four special cases for different values of potential parameters, i.e., Hulthén, Manning–Rosen, and Eckart potentials. We also obtain and investigate the scattering amplitudes of these special cases. Some numerical results are also obtained and reported.

PACS: 03.65.–w;03.65.Nk
Keyword:scattering amplitude;Schröodinger equation;multi-parameter potential;phase shifts;cross section
1. Introduction

One of the important tasks of non-relativistic or relativistic quantum mechanics is to study the bound states and scattering properties of a given quantum mechanical system under the action of a potential, which is very useful in studying the physical properties and handling the necessary information about the system. Recently, several authors introduced different potential models to explore the non-relativistic/relativistic bound states and scattering properties.[1–3] Aydoğdu et al.[4] derived the scattering and bound states of the Klein–Gordon equation for the Hulthén potential with unequal scalar and vector potentials and considered the position-dependent mass and constant mass, as a special case. They also calculated the transmission and reflection coefficients. In the case of unequal scalar and vector potentials, Wei et al.[5] obtained the phase shifts and normalization constant of the Klein–Gordon equation for Hulthén potential by introducing an improved new approximate scheme into the centrifugal term. The authors in Ref. [6] also reported the normalized radial wave functions and obtained the analytical formula of phase shifts within the framework of the partial-wave method, for the Schrödinger equation under the hyperbolic molecular potential. Castilho and Castro[7] investigated the scattering and bound states of fermions in a mixed vector–scalar smooth step potential. In D-dimensional space, Chen et al.[8] represented the non-relativistic scattering properties of modified Pöschl–Teller potential. They also provided some numerical results and compared them with others. In view of a spatially one-dimensional (1D) Woods–Saxon potential, the scattering solutions of the Klein–Gordon equation have been obtained in terms of hypergeometric functions by Rojas and Villalba, and they have derived the condition for the existence of transmission resonances.[9] The interested readers can also consult Refs. [10]–[12] for more information.

Recently, Garcia-Martinez[13] proposed the solvable multi-parameter exponential-type potential in the following form:

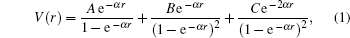
where A, B, and C are the potential parameters, and α is the screening parameter. The choices of the A, B, and C parameters lead to specific exponential-type potentials. The Hulthén, Manning–Rosen, and Eckart potentials are special cases of the multi-parameter exponential-type potential. The non-relativistic scattering states of Hulthén and Manning–Rosen potentials can be found in Refs. [14] and [15], respectively.

The main purpose of the present article is to report the scattering amplitude of the s-wave Schrödinger equation for the multi-parameter exponential-type potential and to discuss the special cases of the potential.

2. Scattering amplitude of the multi-parameter exponential-type potential

The radial Schrödinger equation has the form

Substitution of multi-parameter exponential-type potential converts the radial Schrödinger equation into the form (for l = 0)

By introducing a new variable z = 1 – e−αr, equation (3) is transformed into the form

Substituting Rn(z) = zξ1 (1 – z)ξ2 Gn(z) into Eq. (4) leads to

where

Equation (5) can be written as

The solution of Eq. (8) is well known, and it is expressed as hypergeometric function

where

So the radial wave functionRn(r) can be obtained as

and Nn is the normalization constant. To obtain a finite solution, γ1 or γ2 must be a negative integer. This gives the following equations:

where, n is the quantum number and the energy eigenvalue equation can be found from the above equation. By using the properties of hypergeometric function

for r → ∞, 2F1 (γ1, γ2, γ3; 1 – e−αr) can be written as

Inserting Eq. (16) into Eq. (13) gives

The asymptotic behavior for the wave function is given by[16,17] (for l = 0)

By comparing Eq. (17) with Eq. (18), we find

or equivalently, from Eqs. (10)–(12), we can easily obtain

Therefore, the total cross section can be easily obtained from

where

3. Some special cases

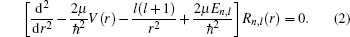
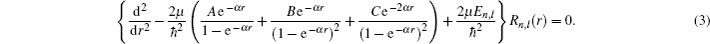
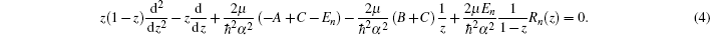
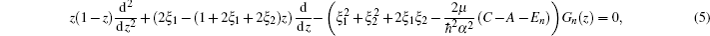
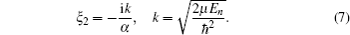
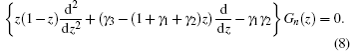
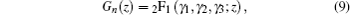
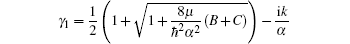
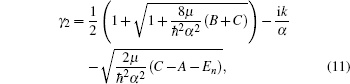
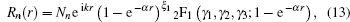
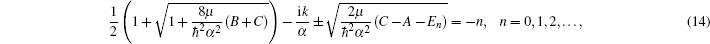
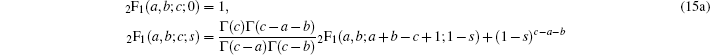
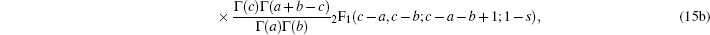
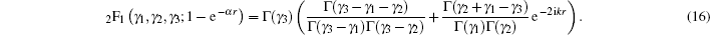
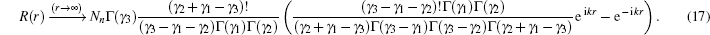
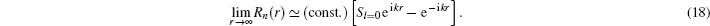
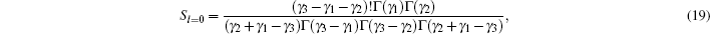
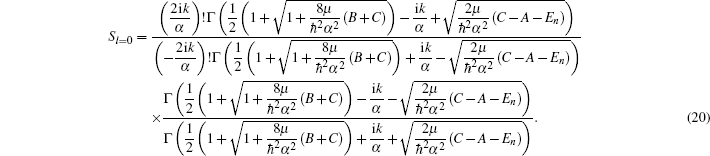
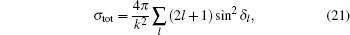
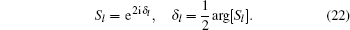
In this section, we are going to study four special cases of the multi-parameter exponential-type potential and their scattering properties by choosing approximate parameters in the multi-parameter exponential-type potential.

3.1. Hulthén potential

As already mentioned, for A = −Ze2λ, α = λ, B = C = 0, the multi-parameter exponential-type potential reduces to the Hulthén potential

where λ is the screening parameter and Z is a constant identified with the atomic number. The Hulthén[18] potential is one of the significant exponential potentials, which behaves like a Coulomb potential for small values of r and decreases exponentially for large values without having the problems of the former, and it has many applications in different areas of physics.[19–21] According to Eqs. (6), (7), and (10)–(12) we have

Therefore, from Eq. (20) we obtain

3.2. Manning–Rosen potential

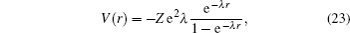
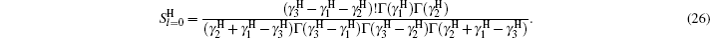
If we choose B = 0, A = −V0/b2, C = α′(α′ – 1)/b2, and α = 1/b, the multi-parameter exponential-type potential turns into the Manning–Rosen potential[22,23]

The Manning–Rosen potential was first introduced by Manning and Rosen[24] in 1933. It is used for describing the diatomic molecular vibrations. From Eqs. (6), (7), and (10)–(12), one can obtain

and the scattering amplitude, from Eq. (20), is

3.3. Eckart potential

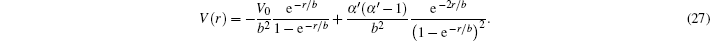
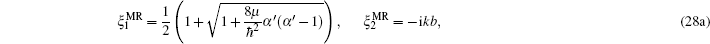
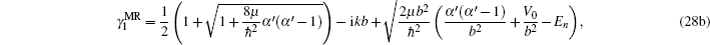
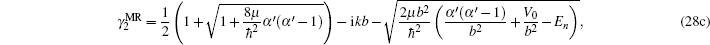
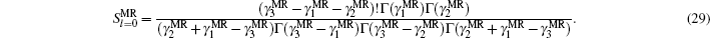
By considering C = 0, A = −δ, B = β, α = 1/a, the multi-parameter exponential-type potential changes into the Eckart potential

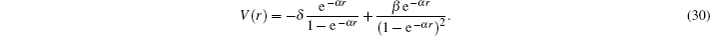
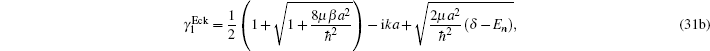
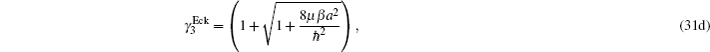
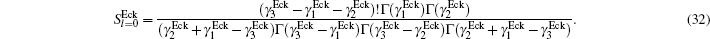
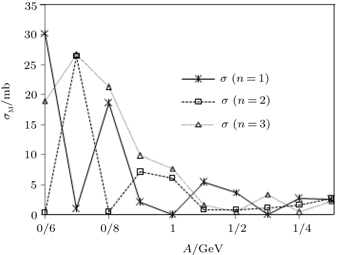
The Eckart potential[25] is one of the most important exponential-type potentials in the literature and it has many applications in different areas.[16,26] According to our results, we have

thus from Eq. (20) we obtain

Finally, we present some figures which show the scattering cross section (σ) of multi-parameter exponential-type potential and its special cases for different states in Figs. 1–4.

Fig. 1. Variations of scattering cross section with A for different states of multi-parameter exponential-type potential, C = 0.09 GeV, m = 0.938 GeV, B = 0.2 GeV, and α = 0.01 GeV. The unit 1 b = 10−28 m2.
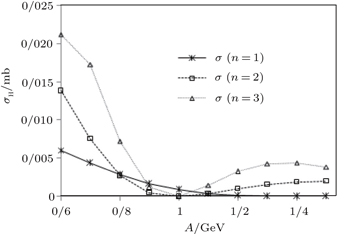Fig. 2. Variations of scattering cross section with A for different states of Hulthén potential m = 0.938 GeV and α = 0.01 GeV.
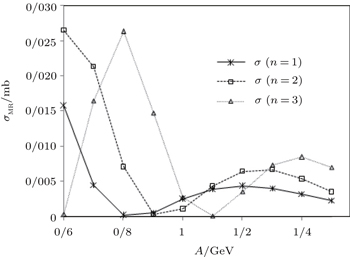Fig. 3. Variations of scattering cross section with A for different states of Manning–Rosen potential, C = 0.0002 GeV, m = 0.938 GeV, and α = 0.01 GeV.
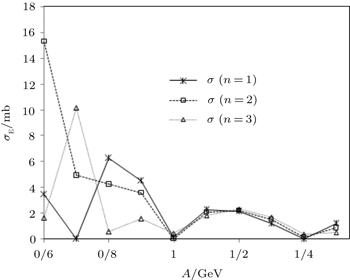Fig. 4. Variations of scattering cross section with A for different states of Eckart potential, m = 0.938 GeV, B = 0.2 GeV, and α = 0.01 GeV.

It is obvious from these figures that among the special cases of the multi-parameter exponential-type potentials, the Eckart potential has made the most contributions to cross section, and the obtained values of the cross section for this potential are greater than for the Hulthén and the Manning–Rosen potentials. We can also see that in Fig. 4, the cross section of the Eckart potential at A = 1 GeV and A = 1.4 GeV have minimum values for all the states.

4. Conclusions

The multi-parameter exponential-type potential provides an appealing option for theoretical physicists especially for molecular systems. As we have already mentioned, this potential can reduce to special cases of molecular potentials, therefore it can be a suitable choice to study physical systems. Because of these results and the importance of scattering properties, we investigate the scattering amplitude of the Schrödinger equation for multi-parameter exponential-type potential, and report the scattering amplitudes of the special cases. We also report some numerical results. As we see from the figures, of the three potentials (the Eckart potential, the Hulthén potential, and the Manning–Rosen potential), the Eckart potential makes the most contributions to cross section.

Reference
1Lu B NZhao E GZhou S G 2012 Phys. Rev. Lett. 109 072501
2Guo J YChen S WNiu Z MLi D PLiu Q 2014 Phys. Rev. Lett. 112 062502
3Zhou YGuo J Y 2008 Chin. Phys. 17 380
4Aydoğdu OArda ASever R 2012 J. Math. Phys. 53 102111
5Wei G FLiu X YChen W L 2009 Int. J. Theor. Phys. 48 1649
6Wei G FChen W LDong S H 2014 Phys. Lett. 378 2367
7Castilho W Mde Castro A S 2014 Ann. Phys. 346 164
8Chen C YLu F LYou Y 2012 Chin. Phys. 21 030302
9Rojas CVillalba V M 2005 Phys. Rev. 71 052101
10Yazarloo B HLu L LLiu GZarrinkamar SHassanabadi H2013Adv. High Energy Phys.2013317605
11Zarrinkamar SForouhandeh S FYazarloo B HHassanabadi H 2013 Eur. Phys. J. Plus 128 109
12Hassanabadi HYazarloo B HHassanabadi SZarrinkamar SSalehi N 2013 Acta Phys. Pol. 124 20
13Garcia-Martinez JGarcia-Ravelo JMorales JPena J J 2012 Int. J. Quantum Chem. 112 195
14Arda AAydoğdu OSever R 2011 Phys. Scr. 84 025004
15Chen C YLu F LSun D S 2007 Phys. Scr. 76 428
16Cooper FKhare ASukhatme U 1995 Phys. Rep. 251 267
17Yadav R KKhare AMandal B P 2013 Ann. Phys. 331 313
18Zarrinkamar SRajabi A AYazarloo B HHassanabadi H 2013 Chin. Phys. 37 023101
19Lam C SVarshni Y P 1971 Phys. Rev. 4 1875
20Hulthén LSugawara MFlugge S1957Handbuch der PhysikBerlinSpringer-Verlag
21Berezin A A 1972 Phys. Status Solidi 50 71
22Wang P QZhang L HJia C SLiu J Y 2012 J. Mol. Spectrosc. 274 5
23Liu J YZhang G DJia C S 2013 Phys. Lett. 377 1444
24Manning M FRosen N1933Phys. Rev.44953
25Eckart C 1930 Phys. Rev. 35 1303
26Weiss J J 1964 J. Chem. Phys. 41 1120