Charge-density-wave (CDW) order usually exists in some low-dimensional materials, especially those transition-metal chalcogenides.^[1–4] When the CDW order is suppressed by doping or pressure, a list of them can be tuned to superconductors.^[5–8] In the temperature–doping (T–x) or temperature–pressure (T–p) phase diagram, sometimes a superconducting dome is observed on top of a CDW quantum critical point (QCP).^[5–8] The reminiscent of this kind of phase diagram to that of the heavy-fermion and high-T_c cuprate superconductors raises the possibility of unconventional superconductivity caused by CDW fluctuations.^[5–9]

ZrTe₃ is such a compound in which the CDW order and superconductivity compete and coexist.^[10] It belongs to a family of trichalcogenides MX₃ (M = Ti, Zr, Hf, U, Th, and X = S, Se, Te). The structure consists of infinite X–X chains formed by stacking MX₃ prisms.^[11] The polyhedra are arranged in double sheets and stacked along the monoclinic c axis by van der Waals forces.^[11] Pristine ZrTe₃ itself harbors filamentary superconductivity with T_c ∼ 2 K.^[10] The CDW vector q ≈ (1/14; 0; 1/3) is developed in ZrTe₃ below T_CDW ∼ 63 K.^[12] Like other CDW materials, pressure and doping can melt the CDW order and stabilize its superconductivity to bulk.^[13–16] Recently, isovalent substitution of Se for Te was also found to cause a superconducting dome in the ZrTe_3−xSe_x system, with maximum T_c = 4.4 K at the optimal doping x = 0.04.^[17] It was suggested that this superconductivity may be mediated by quantum critical charge fluctuations.^[17] To clarifying the underlying pairing mechanism, it is important to know the superconducting gap symmetry and structure.

Ultra-low-temperature heat transport is an established bulk technique to probe the superconducting gap structure.^[18] The existence of a finite residual linear term κ₀/T in zero magnetic field is an evidence for gap nodes.^[18] The field dependence of κ₀/T may further give support for a nodal superconducting state, and provide information on the gap anisotropy, or multiple gaps.^[18]

In this paper, we measure the ultra-low-temperature thermal conductivity of ZrTe_3−xSe_x single crystals near optimal doping to investigate whether the superconducting state is unconventional. The negligible κ₀/T in zero field and the rapid field dependence of κ₀(H)/T in low field strongly suggest multiple nodeless superconducting gaps in ZrTe_3−xSe_x. In this sense, the superconductivity in ZrTe_3−xSe_x is likely conventional.

The ZrTe_3−xSe_x single crystals were grown by iodine vapor transport method.^[13,17] Two single crystals from different batches, both with nominal composition x = 0.04, were used for this study. Their exact compositions were determined by wavelength-dispersive spectroscopy (WDS), utilizing an electron probe microanalyzer (Shimadzu EPMA-1720). The dc magnetization was measured at H = 20 Oe, with zero-field cooling, using a SQUID (MPMS, Quantum Design). The samples were cleaved and cut to rectangular bars, with typical dimensions of 2.12 mm×1.01 mm×0.030 mm. The largest surface is ab-plane. The contacts were made directly on the sample surfaces with silver paint, which were used for both resistivity and thermal conductivity measurements. The contacts are metallic with typical resistance 200 mΩ at 2 K. The in-plane thermal conductivity was measured in a dilution refrigerator, using a standard four-wire steady-state method with two RuO₂ chip thermometers, calibrated in situ against a reference RuO₂ thermometer. Magnetic fields were applied along the c axis and perpendicular to the heat current. To ensure a homogeneous field distribution in the sample, all fields were applied at temperature above T_c.

According to the WDS results, the actual Se contents of the two ZrTe_3−xSe_x single crystals are x = 0.044 and 0.051, respectively. Below we will use the actual x. Figure 1(a) presents the normalized dc magnetization of ZrTe_2.956Se_0.044 and ZrTe_2.949Se_0.051 single crystals. The T_c defined by the onset of diamagnetic transition is 4.0 K for both samples. The significant diamagnetic response confirms that the superconductivity is stabilized to bulk from the filamentary superconductivity in pristine ZrTe₃, which is consistent with the previous report.^[17] This bulk superconductivity will be further supported by our thermal conductivity data in this study.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) The normalized dc magnetization of ZrTe2.956Se0.044 and ZrTe2.949Se0.051 single crystals, measured in H = 20 Oe with zero-field-cooled (ZFC) process. (b) The in-plane resistivity of ZrTe2.956Se0.044 and ZrTe2.949Se0.051 single crystals. No anomaly is observed in the normal state, suggesting the complete suppression of CDW state. (c) The resistive superconducting transition at low temperature. For clarity, the resistance of the x = 0.044 sample is magnified by five times. The Tc defined by ρ = 0 is 4.06 K and 3.87 K for x = 0.044 and 0.051 samples, respectively.

Figure 1(b) shows the in-plane resistivity ρ(T) of ZrTe_2.956Se_0.044 and ZrTe_2.949Se_0.051 single crystals. No anomaly is observed in the normal state, suggesting the complete suppression of CDW state in them.^[17] Fitting the normal-state resistivity data below 60 K to ρ(T) = ρ₀ + ATⁿ gives residual resistivity ρ₀ = 2.82 μΩ·cm and 21.5 μΩ·cm for the x = 0.044 and 0.051 samples, respectively. The resistive superconducting transition at low temperature is plotted in Fig. 1(c). The T_c defined by ρ = 0 is 4.06 K and 3.87 K for the x = 0.044 and 0.051 samples, respectively. Both of them are near the optimal doping in the phase diagram of ZrTe_3−xSe_x, and the x = 0.051 sample is slightly overdoped.^[17]

To determine their upper critical fields H_c2, the low-temperature resistivity of these two samples under magnetic fields was also measured. Figures 2(a) and 2(b) show the low temperature ρ(T) curves of ZrTe_2.956Se_0.044 and ZrTe_2.949Se_0.051 single crystals under various fields. With increasing field, the superconducting transition is gradually suppressed to lower temperature, and the magnetoresistance in the normal state is very weak. The H_c2(T), defined by ρ = 0 in Figs. 2(a) and 2(b), is plotted in Fig. 2(c) for both x = 0.044 and 0.051 samples. From Fig. 2(c), we roughly estimate H_c2(0) ≈ 1.40 T and 0.85 T for them, respectively.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Low-temperature resistivity of (a) ZrTe2.956Se0.044 and (b) ZrTe2.949Se0.051 single crystals under various magnetic fields. (c) Temperature dependence of the upper critical field Hc2(T) defined by ρ = 0 in panels (a) and (b). The dashed lines are guide to eye, which point to Hc2(0) ≈ 1.40 T and 0.85 T for x = 0.044 and 0.051 samples, respectively.

The temperature dependence of in-plane thermal conductivity for ZrTe_2.949Se_0.044 and ZrTe_2.956Se_0.051 single crystals in zero and applied magnetic fields is shown in Fig. 3, plotted as κ/T vs. T. The thermal conductivity at very low temperature can usually be fitted to κ/T = a + bT^α−1.^[19,20] The two terms aT and bT^α represent contributions from electrons and phonons, respectively. The power α is typically between 2 and 3 due to the specular reflections of phonons at the boundary.^[19,20] One can see that all the curves in Fig. 3 are roughly linear, therefore we fix α to 2. In zero field, the fittings give κ₀/T = 0.008 ± 0.008 mW·K⁻²·cm⁻¹ and 0.009 ± 0.002 mW·K⁻²·cm⁻¹ for the x = 0.044 and 0.051 samples, respectively. Such a tiny κ₀/T in zero field is negligible for both samples. As T → 0, since all electrons become Cooper pairs for the s-wave nodeless superconductors, there are no fermionic quasiparticles to conduct heat. Therefore there is no residual linear term of κ₀/T, as seen in V₃Si.^[19] However, for the unconventional superconductors with nodes in the superconducting gap, the nodal quasiparticles will contribute a finite κ₀/T in zero field.^[18] For example, κ₀/T = 1.41 mW·K⁻²·cm⁻¹ for the overdoped cuprate Tl₂Ba₂CuO_6+δ (Tl-2201), a d-wave superconductor with T_c = 15 K.^[21] For the p-wave superconductor Sr₂RuO₄, κ₀/T = 17 mW·K⁻²·cm⁻¹.^[22] Therefore, the negligible κ₀/T of the x = 0.044 and 0.051 samples suggests that the superconducting gap of ZrTe_3−xSe_x is nodeless. Note that the negligible κ₀/T in zero field also supports the bulk superconductivity in our samples.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Low-temperature in-plane thermal conductivity of (a) ZrTe2.956Se0.044 and (b) ZrTe2.949Se0.051 single crystals in zero and magnetic fields. The lines are fits of the data to κ/T = a + bTα−1, with α fixed to 2. The dashed lines represent the normal-state Wiedemann–Franz law expectations L0/ρ0 for the x = 0.044 and 0.051 samples, respectively.

When applying field, κ/T gradually increases with increasing field, as seen in Fig. 3. In H = 0.5 T, the fittings give κ₀/T = 8.27 ± 0.08 mW·K⁻²·cm⁻¹ and 1.14 ±0.03 mW·K⁻²·cm⁻¹ for the x = 0.044 and 0.051 samples, respectively. These values roughly meet their Wiedemann–Franz law expectations L₀/ρ₀ (L₀ is the Lorenz number 2.45 × 10⁻⁸ W·Ω·K⁻² and ρ₀ is the sample’s residual resistivity). The verification of the Wiedemann–Franz law in the normal state shows the reliability of our thermal conductivity measurements. The bulk H_c2(0) ≈ 0.5 T is taken for both samples, which is lower than those determined from the resistivity measurements.

To gain more information of the gap structure in ZrTe_2.956Se_0.044 and ZrTe_2.949Se_0.051, we check the field dependence of their κ₀/T. The normalized κ₀/T as a function of H/H_c2 is plotted in Fig. 4. For comparison, the data of the clean s-wave superconductor Nb,^[23] the multiband s-wave superconductor NbSe₂,^[24] and an overdoped sample of the d-wave superconductor Tl-2201 are also plotted.^[21] The slow field dependence of κ₀/T in low field for Nb manifests its single isotropic superconducting gap. In Fig. 4, the curves of the x = 0.044 and 0.051 samples are similar to that of NbSe₂, a multiband s-wave superconductor with the gap ratio Δ_l/Δ_s ≈ 3.^[24] This suggests that ZrTe_3−xSe_x also has multiple nodeless superconducting gaps. Previously, an ab initio calculation of the band structure for ZrTe₃ at ambient pressure gave a central rounded 2D Fermi surface sheet and two flatter q1D sheets.^[8] Therefore, the observation of multiple nodeless superconducting gaps in ZrTe_3−xSe_x system is not surprising.

Fig. 4.

	Figure Option ViewDownloadNew Window
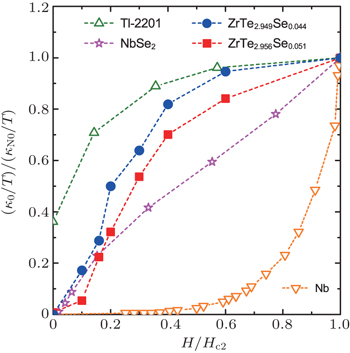	Fig. 4. Normalized residual linear term κ0/T of ZrTe2.956Se0.044 and ZrTe2.949Se0.051 single crystals as a function of H/Hc2. Similar data of the clean s-wave superconductor Nb,[23] an overdoped d-wave cuprate superconductor Tl-2201,[21] and the multiband s-wave superconductor NbSe2[24] are also plotted for comparison.

Theoretically, it has been shown that unconventional superconductivity with d_xy symmetry can appear in close proximity to a charge-ordered phase, and the superconductivity is mediated by charge fluctuations.^[25,26] Since the d_xy-wave gap has line nodes, our results clear rule out this kind of unconventional superconductivity in ZrTe_3−xSe_x. In this context, the superconductivity in ZrTe_3−xSe_x is likely conventional. Similar situation happens in the Cu_xTiSe₂ system. Thermal conductivity measurements suggested conventional s-wave superconductivity with a single isotropic gap in Cu_0.06TiSe₂, near where the CDW order vanishes.^[27] So far, the evidence for unconventional superconductivity induced by CDW fluctuations in real materials is still lack. The experiments on more systems with superconductivity near a CDW QCP are needed.

In summary, we have measured the ultra-low-temperature thermal conductivity of ZrTe_2.956Se_0.044 and ZrTe_2.949Se_0.051 single crystals, which are near the optimal doping in the phase diagram of the ZrTe_3−xSe_x system. The absence of κ₀/T in zero field for both compounds gives strong evidence for nodeless superconducting gap. The field dependence of κ₀(H)/T further suggests multiple nodeless gaps in ZrTe_3−xSe_x. Unconventional superconductivity with line nodes is excluded in this trichalcogenide system although there is a CDW QCP. It is likely that the superconductivity in ZrTe_3−xSe_x is still conventional.