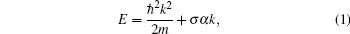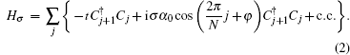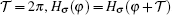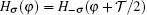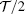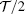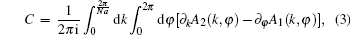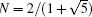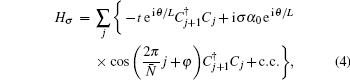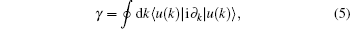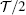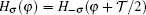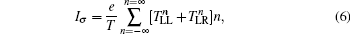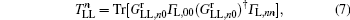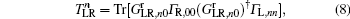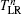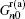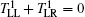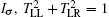1. IntroductionSince the first prediction and the subsequent experimental confirmation, the field of topological insulators[1–6] has seen an explosion of research interests in both experimental and theoretical aspects. The topological states of matter are classified according to the topological invariants which are the intrinsic properties of Bloch energy bands, and thus different topological states are characterized by different topological indices. When a system with a given topological index is continuously deformed into a system with a different index, the bulk energy gap must close so that a topological quantum phase transition can occur. In real space, a conductive boundary (interface) state appears to bridge the two different topological phases and is described by the massless Dirac equation. If a system can be deformed continuously to another system without closure of the bulk energy gap, the two systems should have the same topological invariants.
Classification and identification of different topological phases are one of the central issues in the topological insulator field. Recently, much attention has been paid to exploring the topological phases in the one-dimensional (1D) optical superlattice systems,[7–15] ultracold atom boson systems,[16,17] and 1D topological superconductors.[18–24] In particular, when the topological states characterized by the bound states have been experimentally confirmed by using optical waveguides,[9,10] the research on 1D topological systems has been further intensified. For these 1D quasiperiodic systems, such as the Harper model[25] (or Aubry–André model[26]) and the Fibonacci quasicrystal,[27] the common point of the topological phases is the spatial quasiperiodic modulation (QPM) of the site energy (diagonal term) or the hopping energy (off-diagonal term) of particles in the tight-binding representation. Certainly, these two types of QPMs are topologically equivalent,[7] because they can be transformed into each other without closing the bulk energy gap. These 1D QPM systems are somewhat similar to the SSH model[28,29] used originally to explain the dimerization and trimerization of polyacetylene, but the physics behind them is different depending on the concrete symmetries of the systems.
It is observed that the topological phase in the 1D QPM systems comes from the modulation of the hopping-energy magnitude of particles (the site-energy QPM is topologically equivalent[7]), and little attention has been paid to QPM of the hopping phase. This motivates us to study the possible 1D topological phase, which mainly results from the hopping-phase modulation. A 1D semiconductor wire with an oscillating Rashba spin–orbit coupling (RSOC) can meet such a requirement as a realistic model. On one hand, electrons in the wire have a spin-dependent hopping phase[30] (Aharonov–Casher phase) due to the spin precession from RSOC, and thus the modulation of the RSOC strength in turn changes the hopping phase of the electrons.[31] On the other hand, the RSOC strength can be controlled by an external electric field[32] and a spatially oscillating RSOC wire can be fabricated in principle. We show that a pair of particle–hole symmetry energy gaps appear in the energy band due to the oscillating RSOC, and fractional boundary states reside at the ends of the wire transversing the bulk energy gap. These states can be characterized by a quantized Berry phase ±π. Besides, a quantized charge 2e can be pumped out in a pumping cycle because of the spin-flipping effect when the RSOC is varying slowly with time.
2. ModelThe RSOC comes from the relativistic effect[33] and is much larger in semiconductor materials such as InAs. The RSOC strength is dependent on an internal electric field of the asymmetric potential (Ez = ∂U(z)/∂z) confining a 2D quantum well plane. In a continuum model, the RSOC wire reads H = p2/2m + (α(Ez)/ħ)(σ × p)z, with the RSOC strength α, the electron spin operator σ, the momentum operator p, and the electron mass m. α(Ez) has already been demonstrated in experiment to vary with an external electric field.[32] For a noninteracting 1D Rashba wire and the spin quantum axis set along the Rashba vector, the energy dispersion is simply given by
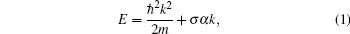
where
σ = ± denotes the spin direction of the Rashba wire. When a spin not along the Rahsba vector enters the Rashba wire, it will be rotated and the spin flip or precession phase is given by
αmL/
ħ2 with
L being the wire or the precession-path length. Therefore, the RSOC is generally believed to modulate the spin-dependent phase of electron hopping but not the electron transmission.
[34]After discretizing the continuum model above, we can obtain the following spin-dependent tight-binding version of the noninteracting Rashba wire:
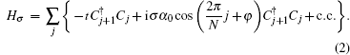
Here the first term describes the energy band of a free-electron wire, and the second one is the discretized RSOC term. A spatially oscillating RSOC strength is considered.  is the electron creation (annihilation) operator at site j, and σ = ± 1 = ↑↓ is the spin index. In the second term, α0 = α/2a is the lattice version of the RSOC strength with the lattice constant a. Here we consider the RSOC oscillating in space by adding a cosine term, φ is assumed to be a modulated phase, and when N is an integer, the wire has a superlattice structure with the periodic length Na. As a result, the unit cell of the superlattice wire is enlarged by N fold, while the first Brillouin zone is reduced to [−π/(Na), π/(Na)] from the original one [−π/a, π/a]. When N is an irrational number, the RSOC modulation is incommensurate with the wire lattice and the system is quasiperiodic.
is the electron creation (annihilation) operator at site j, and σ = ± 1 = ↑↓ is the spin index. In the second term, α0 = α/2a is the lattice version of the RSOC strength with the lattice constant a. Here we consider the RSOC oscillating in space by adding a cosine term, φ is assumed to be a modulated phase, and when N is an integer, the wire has a superlattice structure with the periodic length Na. As a result, the unit cell of the superlattice wire is enlarged by N fold, while the first Brillouin zone is reduced to [−π/(Na), π/(Na)] from the original one [−π/a, π/a]. When N is an irrational number, the RSOC modulation is incommensurate with the wire lattice and the system is quasiperiodic.
Since the 1D case is focused on, the spin space (σ) is diagonal, which comes from the fact that the quantum spin axis is chosen along the Rashba vector. In other words, the following results that we obtain from Hσ of Eq. (2) are also applicable for the spin-opposite Hamiltonian H−σ. The oscillating periodicity of Hσ upon φ is 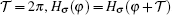 . Nevertheless, one can see
. Nevertheless, one can see 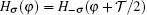 , and thus the whole Hamiltonian H = ∑σHσ has a reduced oscillating periodicity
, and thus the whole Hamiltonian H = ∑σHσ has a reduced oscillating periodicity 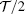 . Actually, when φ varies from φ = 0 to φ =
. Actually, when φ varies from φ = 0 to φ = 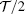 , both σ and −σ spins experience a flipping process and the whole system is unchanged. Alternatively speaking, the variation of RSOC can produce an accumulated spin-flip phase, which is exactly the acquired phase of electrons moving in the RSOC medium.[31] In the following discussion, we focus on results from Hσ to study the possible topology of the 1D Rashba wire while H−σ is not taken into account because of exact spin degeneracy.
, both σ and −σ spins experience a flipping process and the whole system is unchanged. Alternatively speaking, the variation of RSOC can produce an accumulated spin-flip phase, which is exactly the acquired phase of electrons moving in the RSOC medium.[31] In the following discussion, we focus on results from Hσ to study the possible topology of the 1D Rashba wire while H−σ is not taken into account because of exact spin degeneracy.
We first consider a superlattice structure of the RSOC wire by assuming an integer N, the original single energy band with a constant RSOC, E = −2t coska + 2α0σ sinka, will split into N subbands and there should be some transparent energy gaps between neighboring subbands. In Fig. 1, we plot the energy band of the wire in the folded Brillouin zone with different periods N. t = 1 is set as the energy unit in our calculations and the RSOC strength is taken as α0 = 0.5t. It is seen that there are only two transparent bulk energy gaps related by the particle–hole symmetry, and other theoretical energy gaps between subbands are hardly seen. This is different from the usual 1D superlattice systems with modulation to the hopping-energy or site-energy of electrons,[10–12] in which there are almost N−1 energy gaps with nearly equal magnitude. It should come from the periodic modulation to the electron's hopping phase in the studied case, because such a phase modulation (spin-flip accumulated phase) has lesser influence on the energy dispersion in comparison to the site-energy or hopping-energy modulation. The only two transparent gaps are therefore characteristic for the periodic modulation to the electron's phase. It is shown in Fig. 1 that the energy band E(k) of the oscillating RSOC wire is almost independent of the phase φ since the lines are not broadened due to different φ. This reflects that the energy band is not crucially dependent on the variation of the hopping phase. The lower (higher) energy gap locates between the second and the third lowest (highest) subbands. When the Fermi energy resides in the gap and the filling factor of the system is ν = 2/N or ν = (N−2)/N, the periodic superlattice RSOC wire shall be an insulator.
3. Topological numberIn order to judge whether the 1D Rashba wire with the energy band in Fig. 1 enters into a topological state or not, we need first to calculate the Chern number of Hσ. The Chern number is defined as[35–37]
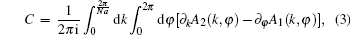
where
A1(2) = ⟨
u(
k,
φ)|
∂k(φ)|
u(
k,
φ)⟩ is the Berry connection, |
u(
k,
φ)⟩ is the Bloch function of the system,
Hσ|
u(
k,
φ)⟩ =
E(
k,
φ)|
u(
k,
φ)⟩. The energy dispersion in this 1D system is also periodic over the parameter
φ besides the momentum
k, and moreover, the system keeps insulating with variation of
φ, so one can have the above Chern-number definition of the 1D system through the dimension extension. The calculated results of each subband are marked in Fig.
1. It is seen that the Chern number is nonzero and equals
C = ∓ 2 when the filling factor is 2/
N ((
N−2)/
N). The nonzero Chern number also means that the system can pump out adiabatically a quantized charge in a pumping cycle when the periodic parameters (
φ) are time-dependent. However, for the studied case, the pumped charge number should be 2 not 1, the latter is the case of those 1D topological systems
[7,8,9] with Chern number
C = ± 1.
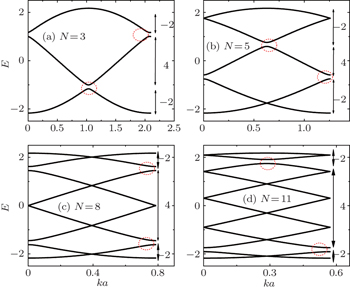
For a topological phase, there often exist topologically protected gap-transversing boundary states in a finite-size system. We now consider a finite-length NTa Rashba wire, where NT is the total number of lattice sites in the system, the energy band is calculated with an open boundary condition and the numerical results are shown in Fig. 2. It is seen that two curves transverse the bulk gap opened by the oscillating RSOC in Figs. 2(a) and 2(b). Here only the lower band gap is plotted, in fact, the higher energy gap has the same situation. Similarly, although only the N = 3 case is presented, all other cases are the same except for N = 4, in which the gap locates at the particle–hole symmetry point of the system, so that a flat-band forms and the system is no longer insulating.
It is shown in Fig. 2(a) that there are two crossing points (Dirac points) in the energy gap at φ = 0 and φ = π, and they correspond to the inversion symmetry that the wire possesses even with the additional RSOC modulation, as is seen from the renormalized hopping energy t̃ in a supercell,[10] which fulfills t̃N−j = ±t̃j in Eq. (2). The distributions of several selected wave functions ψA,B,C,D in the energy gap are plotted in Fig. 2(c), and they are the same and localize symmetrically at the two ends of the wire, referred to as the charge-1/2 fractional boundary state.[18,19] In fact, these fractional boundary states are a manifestation of the topologically nontrivial phase of the system, and thus are protected by the inversion symmetry of the wire. When such symmetry is absent, e.g., the remainder of NT/N is nonzero, the fractionary boundary states vanish, and the boundary states reside only at one end of the wire depending on the parameter φ. The bulk–edge correspondence is shown in Fig. 2(b) while the wave functions are presented in Figs. 2(d) and 2(e). Here the boundary states transversing the gap, although depending on the specific phase φ, shall be a manifestation of the topological phase.
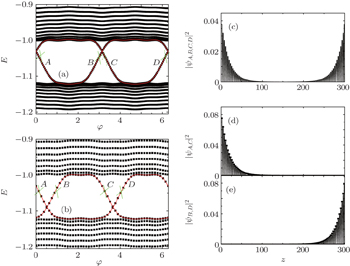
For the above superlattice RSOC wire, whether the modulation to the electron phase can lead to a topological phase is relying on a specific φ or the wire length due to the lack of spacial ergodicity. We shall consider a quasiperiodic Rashba wire with an irrational number N (Eq. (2)), taking 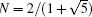 as an example. Similarly, there are two particle–hole symmetry bulk energy gaps in a finite-size wire and two boundary states appear in each gap. In Fig. 3(a), we show the lower energy gap as a function of φ as well as the gap-transversing states in the finite-length wire, it is nearly the same as that of the periodic case N = 3 in Fig. 2(a), but the typical boundary states are different as shown in Figs. 3(b) and 3(c). Obviously, the fractional boundary states vanish due to the absence of the inversion symmetry, instead, the one-end states emerge. These end states indicate that the QPM-structure wire turns into a topologically nontrivial phase, which can be indexed by a nonzero Chern number of a ring system.[7] Since the QPM wire is not periodic and one cannot calculate the Chern number according to Eq. (3), the finite-size QPM wire with length L is considered to constitute a ring and form an infinite periodic system. Meanwhile, a twisted phase θ is introduced into the system's Hamiltonian as
as an example. Similarly, there are two particle–hole symmetry bulk energy gaps in a finite-size wire and two boundary states appear in each gap. In Fig. 3(a), we show the lower energy gap as a function of φ as well as the gap-transversing states in the finite-length wire, it is nearly the same as that of the periodic case N = 3 in Fig. 2(a), but the typical boundary states are different as shown in Figs. 3(b) and 3(c). Obviously, the fractional boundary states vanish due to the absence of the inversion symmetry, instead, the one-end states emerge. These end states indicate that the QPM-structure wire turns into a topologically nontrivial phase, which can be indexed by a nonzero Chern number of a ring system.[7] Since the QPM wire is not periodic and one cannot calculate the Chern number according to Eq. (3), the finite-size QPM wire with length L is considered to constitute a ring and form an infinite periodic system. Meanwhile, a twisted phase θ is introduced into the system's Hamiltonian as
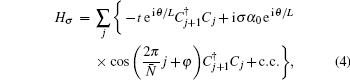
with
N̅ = [
N·
L]/
L. Note that the hopping modification due to
θ should also go to the RSOC term and at the limit of
θ = 0,
L→∞, so that equation (
4) can coincide with the QPM wire Hamiltonian. By scanning
θ and
φ, we can calculate the Chern number by replacing
k with
θ in Eq. (
3), since
Hσ(
θ,
φ) =
Hσ(
θ + 2
π,
φ + 2
π). In this ring structure, we set
L = 300
a and obtain the same Chern structure as those in Fig.
1, i.e., the lower insulating band has a nonzero Chern number
C = −2. Therefore, the boundary states in Fig.
3 should also manifest the topological phase of the oscillating RSOC wire.
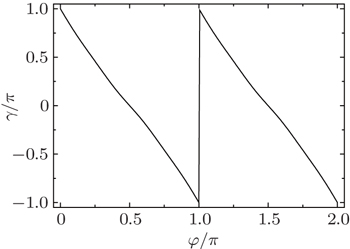
4. Berry phaseWe proceed to calculate the Berry phase of the Rashba 1D wire to further discern the fractional boundary states in Fig. 2(c). The Berry phase is defined as[36,37]
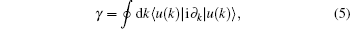
where
u(
k) is the Bloch wave function in the folded Brillioun zone and all states below the Fermi energy should be summed. The results are presented in Fig.
4 and the Berry phase is quantized
γ/
π = ± 1 at
φ = 0 and
φ =
π. This quantization is also a hallmark of the topological phase in the 1D system. The fractional bound states
ψA,C and
ψB,D in Fig.
2(a) should have the opposite chiralities,
∂ E/
∂φ. However, the distributions of all 4 wave functions in real space shown in Fig.
2(c) are entirely the same. This is also manifested in Fig.
4 that for the
A(
C) and
B(
D) points, the Berry phases are opposite. Actually, this chirality represents the spin-flip direction. When
γ = 0 in Fig.
4 or
φ =
π/2 in Fig.
2(a), the system is in a topologically trivial state and the original fractional boundary states at
φ = 0 are evolved into the insulating bulk states. In other words, the system exhibits an alternation of the topologically nontrivial and trivial states with an adiabatic variation of
φ but keeps insulating, and thus, a quantized charge should be pumped out of the system.
The results in Figs. 2–4 oscillate with φ and the periodicity seems to be 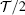 , however, the Hamiltonian Hσ we used as well as its eigenfunction should have a clear periodicity of T. As discussed earlier, the RSOC can generate a spin flip (precession) phase, but the system remains spin-unpolarized, so
, however, the Hamiltonian Hσ we used as well as its eigenfunction should have a clear periodicity of T. As discussed earlier, the RSOC can generate a spin flip (precession) phase, but the system remains spin-unpolarized, so 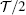 is the spin-flipped periodicity as seen from
is the spin-flipped periodicity as seen from 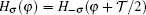 . Alternatively, Hσ and H−σ have the same eigenvalue but the wave functions have a π phase shift. When φ > π in Figs. 2–4, the spin can be considered to flip from σ into -σ, i.e., the wave functions, ψC and ψD, represent the opposite spin eigenfunctions with respect to ψA and ψB. Moreover, ψB and ψC are degenerate at φ = π but with opposite chiralities, while ψA and ψD are degenerate at φ = 0. Therefore, the two points φ = 0 or φ = π are the critical spin-flip points.
. Alternatively, Hσ and H−σ have the same eigenvalue but the wave functions have a π phase shift. When φ > π in Figs. 2–4, the spin can be considered to flip from σ into -σ, i.e., the wave functions, ψC and ψD, represent the opposite spin eigenfunctions with respect to ψA and ψB. Moreover, ψB and ψC are degenerate at φ = π but with opposite chiralities, while ψA and ψD are degenerate at φ = 0. Therefore, the two points φ = 0 or φ = π are the critical spin-flip points.
5. Pumped currentAccording to Thouless's argument,[38] a topological insulator can pump out a quantized number of charges in a pumping cycle that equals the Chern number for the filled band.[39,40] In the following, we calculate the pumped current in a two-terminal device to demonstrate this equality. The device is the 1D Rashba wire sandwiched by two normal metals that are absent of the time-dependent RSOC. Here we assume that the parameter φ is adiabatically varying, and φ in Eq. (2) is replaced by ϖt with the pumping frequency ϖ and time variable t. In the adiabatic limit, the frequency is considered to be infinitely small ϖ → 0. With the help of Floquet theory and nonequilibrium Green's function method, the pumped current (derivations are shown in Appendix A) flowing in the left electrode is given by
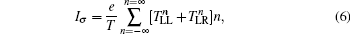
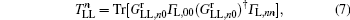
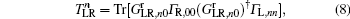
where
e is the electron charge and
T = 2
π/
ϖ is the pumping periodicity.

represents the scattering coefficient of electrons that inject into the device from the left lead (L) and exit out of the left lead (L) again by absorbing/emitting
n photons in the wire device, and
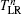
is for electrons going from the right lead (R) to the left one (L) through the device, where the electrons similarly absorb or emit
n photons.
ΓL(R),nn denotes the line-width function matrix of the left (right) lead with an energy shift of
nħϖ,
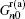
is the delayed (advanced) Green's function of the system with the same energy shifts
nħϖ that are due to emission or absorption of photons in the pumping process. The zero-photon process does not contribute to the pumped current here. Usually, the multiphoton process has an exponentially smaller contribution to the pumped current than the single-photon process, especially for adiabatic pumping and weak time-dependent term.
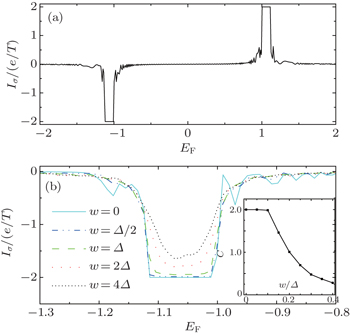
The pumped current Iσ is presented as a function of the Fermi energy EF in Fig. 5(a). We can see that Iσ is quantized as Iσ = 2e/t when EF is residing in the energy gap of the wire, and the current direction is reversed for the two gaps. This is exactly consistent with Thouless's argument, the pumped charge number is quantized and equal to the Chern number C = ±2 of the filled bands as shown in Fig. 1, although we have calculated the current in a finite-length wire. It is noted that the wire length should be much longer than the damping length of the boundary states in order to suppress the excitation of the boundary states from the finite-size effect, and the quantized pumping remains unchanged irrespective of the rational or irrational number N taking in the calculations. When EF transverses the bulk band not in the energy gap, the wire is conductive and the pumped current is negligibly small in comparison to the quantized current. This can be understood from the Brouwer's pumping formula[41] that the pumped current depends on the parametric derivatives of the S-matrix elements. In the studied 1D wire case, there exist multi-pumping resources (parameters) since all hopping terms are time-dependent, which must result in randomization of the accumulated Berry phases during the cyclic evolution, so the pumped current is negligibly small.
In our calculations, the single-photon process is actually prohibited, 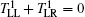 , and only the two-photon process contributes to
, and only the two-photon process contributes to 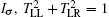 . This confirms the earlier analysis that in a pumping cycle, spin-σ electrons entering into the device from the L or R electrode will experience spin-flip twice to return to the original state. In other words, the single-photon process leads to a spin-flipped state that is an intermediate excited state not the eigenstate of the system, so this scattering process is prohibited; whereas the two-photon process leads to spin-flip twice so that the final state is in the same spin state as (not orthogonal to) the initial state, so this process is allowed and the charge can be pumped out. Electrons entering the device from one lead will change their energy ± 2ħϖ driven by the pumping resources, and flow to the other lead with a unit transmission, thus the pumped current is Iσ = 2e/T. In the real space, with the help of the boundary wave functions in Figs. 2(d) and 2(e), the pumping process is clear. At time t = 0+ or (φ = 0+), a spin-σ electron (ψA) locates at the left end of the wire, it then evolves to the right end state ψB at t = T−/2 (φ = π−), so the system transports this electron through the wire. At the next moment t = T+/2 (φ = π+), the system is in the spin (−σ) state ψC. The same process repeats and the spin state will reverse by pumping out an electron. Therefore, two charges in a pumping periodicity are pumped out due to the spin-flip effect from the RSOC in a pumping cycle.
. This confirms the earlier analysis that in a pumping cycle, spin-σ electrons entering into the device from the L or R electrode will experience spin-flip twice to return to the original state. In other words, the single-photon process leads to a spin-flipped state that is an intermediate excited state not the eigenstate of the system, so this scattering process is prohibited; whereas the two-photon process leads to spin-flip twice so that the final state is in the same spin state as (not orthogonal to) the initial state, so this process is allowed and the charge can be pumped out. Electrons entering the device from one lead will change their energy ± 2ħϖ driven by the pumping resources, and flow to the other lead with a unit transmission, thus the pumped current is Iσ = 2e/T. In the real space, with the help of the boundary wave functions in Figs. 2(d) and 2(e), the pumping process is clear. At time t = 0+ or (φ = 0+), a spin-σ electron (ψA) locates at the left end of the wire, it then evolves to the right end state ψB at t = T−/2 (φ = π−), so the system transports this electron through the wire. At the next moment t = T+/2 (φ = π+), the system is in the spin (−σ) state ψC. The same process repeats and the spin state will reverse by pumping out an electron. Therefore, two charges in a pumping periodicity are pumped out due to the spin-flip effect from the RSOC in a pumping cycle.
We proceed to examine the disorder effect on the topological phase. Here we focus on the onsite-energy disorder that is chosen in the range [−w/2, + w/2] with the random disorder strength w, and the results are averaged over 400 sample configurations. First, we find that the fractional boundary states in Fig. 2(c) would be seriously destroyed when a single disorder configuration is considered, and they are transformed into either the left end state in Fig. 2(d) or the right one in Fig. 2(e). However, when we carry out the disorder configuration average, the fractional boundary states will be recovered. This further demonstrates that the fractional boundary states stem from the inversion symmetry. In Fig. 5(b), we plot the pumped current as a function of energy with different disorders. It is shown that the quantized current Iσ is hardly affected as long as the energy gap (Δ) is larger than the disorder strength, Δ > w, where Δ ≃ 0.1t in the wire. This agrees with the fact the quantization of the pumped current as a hallmark of the topological state is protected by the topology of the wire. When w > Δ in Fig. 5(b), the quantization of Iσ as well as the Chern number (shown in the inset of Fig. 5(b) are severely destroyed. In other words, if any excitation due to disorder, finite temperature, finite pumping frequency, or electron–electron interaction, cannot close the energy gap, the topological invariant will be well-defined and thus the quantized pump should persist.
6. ConclusionWe have investigated the possible topological phase in an oscillating RSOC quantum wire by considering periodic or quasiperiodic modulation to the hopping phase of electrons. It was found that a pair of particle–hole-symmetry energy gaps occur in the original energy band and the system has a nonzero Chern number through dimension extension. As the 1D Rashba wire has the inversion symmetry, fractional boundary states are found to reside in the gap and characterized by the quantized Berry phase ±π. We demonstrated that when the RSOC varies slowly with time, the system can pump out 2 quantized charges in a pumping cycle due to the spin-flip effect. The quantized pumping is topologically protected and robust against moderate disorders. Our findings provide a new way to design a 1D topological phase by modulating the electron hopping phase.