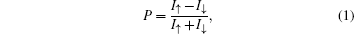Spin resonance transport properties of a single Au atom in S–Au–S junction and Au–Au–Au junction
Department of Physics, Tsinghua University, Beijing 100084, China
† Corresponding author. E-mail: ligqin@mail.tsinghua.edu.cn
Project supported by the National Basic Research Program of China (Grants No. 2011CB921602) and the National Natural Science Foundation of China (Grants No. 20121318158).
1. IntroductionMolecular electronics is an important area underpinning the future of the electronic and the information technology industry. [1–13] Among the many molecules proposed in molecular electronics, single-molecular magnets (SMMs) appear as particularly attractive. In general, they show both classical and quantum properties, such as magnetization hysteresis, quantum coherence, spin tunneling of the magnetization, and quantum phase interference.[14–19] When such molecules are inserted into a device where a current flows, then the exchange interaction between the itinerant electrons and the SMMs can be used to write in and read out information,[20–23] namely it can be used to realize molecular electronics with spins, i.e., molecular spintronics.[24,25] Importantly, the typical length scale of these SMM junctions is rather close to that of materials used to perform quantum information processing with nuclear magnetic resonance (NMR)[26–28] or electron spin-resonance (ESR).[29] As such, the combination of molecular electronics and SMMs by means of electrical nano-junctions incorporating SMMs, may provide an ideal material platform for implementing both classical and quantum logic circuits.[30]
In this paper, we want to investigate the spin transmission properties of a single Au atom connected to two Au nanowires. Since the electron spin of the single Au atom can be operated by transmission spin current or a specified frequency laser, this kind of single atom junction may be a candidate to perform quantum information processing. The single Au atom is fixed on a point by laser with a specified spin +1/2 and the two Au nanowires can move as a whole along their extending direction respectively. The transport properties of our junctions certainly should depend on the distance between anchor atoms and the single Au atom, and this distance can be set to different values. The widening of the distance can break the chemical bonding between the anchor atom and the single Au atom, and redistribute the spin state of the single Au atom.
We perform a first-principles theoretical investigation on the spin properties of S–Au–S junction and Au–Au–Au junction using the smeagol code,[31–33] which combines density functional theory (DFT) with first-principles nonequilibrium Green function (NEGF). The unique properties such as high spin polarization, stability of spin state, Fermi energy drift and bias-dependent spin filtering will be shown, and the importance of orbital energy shift between anchor atoms and the center Au atom will be discussed in this paper.
2. Transmission property of S–Au–S junctionTo study the transport properties of a single Au atom with a specified spin direction, we create an ideal model in an electronic circuit: a single Au atom is connected to two quasi-one-dimensional Au nanowires by two S atoms (Fig. 1). The distance between two Au atoms in the electrode bulk is 2.884 Å, which is typically the Au–Au bond length in a gold metal lattice, and the distance between a S atom and its nearest three electrode Au atoms is 2.526 Å. The distance between the S atom and the center Au atom will be set to different values during our study.
Figure 2 shows the I–V curves (Figs. 2(a)–2(c)) and spin polarization (Fig. 2(d)) of S–Au–S junction. Comparing spin-up current (Fig. 2(a)) and spin-down current (Fig. 2(b)), we can see the difference between them as the distance between the S atom and the center Au atom increases. This is rather obvious if we focus on the spin polarization at bias of 0.3 V, as shown in Fig. 2(d). Here, the spin polarization P is defined as
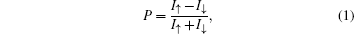
where
I↑ is the spin-up current and
I↓ is the spin-down current. We can see a sudden rise of spin polarization
P from 3.2 Å to 3.5 Å. When the distance between the S atom and the center Au atom is shorter than 3.2 Å, spin-up current and spin-down current increase together with the same slope, and the total current follows their growing trend. When the distance is longer than 3.5 Å, the spin-up current is much larger than the spin-down current, and the total current is mainly affected by its spin-up part. Just at the distance of 3.5 Å, in Fig.
2(a) the increasing trend of black line (3.5 Å) is quite different from that of blue line (3.2 Å), while in Fig.
2(b) the black line follows the same increasing trend of the blue line, indicating that the +1/2 spin of the center Au atom only influences the spin-up current.
According to the projected density of state (PDOS) of the center Au atom in a S–Au–S junction (Figs. 2(e)–2(g)), the spin-up peak −6.033 eV and the spin-down peak −6.023 eV are very close at the distance of 3.2 Å. when the distance increases, the spin-up peak rises and moves to the left side, while the spin-down peak falls and moves to the right side. Finally, at the distance of 3.8 Å, the spin-up peak rises to a rather high level, but the spin-down peak is almost disappeared in the graphic scales. According to this PDOS analysis, it is clear that the S–Au ionic bond breaks at the distance of about 3.5 Å, and this process will redistribute the spin state of the center Au atom.
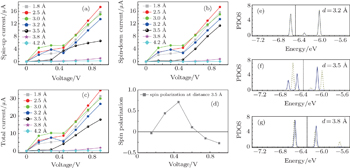
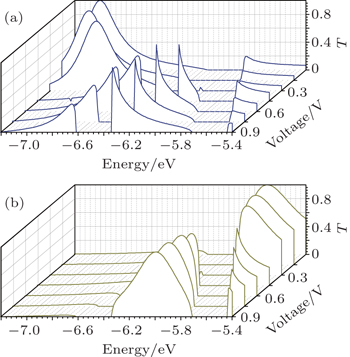
Comparing this PDOS distribution with the transmission coefficients (Fig. 3), we can better understand the spin current divergence.
Figures 3(a) and 3(b) show the transmission coefficients of spin-up and spin-down electrons at the distance of 3.5 Å at different biases. The several high peaks in Fig. 3(a) and the only single peak in Fig. 3(b) form a sharp contrast. Spin-up itinerant electrons have a large transmission probability in most energy regions, while spin-down electrons can only transport through the junction with energy from −6.35 eV to −5.71 eV. Compared with the PDOS of the center Au atom in Fig. 2(f), the transmission coefficient valley of spin-up itinerant electrons in Fig. 3(a) is related to the spin-up PDOS peak −6.26 eV (solid line), indicating that spin resonance can transport spin-up itinerant electrons with similar energy, except the valence orbital is already occupied by the +1/2 electron. While the single spin-down transmission peak in Fig. 3(b) is related to the spin-down PDOS peak −5.90 eV (dot line) in Fig. 2(f), or rather this spin-down transmission peak is related to the valence orbitals of anchor S atoms. Note that the single spin-down transmission peak rising represents that the spin-down itinerant electrons have an increasing probability to transport from one S atom to the other as the bias is rising. The above transmission coefficient analysis is consistent with the sudden curve rising of spin polarization P in Fig. 2(d). Since the spin current is calculated as the integral of the transmission coefficient and Fermi distribution while the Fermi distributions of spin-up and spin-down itinerant electrons are exactly the same at a certain bias, the significant current divergence is attributed to the huge transmission probability difference.
Figures 3(c) and 3(d) show the transmission coefficients of spin-up and spin-down electrons at different distances at a bias of 0.3 V. When the distance is shorter than 3.2 Å, transmission coefficients of spin-up and spin-down electrons are quite the same. This is because the chemical bond between the S atom and the center Au atom shares their electrons, the valence orbital of the center Au atom contain both spin electrons. Even we specify the electron spin of the center Au atom as +1/2 at the beginning, the final electron distributions of spin-up and spin-down electron in its valence orbital are exactly the same. This symmetry of spin electron distributions makes the transmission coefficients as well as the integral of spin current all the same. Just at the distance of 3.5 Å (cyan line), the spin-up PDOS peak −6.264 eV corresponds to a wide transmission coefficient peak, which means that the spin-up itinerant electrons can transport easily by the spin resonance with the center Au atom. The spin-down PDOS peak −5.903 eV corresponds to a broadening transmission peak, suggesting that the spin-down itinerant electrons can only tunnel directly between two anchor S atoms. In this case, the spin-up electrons around Fermi energy (−6.4 eV) have a great possibility to transport from one electrode to the other, while the spin-down electrons are almost forbidden to pass through. When distance is larger than 3.5 Å, we can see that the main spin-up transmission peak becomes narrower and the spin-down transmission peaks gradually disappear. Thus spin-up itinerant electrons with energy about −6.6 eV can still transport easily by the spin resonance mechanism, while it is too difficult for the tunnelling of spin-down itinerant electrons to occur due to the large distance.
3. Transmission property of Au–Au–Au junctionIn order to make the transmission mechanism more clear, we perform the same NEGF and DFT calculation to an Au–Au–Au junction. Referring to the structure shown in Fig. 1, we change those two yellow balls to Au atoms and keep the other initial parameters all the same including the spin +1/2 of the center Au atom.
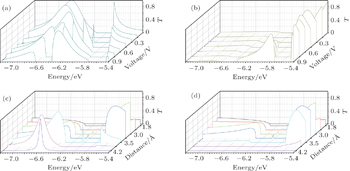
The spin currents of the Au–Au–Au junction in different distances are shown in Fig. 4. In most cases, the spin polarization is not as large as the one in the S–Au–S junction, except at the distance of 3.5 Å (black line). The black line in Fig. 4(a) rises rapidly from bias 0.30 V to 0.45 V, but slows its trend soon. While the black line in Fig. 4(b) begins to rise after bias 0.45 V, and keeps its slope till the final bias. So the spin polarization P of the Au–Au–Au junction at the distance of 3.5 Å (Fig. 4(d)) changes from positive to negative when bias increases. Figures 4(e)–4(g) show the PDOS of the center Au atom at bias 0.9 eV. A significant difference between PDOSs of S–Au–S junction and Au–Au–Au junction is the distance dependence of Fermi energy (the vertical dash lines). In the S–Au–S junction Fermi energy of the scattering region is stable at about −6.40 eV at various distances, while in the Au–Au–Au junction Fermi energy drifts from −6.501 eV at the distance of 1.8 Å to −6.214 eV at the distance of 4.2 Å. Distance increasing causes the rupture of Au–Au metallic bonds, and the connected nano Au wire breaks into two semi-infinite electrodes. Because of this restructure process, Fermi energy of the Au–Au–Au scattering region increases. For the S–Au–S junction, anchor S atoms separate two semi-finite Au electrodes in the beginning, the rupture process only greatly affects the bond between the S atom and the center Au atom, but affects little the bond between the S atom and the electrode Au atoms. So Fermi energy of the S–Au–S junction keeps stable during the rupture process.
The spin-up and spin-down electron distributions of the Au–Au–Au junction are almost the same at the distance of 3.2 Å and 3.8 Å, while at the distance of 3.5 Å, spin-up peak −6.5 eV and spin-down peak −6.03 eV split into two peaks respectively. The special peak splitting at the distance of 3.5 Å indicates the rupture of Au–Au metallic bond, which coincides with the same rupture distance in the S–Au–S junction. Because of this PDOS peak splitting, the spin-up coefficient transmission valley (Fig. 5(a)) has a sharper edge and the spin-down transmission coefficient peak (Fig. 5(b)) has a larger width at half maximum.
For spin-up electrons (Fig. 5(a)), transmission coefficients form a valley below Fermi energy −6.30 eV, which is related to the −6.5 eV PDOS peak splitting of spin-up electron in Fig. 4(f). For spin-down electrons (Fig. 5(b)), transmission coefficients form a peak above Fermi energy, which can also be related to the PDOS peak −6.03 eV splitting of spin-down electron in Fig. 4(f). It means that at the distance of 3.5 Å, PDOS peak splitting of spin-up electron causes a forbidden effect, while the PDOS peak splitting of spin-down electron leads to a conduction effect. These two effects determine the large difference between spin-up and spin-down current. As bias increases from zero, the right side of the spin-up valley first comes into a bias window and enlarges the spin-up current, but soon the bottom part comes into the bias window and the spin-up current slows increasing. For spin-down electrons, the wide transmission peak comes into the bias window latter but keeps the spin-down current increasing with the same rate. Thus the corresponding spin polarization value at the distance of 3.5 Å switches from positive to negative as shown in Fig. 4(d).
Compared with the transmission coefficients of the S–Au–S junction at the distance of 3.5 Å (Figs. 3(a) and 3(b)), the spin-up transmission valley [−6.60, − 6.36] eV forms sharper edges (Fig. 5(a)) and the main spin-down transmission peak −6.0 eV is higher and wider (Fig. 5(b)). These two differences can also be attributed to the PDOS peak splitting of the Au–Au–Au junction shown in Fig. 4(f). For spin-up current, PDOS peaks −6.596 eV and −6.425 eV are on both sides of the forbidden region, and show stronger resistance to the itinerant electrons on the sides of the transmission valley. For spin-down current, the main transmission peak in Fig. 5(b) actually contains two transmission channels, which are represented by those two splitting spin-down PDOS peaks −6.154 eV and −5.943 eV. So the spin-down transmission peak is wider and higher, and spin-down electrons have a greater probability to transport through the Au–Au–Au junction.
After the rupture process, there are still both spin electrons distributed equally in the valence orbital of the center Au atom. Actually, the PDOS of the center Au atom at zero bias shows higher spin-up peaks and lower spin-down peaks as we specified spin +1/2, so the similar distributions at final bias 0.9 eV should be caused by itinerant electrons. When voltage is applied, spin-down electrons around Fermi energy have a small probability to tunnel from one anchor Au atom to the other. Since their energies are very close to the valence orbital of the center Au atom, their interaction may switch the spin state of the center Au atom. After this spin state switching, the spin-down electrons can transport easily through the spin resonance mechanism while the spin-up electrons transport by tunnelling and may switch the spin state again. The two spin states of the center Au atom will constantly change, so the PDOS distributions of spin-up and spin-down tend to be the same on average. If the current is spin polarized, according to the above discussion, the spin state of the center Au atom in the Au–Au–Au junction will switch to the corresponding direction, or rather, the Au–Au–Au junction can extract the spin information from the current. The energy of S valence orbitals is 0.8 eV higher than the one of the center Au atom, the tunnelling itinerant electrons are difficult to affect the spin state of the center Au atom, so the two anchor S atoms in the S–Au–S junction actually enhance the stability of the spin state stored in it.
4. ConclusionsWe have investigated electronic and spin transport properties of S–Au–S junction and Au–Au–Au junction by combining DFT and NEGF. Both junctions show the rupture process of the chemical bond between the anchor atom and the center Au atom at the distance of 3.5 Å. This bond breaking redistributes the spin state of the center Au atom and affects the characteristics of spin currents.
Current through these two junctions shows spin dependence. On the one hand, the valence electron of the center Au atom may resonate with itinerant electrons and enlarge the corresponding spin current. On the other hand, both chemical bonding and itinerant electrons can influence the spin state of the center Au atom. Such complicated interactions determine the final transport properties of our junctions.
Orbital energy shift made by different anchor atoms is a promising way to modulate the spin characteristics of different junctions. The high spin polarization and good spin stability of the S–Au–S junction can be used to store a certain spin state and extract its spin information to the current, while the spin direction switching property of the Au–Au–Au junction can extract current spin information into the center Au atom. The drifted Fermi energy and bias-dependent filtering property of the Au–Au–Au junction may be used as a control spin valve. With this kind of single atom junctions, we can read and write the spin state of a single Au atom by current. Thus the future logical circuit could not only be voltage dependent, but also distance dependent and spin dependent.