Recently, much attention has been paid to developing the stimuli-triggered nanocarriers that can effectively regulate drug release in response to a given stimulus (e.g., a change in pH, or in temperature, or in magnetic field).^[1–8] A DNA-based gatekeeper, as a potential candidate, provides new possibilities for the controlled drug delivery due to easy synthesis, high programmability, good biocompatibility, and efficient cellular uptake. In many applications, it is desirable to use solid surfaces as templates to guide DNA self-assembly or to maintain the stability of DNA-based nanostructures near surfaces.^[9–12]

It is well established that DNA molecules are negatively charged in a solution under physiological conditions (pH ≈ 7). Many efforts have been made to exploit DNA-gated nanocarriers for the controlled release upon exposure to a specific pH, enzyme action, and near-infrared light.^[9] A recent experiment on temperature-triggered DNA-gated nanocarrier performed by Yu et al.,^[13] demonstrates that, when carboxyl-modified single-stranded DNA (ssDNA) is anchored to the positively charged nanoparticle surface, the state of ssDNA is directly controlled by changing body temperature. According to the experimental results of Ref. [13], the critical release temperature of nanocarriers is with the DNA value of N > 10 (N is the number of bases). The sequences of 10, 20, 30, and 40 bases long ssDNA are 5’-COOH-(CH2)6-ACTCCTGGTA-3’, 5’-COOH-(CH2)6-ACTCCTGGTATGTAGCGCTA-3’, 5’-COOH-(CH2)6-ACTCCTGGTATGTAGCGCTAACTGTAATGG-3’, and 5’-COOH-(CH2)6–ACTCCTGGTATGTAGCGCTAACTGTAA TGGTCACGTCACT-3’, respectively.^[13] Nevertheless, the cargo molecules are released continuously at all the set temperatures if the length of the DNA valve is decreased to 10 bases. The experimental results imply that, for a 20–40 base long ssDNA chain, grafted ssDNA will stretch at high temperatures, and will collapse at low temperatures. For short ssDNA chains (N = 10), the temperature-dependent switching of ssDNA cannot happen. Understanding the behavior of DNA tethered to charged surface is needed to guide the above applications. Yamamoto et al.^[14] predicted the electric-field-dependent collapse of a polyelectrolyte brush grafted on an electrode using a mean field theory. Using molecular dynamics simulations, Robert et al.^[15] studied short ssDNA chains on model hydrophilic and hydrophobic self-assembled monolayers (SAMs), and elucidated the molecular interactions between the ssDNA, SAM, and water molecules. These ssDNA chains exhibit a favorable binding energy on both hydrophilic and hydrophobic SAMs. However, up to now, few theories have been devoted to a molecular-level understanding of temperature-dependent structure and switching of ssDNA tethered to a charged nanoparticle surface. Thus, it is necessary for us to include more molecular details to describe the structure and switching of ssDNA properly.

In this paper, motivated by the intriguing results of Ref. [13], we will present a molecular theory^[16–20] to explore how charged surfaces influence the structure and switching of ssDNA chains, and to explain the mechanism for temperature-dependent switching of ssDNA. The remaining part of this paper is organized as follows: in Section 2, we describe a molecular model; in Section 3, we present the results of investigating the temperature-dependent structure and switching of ssDNA tethered to a charged nanoparticle surface; we give conclusions and discussion in Section 4.

Amino-modified mesoporous silica nanoparticles (MSNs-NH₂) were selected.^[13] MSNs-NH₂ was positively charged. Carboxyl-modified ssDNA was anchored to the amino group on the surface of MSNs-NH₂.^[13] The system we consider is composed of ssDNA-grafted charged nanoparticles immersed in water. The nanoparticle with a radius R = 37 nm has its center at the origin of the r axis, and its surface is grafted by ssDNA. Carboxyl will not significantly affect the ssDNA grafting density. The grafting density is dependent on grafting temperatures, grafting reaction time, and molecular weight.^[21,22] The number of grafted chains per unit area, or grafting density, is σ = N_p/4πR². Our model ssDNA is a long chain with N segments (i.e., N bases), and each segment has a volume of v_p = 0.4 nm³.^[23] Water, proton, and hydroxyl ions are assumed to have the same volume of v_w = 0.03 nm³. The existence of nanoparticles induces an inhomogeneous distribution of all the molecular species, and the only inhomogeneous direction is assumed to be along the r axis. Considering the size, shape, and conformation of every molecular type explicitly, the Helmholtz free energy of the system is given by

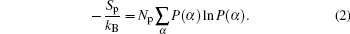
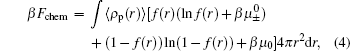
The third term on the right side of Eq. (1) is the translational entropy of small molecules including the protons, hydroxyl ions, and water. It is given by

The fourth term on the right side of Eq. (1) accounts for the electrostatic contribution (not including the interaction between the surface and charged polymer segments) to the free energy, and is determined by

The fifth term on the right side of Eq. (1) describes the interaction between the surface and charged polymer segments. This interaction is approximated by a Coulombic potential within a range of radius r, and the total attraction between the negatively charged polymer segments and the positively charged surface is thus given by

The last term of Eq. (1) is the system repulsive interactions and is written as

For the electrostatic potential, we obtain a generalized Poisson–Boltzmann equation

Equation (14) implies electrostatic contribution. Equation (6) does not include the interaction between the surface and charged polymer segments. The electrostatic attraction between the negatively charged polymer segments and the positively charged surface is only included in Eq. (8).

The expression for the fraction of the charged polymer segments at r is

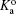
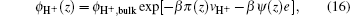
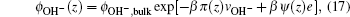
In a bulk solution, the acid–base equilibrium is determined by the equilibrium constant, .^[27] The equilibrium constant can be expressed as , where G is the free energy of the reaction.^[27] The volume fraction of protons, hydroxyl ions, and water are, respectively, given by

The bulk values of ions can be obtained from the ions concentration: ϕ_bulk,∓ = c_∓N_av_∓. The unknowns in the above equations are the position-dependent electrostatic and pressure fields. These quantities are determined by substituting Eqs. (12)–(18) into the packing constraints of Eqs. (10) and (11). A detailed numerical methodology is given in Appendix A of this paper.

In this section, we present some representative results for the structure and switching of ssDNA tethered to the charged nanoparticle surface.

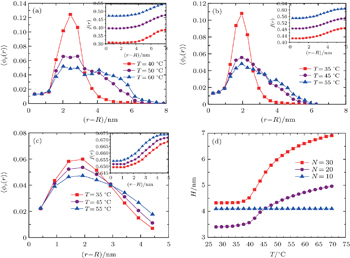
Figure 1 shows the relationship between average volume fraction of grafted ssDNA chains and temperature. From Fig. 1, it is easy to see that the grafted ssDNA chains stretch with increasing temperature and display a rather broad distribution at T = 52 °C. The distribution of ssDNA chain segments follows a parabolic profile at T = 42 °C, which means that the ssDNA chains are coiled. The height of ssDNA monolayer tethered to the charged nanoparticle surface H is defined as H = ∫ < ϕ_p(r) > r dr/∫ < ϕ_p (r) > dr, which measures the amount of stretching of grafted ssDNA chains. In the same way, we show a strong dependence of the ssDNA monolayer height on temperature in Fig. 2, from which the grafted ssDNA stretches with increasing temperature, and the switching is presented at T = 46 °C. In the previous experiment,^[13] the ssDNA chains were indeed reported to stretch with further increase in temperature. In order to understand the origin of this behavior, we calculate the electrostatic potential, which is also a temperature-dependent quantity. Figure 3 shows the distribution of electrostatic potential inside the ssDNA monolayer at different temperatures. It should be stressed that all the charged species in solutions contribute to the electrostatic potential. The electrostatic potential of the complex displays negative values at all the temperatures. The negative electrostatic potential inside the ssDNA monolayer implies an electrostatic repulsion between the negatively charged ssDNA segments. The insertion of charged monomers into a varying electrostatic potential is thus energetically unfavorable. With the decrease in temperature, the degree of dissociation increases considerably, the acid–base equilibrium of the ssDNA chains shifts towards the charged state, and the ssDNA becomes more negatively charged. Since the electrostatic potential displays negative values and decreases with increasing temperature, elastic energy of ssDNA and the electrostatic repulsions will overcome electrostatic attractions between the negatively charged polymer segments, causing the polymer chain to stretch.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Average volume fractions of grafted ssDNA chains as a function of the distance from the nanoparticle surface at different temperatures. The number of segments of grafted ssDNA chains is N = 40. The grafting density is σ = 0.5 nm−2.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Height of grafted ssDNA chains as a function of temperature. The number of segments of grafted ssDNA chains is N = 40. The grafting density is σ = 0.5 nm−2.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Electrostatic potential as a function of the distance from the nanoparticle surface at different temperatures. The number of segments of the ssDNA chains is N = 40. The grafting density is σ = 0.5 nm−2.

In order to understand the origin of this behavior, we analyze the switching of ssDNA tethered to the charged nanoparticle surface in terms of varying chain length and behavior of charged ssDNA chains, and produce the diagrams of local average volume fractions as a function of distance from the nanoparticle surface, as shown in Figs. 4(a)–4(c).

Fig. 4.

Figure Option ViewDownloadNew Window

Fig. 4. The average volume fractions of the grafted ssDNA chains as a function of distance from the nanoparticle surface at different temperatures for (a) N = 30, (b) N = 20, and (c) N = 10. The insets show the degree of dissociation as a function of distance from the nanoparticle surface. (d) The height of grafted ssDNA layer as a function of temperature for different N. The grafting density is σ = 0.5 nm−2.

Figure 4 illustrates an average volume fraction of the charged ssDNA chains at different temperatures for different chain lengths. The long ssDNA chains (N = 30 and N = 20) show similar behavior: at a high temperature they are stretched more than at a low temperature. However, unlike the long ssDNA chains, the short ssDNA chains (N = 10) qualitatively show different switching behaviors, as recognized by Yu et al.^[13] The short ssDNA chains show a weak dependence of their switching on temperature, as shown in Fig. (4). The insets in Fig. 4 schematically show the degree of dissociation as a function of distance from the charged nanoparticle surface. For the long ssDNA chains, there are big differences between the degree of dissociation at high temperatures and that at low temperatures. For the short ssDNA chains, the differences between the dissociation degree at high temperatures and that at low temperatures are smaller. Figure 4(d) shows that the switching of the short ssDNA chains cannot occur. This is because the electrostatic attractions between negatively charged polymer segments and positively charged surface are insufficient to overcome the elastic free energy of ssDNA and electrostatic repulsion energy.

It is worthwhile to note that the screened Coulombic interactions give rise to a negative pressure, and counterions result in an entropic pressure, which can induce the collapse of the polyelectrolyte.^[14] The counterion-mediated attractive interactions along a chain can also lead to a collapse of a single chain, endowing the chain with a very compact structure and an inhomogeneous distribution. To explore the screened Coulombic interactions and attractive interactions along chains, we investigate distributions of H⁺ and OH⁻, and produce the diagrams of local fractions of local concentration of H⁺ and OH⁻ as a function of distance from the charged nanoparticle surface at different temperatures, as shown in Figs. 5(a) and 5(b). One can see that the local concentrations of both H⁺ and OH⁻ near charged nanoparticle surface are significantly lower than those of bulk water. Therefore, we expect that the attractive interactions along chains cannot be attributed to screened Coulombic interactions and H⁺ mediated electrostatic attractions among ssDNA chains. This is because the complex of electrostatic attractions, elastic energy of ssDNA and electrostatic repulsion play a dominant role.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Local concentration of (a) H+ and (b) OH− as a function of the distance from the nanoparticle surface.

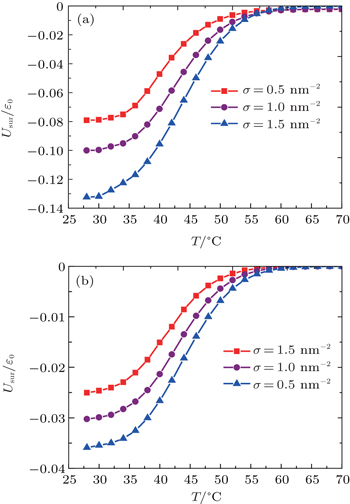
So far, we have discussed the temperature effect on the self-assembly of ssDNA chains. To further verify the structure and switching of ssDNA tethered to the charged nanoparticle surface, it is instructive to reflect on Eq. (8), the expression of the interaction between the surface and charged polymer segments, U_surf. According to our model, U_surf represents the attraction between the negatively charged ssDNA segments and the positively charged nanoparticle surface.

As illustrated in Fig. 6, the quantity of U_surf/ε₀ is a function of temperature at different grafting densities. From Fig. 6, for the long ssDNA chains (N = 40), U_surf/ε₀ increases with increasing temperature. This implies that once the temperature is above the critical temperature, the electrostatic attractive interaction between ssDNA and charged nanoparticle surface becomes weak dramatically, which leads to a stretch of ssDNA. Thus, the switching of ssDNA can happen, and the critical temperature exists, due to the electrostatic interaction between DNA and the charged nanoparticle surface. For the short ssDNA chains (N = 10), U_surf/ε₀ shows a slight change when the temperature increases. This indicated that the critical switching temperature of the short ssDNA chains does not exist. When the length of ssDNA chains is decreased to 10 bases, there is no obvious difference in the structure of ssDNA chains. The reason for this is that the electrostatic attraction is insufficient to overcome the elastic free energy of ssDNA and electrostatic repulsion energy, and the short ssDNA chains are more flexible than the long ssDNA chains.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Electrostatic attraction potential between negatively charged polymer segments and positively charged surface as a function of the distance from the nanoparticle surface for (a) N = 40 and (b) N = 10. Parameters are the same as those in Figs. 1 and 3.

For practical applications of DNA-gated nanocarriers,^[13] grafting density must be controllable. Choosing different temperatures, we intend to see the impact of H on grafting density. Figure 7 illustrates that the height H varies with grafting density for both the long and short ssDNA chains. For the long (N = 40) ssDNA chains, as the temperature is fixed, the H increases with grafting density. For the short (N = 10) ssDNA chains, H exhibits a maximum at about σ = 0.3 nm⁻² and σ = 0.6 nm⁻² for T = 45 °C and T = 35 °C, respectively. This effect could be caused by the increase in the fraction of charged ssDNA segments, which leads to an increase in electrostatic attractions between the negatively charged ssDNA segments and the positively charged nanoparticle surface.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. The height of the grafted ssDNA layer as a function of the grafting density for (a) N = 40 and (b) N = 10.

In order to quantify the charging behavior of the ssDNA chains in response to changes in grafting density, we define the average fraction^[27,28] of the charged polyelectrolyte monomers by

Figure 8 illustrates the average fraction of the charged ssDNA monomers as a function of grafting density. More importantly, we find that the transition of charged behavior occurs as grafting density increases, because there are more freedom degrees when the ssDNA chains respond to varying grafting density, and only the fraction of charged ssDNA monomers can be changed as a consequence of variation in grafting density.

Fig. 8.

	Figure Option ViewDownloadNew Window
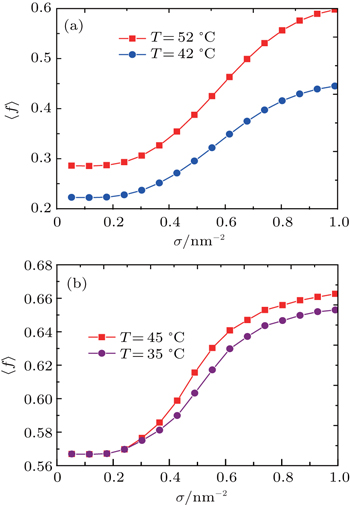	Fig. 8. The average fraction of charged polyelectrolyte monomers as a function of grafting density for (a) N = 40 and (b) N = 10.

Figure 8 shows that most ssDNA molecules in long chains (N = 40) are uncharged in the case of a low grafting density. Increasing the grafting density would result in a large electrostatic repulsion between ssDNA chains and ssDNA chains, which is favorable for ssDNA chain monomers to remain charged at the cost of free energy of the acid–base reaction. In the case of a high grafting density, increasing the grafting density would result in very little free volume. Because of the limited available volume, the charged chains must extend from the surface due to repulsion with simultaneous loss of conformational entropy and increasing entropy of counterions.

To gain greater entropy and to reduce the energy cost from ssDNA intermolecular repulsions, it will be favorable for many monomers to remain charged. However, most ssDNA molecules in short ssDNA chains (N = 10) are charged. Thus, ⟨f⟩ represents slightly nonmonotonic change in response to increasing grafting density, as shown in Fig. 8(b). Compared with the long ssDNA chains, the short ssDNA chains have smaller conformational entropy. In this case, ssDNA can only slightly modify its charge as a response to an external stimulus. It has to be pointed out that the values of ⟨f⟩ of weak polyelectrolyte depend on many parameters. In addition to pH, the salt concentration and thickness of monolayers also affect the values of ⟨f⟩.^[24] However, studying the relation between ⟨f⟩ and such parameters is beyond the scope of this work. Based on our theoretical model, we predict that the switching of ssDNA cannot happen if the grafting densities are too high, due to an increase in monomer–monomer repulsive interaction. This provides a good guide for precisely controlling the self-assembly of ssDNA tethered to a charged nanoparticle surface.

We have employed a molecular theory to study the temperature-dependent structure and switching of ssDNA tethered to a charged nanoparticle surface. For the longer (N > 10) ssDNA chains, they adopt a compact conformation on the bottom of a layer at low temperatures, while the inverse transformation will take place at high temperatures. The electrostatic attractive interaction between the ssDNA and charged nanoparticle surface weakens as temperature increases. When the electrostatic attractive interaction cannot overcome the elastic energy of ssDNA and electrostatic repulsion energy, ssDNA chains will stretch. For the short (N = 10) ssDNA chains, the switching of ssDNA cannot happen, and the critical temperature does not exist. This is because, in all ranges of temperature, the electrostatic attraction interaction between the negatively charged polymer segments and the positively charged surface is insufficient to overcome the elastic energy of ssDNA and electrostatic repulsion energy along ssDNA chains. This accords well with the experimental observations^[13] of ssDNA at different temperatures, and reveals the unique temperature-dependent structure and switching behavior of the ssDNA tethered to a charged nanoparticle surface.^[13] According to our theoretical model, we can predict that if the grafting densities are too high, the switching of ssDNA cannot happen.

Our theoretical approach has general characteristics, which will be applied to other molecule systems, such as single-stranded PNA and single-stranded RNA.^[31–36] These molecule systems have a great potential for applications in biomaterials. It is worth mentioning that experiments in previous studies were carried out under nonequilibrium conditions. However, we believe that main temperature-dependent switching of ssDNA tethered to a charged nanoparticle surface is captured by our equilibrium approach. The slow non-equilibrium kinetics, as observed in the experiments of Ref. [13], can lead to lateral phase separation,^[37] making the ssDNA tethered to charged nanoparticle surface density nonhomogenous. It is necessary to build a theoretical model by taking into account a three-dimensional nonequilibrium system. Advances in theory,^[38–43] combined with experimental observations, will enable us to modify the designs of biopolymer surfaces for a large variety of applications.