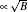† Corresponding author. E-mail:
In this paper, a new model is proposed for manipulating the Kerr nonlinearity of right-hand circular probe light in a monolayer of graphene nanostructure. By using the density matrix equations and quantum optical approach, the third-order susceptibility of probe light is explored numerically. It is realized that the enhanced Kerr nonlinearity with zero linear absorption can be provided by selecting the appropriate quantities of controllable parameters, such as Rabi frequency and elliptical parameter of elliptical polarized coupling field. Our results may be useful applications in future all-optical system devices in nanostructures.
Electromagnetically induced transparency (EIT),[1] in atomic systems and semiconductor quantum wells and quantum dot structures has led to many unforeseen phenomena such as lasing without inversion,[2] four-wave mixing,[3,4] and so on.[5–15] EIT exploits destructive quantum interference to make an otherwise opaque medium almost transparent. This feature of EIT medium (transparent to the applied fields) makes it suitable for application in nonlinear optical science. In nonlinear optics, it is favorable to have a strong nonlinear medium in low light intensities. Therefore, Kerr nonlinearity of such medium plays essential roles for studying some other phenomena which require strong nonlinear medium such as quantum nondemolition measurements,[16] quantum bit regeneration,[17] quantum state teleportation,[18] and the generation of the optical solitons.[19] The Kerr nonlinearity of the medium corresponds to the real part of third-order susceptibility of weak probe light which propagates through it. The features of Kerr nonlinearity of weak probe light in multi-level atomic systems have been reported by many research groups.[20–29] It has been shown that the Kerr nonlinearity can be manipulated by many different mechanisms. For instance, Niu et al. proposed a model for giant Kerr-nonlinearity-based spontaneously generated coherence (SGC) in a usual three-level atomic system.[26] In another study done by Niu et al., the role of the double dark resonances on Kerr nonlinearity has been discussed.[27] Asadpour et al.[28] proposed a model for studying the enhanced Kerr nonlinearity via quantum interference from spontaneous emission. The properties of Kerr nonlinearity in a semiconductor quantum well and quantum dot-based different mechanisms have also been investigated.[30–35] For instance, phase control of Kerr nonlinearity in a quantum well nanostructure has been suggested by Asadpour et al.[30] The role of biexciton coherence on Kerr nonlinearity of probe light propagated in a multiple quantum well nanostructure has also been reported.[33] Moreover, it has been found that exciton spin relaxation can lead to manipulating of Kerr nonlinearity in a multiple quantum well nanostructure.[34] The giant Kerr nonlinearity in a crystal of molecular magnet has also been discussed.[35]
On the other hand, the optical and electronic features of graphene nanostructure due to its important usages in condense matter and optical physics have been investigated recently.[36–39] The properties of electrons near the Dirac points make it possible for interacting by electromagnetic fields.[40–42] The nonlinear optical features of graphene nanostructure in the presence of strong magnetic field has been discussed very recently in four-wave mixing,[43,44] generation of polarized-entangle photon, nonlinear frequency conversion of THz surface plasmons based on the nonlinear optical interaction,[45,47] optical bistability,[48,49] and slow and fast light propagating.[50] To the best of our knowledge, the enhanced Kerr nonlinearity of graphene with zero linear and nonlinear absorption has not been reported theoretically or experimentally. In this paper, we suggest a model based on the quantized four-level graphene nanostructure for enhancing the Kerr nonlinearity by using a probe and an elliptical polarized control field. We show that by selecting appropriate values for Rabi frequency and elliptical parameter of control field, the Kerr nonlinearity can be enhanced at certain values of probe field detuning.
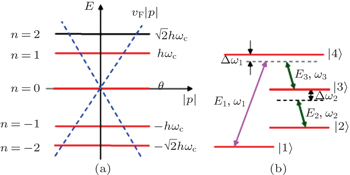
A single layer of graphene system in the presence of strong magnetic field is presented in a four-level scheme (Fig. 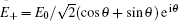
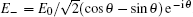


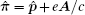

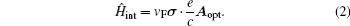
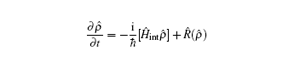

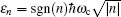

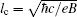
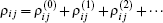

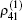
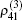
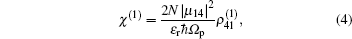
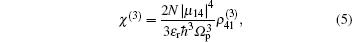
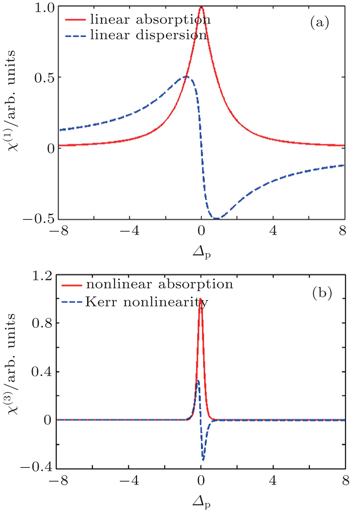
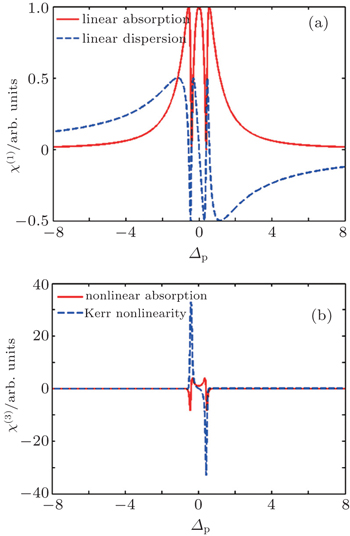
In the following section, we will analyze the third-order susceptibility through numerical simulations in detail. According to the numerical estimate based on Refs. [43]–[50], we can take a reasonable value for the decay rate and all parameters are scaled by decay rate γ. This value depends on the sample quality and the substrate used in experiments.[51,52] The electron concentration is N ≃ 5 × 1012 cm−2 and the substrate dielectric constant is εr ≃ 4.5.[53–55] The linear and nonlinear features of the susceptibility for parameter θ = 0 are explored in Fig.
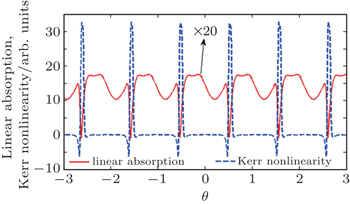 | Fig. 4. Linear absorption (solid line) and Kerr nonlinearity (dashed line) versus elliptical parameter θ. The selected parameters are the same as Fig. |
 | Fig. 5. Linear absorption (solid line) and Kerr nonlinearity (dashed line) versus different quantities of Rabi frequency Ωc for (a) θ = 0 and (b) θ = π/6. The other parameters are the same as Fig. |
Similar to the laser-driven atomic medium or ensemble consisting of many single atoms,[57] here we only consider a graphene monolayer in the graphene ensemble interacting with optical fields for the sake of simplification of the calculation. It should be emphasized that the optical conductivity of a graphene layer is proportional to its effective thickness or surface density of atoms.[58,59] This is in spite of the fact that the effective thickness of a graphene layer is around one angstrom and the vacuum wavelength of the optical waves under consideration is around one micron. However, through our calculation and analysis, it is possible to observe such spatial solitons by use of the graphene ensemble. In view of rapid advances in graphene material, we believe that the formation of matched infrared soliton pairs will be accessible in experiments in the near future.
In summary, the linear and nonlinear susceptibilities of the monolayer graphene system driven by a probe and elliptical polarized coupling fields are explored by using the density matrix formalism. Our numerical results show that by tuning the elliptical parameter of elliptical polarized coupling field, the Rabi frequencies of coupling fields can be modified. Therefore, the enhanced Kerr nonlinearity with vanishing of linear absorption can be provided in two detunings of probe field.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 |