† Corresponding author. E-mail:
Project supported by the Nanyang Normal University Science Foundation of China (Grant No. ZX2013017) and the National Natural Science Foundation of China (Grant Nos. 11174066, 61306007, and U1304114).
We make a detailed study on the angular differential cross sections of positron–hydrogen collisions by using the momentum-space coupled-channels optical (CCO) method for incident energies below the H ionization threshold. The target continuum and the positronium (Ps) formation channels are included in the coupled-channels calculations via a complex equivalent-local optical potential. The critical points, which show minima in the differential cross sections, as a function of the scattering angle and the incident energy are investigated. The resonances in the angular differential cross sections are reported for the first time in this energy range. The effects of the target continuum and the Ps formation channels on the different cross sections are discussed.
The study of positron collisions with atoms has served as a fundamental testing ground for our understanding of particle and antiparticle interacting with atoms.[1] Due to its simplicity and fundamental importance, the positron collision with a hydrogen atom is very useful in the development of theoretical techniques for more complicated systems. One of the active areas in positron–atoms interactions, which has attracted considerable theoretical interest, is the resonances involving the positron.[2,3]
The resonances in positron–hydrogen scattering play an important role in the production of anti-hydrogen atoms through the rearrangement scattering of positronium by anti-proton.[4–6] Even though there are not yet any reports of experimental observations, several theoretical methods have been used to demonstrate the existence of resonances in this system, including the method of complex-coordinate rotation,[7–9] the close-coupling method,[10–12] the hyperspherical close-coupling method,[13,14] the Harris–Nesbet variational method,[15,16] the stabilization method,[17–19] and the stochastic variational method.[20] However, most of these calculations are either limited to a specific one partial wave or constrained to resonance structures in total cross sections. In this work, we present resonances in angular differential cross sections and investigate the variation of the resonances along with the scattering angle. Theoretical study of differential cross sections is of great importance in collisional phenomena not only because the measurements are expressed by means of this quantity, but also because this quantity characterizes the details of the collisional dynamics. The nature of the differential cross section is generally characterized by its behavior around the critical points which are defined to the scattering angles at which the differential cross section has a deep minimum for specific incident energy. The critical points were first investigated by Buhring[21] in electron–atom systems. The author analyzed the origin of these critical points and demonstrated the same causations for positron and electron scatterings. Several methods have been used to investigate the existence of the critical points for positron–atom collisions. Wadhera et al.[22] predicted the existence of critical points for positron–rare-gas-atom collisions by using empirical relationships satisfied by the phase shift. Then Mandal et al.[23] and Ghoshal et al.[24] predicted the existence and the behavior of critical angles in elastic positron–hydrogen collisions using the state-of-the-art Schwinger variational method.
Comparing with a large number of previous works on the resonances in the positron–hydrogen system, only a few involve research on the resonance properties in angular differential cross sections. The studies of the angular dependence of the scattering cross section offer a special tool to investigate the resonances in more detail. In this work, our main object is to make a detailed study on the resonance features and the critical points of angular differential cross sections in positron–hydrogen scattering employing the momentum-space coupled-channels optical (CCO) method.[25] The CCO method for electron–atom collision given by McCarthy and Stelbovics[26] has been applied to calculate the energy-dependent phenomena in electron–hydrogen scattering[27] and negative-ion resonances in electron–sodium[28] and electron–oxygen[29] systems. Good agreements with experiments and other calculations have been achieved. Recently, the CCO method for positron–atom scattering given by Zhou et al.[25] has been applied to study the energy-dependent phenomena in positron–atom systems.[30–34] In our previous work,[32,33] the energy-dependent phenomena and the resonance structures in the positron–hydrogen system have been studied in the framework of the CCO model. An equivalent local polarization potential has been used to describe the target ionization continuum and the positronium (Ps) formation rearrangement channels and therefore this method can ideally take the contributions of all reaction channels into account. The method has been applied to calculate various scattering cross sections (positronium formation, ionization, and total scattering cross sections) for the positron–hydrogen system and satisfactory results have been obtained comparing with experimental data and other theoretical calculations.[32,33]
A detailed theoretical description of the CCO method has been given in the paper of Zhou et al.[25] and also in our previous work.[32–34] Here we outline the essential features of this method. The total scattering cross section is calculated by solving the momentum-space coupled-channels equations[26]



The optical potential describing the positronium formation is

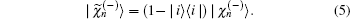
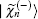


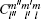

For computation, we make the partial-wave expansion of the T and V(Q) matrix elements by defining the partial-wave matrix elements


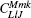
The differential cross section for scattering from channel j to channel i at angle θ is
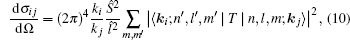

Once the scattering cross sections are obtained at various incident energies, the position and width of the resonance for a particular value of J can be obtained by fitting the Breit–Wigner formula with a linear background

In the present calculations, the P space consists of fifteen states, including 1s, 2s, 3s, 4s, 5s, 6s; 2p, 3p, 4p, 5p, 6p; 3d, 4d, 5d, 6d. The optical potentials describing the target ionization continuum are included in the channel couplings of 1s–1s, 1s–2s, 1s–2p. The optical potentials describing the positronium formation in the corresponding Ps(n = 1) and n = 2 states are included in the above 1s–1s channel coupling. The optical potentials in other channel couplings have a small effect on the cross sections and therefore can be ignored. With the absence of any optical potentials, the normal close-coupling (CC) method is revisited.
We have done the calculations from 6.5 eV to 13.5 eV at an interval of 0.5 eV. In order to make an in-depth study of the angular differential cross section, we make use of surface plots. The results of the elastic differential cross sections are presented in Fig.
 | Fig. 1. The elastic differential cross section as a function of positron incident energy (6.5–13.5 eV) and scattering angle (0–180°). |
| Table 1. The critical angles and the corresponding differential cross sections in elastic positron–hydrogen collisions at incident positron energies from 6.5 eV to 13.5 eV. . |
 | Fig. 2. Comparison of the present critical angles in elastic differential cross sections with the prediction of Ghoshal and Mandal.[24] |
To have a transparent idea about the critical angles, we plot in Fig.
In our preceding paper,[32] we have reported the energy-dependent phenomena above the H(n = 2) threshold for positron collisions with hydrogen in partial wave cross sections. The calculations are based on the CCO method and agree reasonably well with other available theoretical calculations such as those of Ho and Yan.[9] In this work, we perform the calculations at an interval of 0.001 eV in the vicinity of the resonance energy region and investigate the resonance structure in the angular differential cross sections. The results for selected angles of 50°, 80°, 135°, and 180° are shown in Fig.
 | Fig. 4. The differential cross sections at (a) 50°, (b) 80°, (c) 135°, and (d) 180°. The positions of resonances are indicated by the arrows. |
In order to investigate the effects of the target continuum and the positronium formation channels on the resonances, we have carried out the CC15 calculations. The results are shown in Table
| Table 2. Comparison of resonance energies by CC15 and CCO models in e+–H scattering. The ER and ΓR are in units of eV. . |
We report some of the dramatic behaviors in the differential cross sections of e+–H scattering. By using the momentum-space coupled-channel optical method, all reaction channels for positron–atom scatterings are included in the calculations with appropriate approximations. The critical points found in the angular differential cross sections are in good agreement with those reported by Ghoshal and Mandal.[24] The resonance structures are shown to have different structures at different scattering angles and further works are needed to shed more light on such phenomenon. The effects of the target continuum and the positronium formation channels on both the critical angles and the resonance parameters are investigated. It is shown that the contributions are very important in producing the correct shape of the differential cross sections and physically complete resonance width. It is hoped that our present work on resonances would provide useful information for future research.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 |



