† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2012CB922103) and the National Natural Science Foundation of China (Grant Nos. 11274104 and 11404108).
The temporal evolution of the degree of entanglement between two atoms in a system of the binomial optical field interacting with two arbitrary entangled atoms is investigated. The influence of the strength of the dipole–dipole interaction between two atoms, probabilities of the Bernoulli trial, and particle number of the binomial optical field on the temporal evolution of the atomic entanglement are discussed. The result shows that the two atoms are always in the entanglement state. Moreover, if and only if the two atoms are initially in the maximally entangled state, the entanglement evolution is not affected by the parameters, and the degree of entanglement is always kept as 1.
In quantum physics, the entanglement states of two or more particles have not only played a vital role in the discussion of nonlocal quantum correlations,[1] but also formed the basis of quantum communication and information processing, such as quantum computation,[2] quantum cryptography,[3] quantum teleportation,[4] and quantum dense coding.[5] For a bipartite pure state it is straightforward, that there has been a lot of work on bipartite entanglement. For example, with the von Neumann entropy,[6–15] distance between density operators,[16,17] fidelity,[18,19] negative eigenvalue,[20–23] and concurrence.[24] Recently, more and more researchers are paying attention to the non-orthogonality entangled coherent state.[25–28] Researching the entanglement properties of two two-level atoms interacting with the two-mode non-orthogonality entangled coherent state which has symmetry in phase space may be the vital practical significance and application.[29]
In this paper, based on the negative eigenvalue, which can be used to measure the quantum entanglement between two particles, we investigated the system which consists of two identical two-level atoms resonantly interacting with the binomial optical field. Consider that two atoms A, B are initially in an arbitrary Bell state and coupled to a cavity, simultaneously. The influence of the strength of the dipole–dipole interaction between two atoms, probabilities of the Bernoulli trial and the particle number of the binomial optical field are discussed by using full quantum theory and a numerical processing method.
Our paper is organized as follows. In Section 2, the theory model and state-vector equations solution are given. In Section 3, the negative eigenvalue of two two-level atoms in an entangled state interacting with the binomial optical field is investigated. Finally, the discussion and a brief summary are shown in Section 4.
We consider the case that two identical two-level atoms A and B are simultaneously injected into a binomial optical cavity. Assuming that the distance between atoms is smaller than the wavelength of the cavity field, made by exchanging between atoms produced by the virtual photons, the dipole–dipole interaction should not be neglected, and there are the same couplings of the two atoms as interacting with a binomial optical field. Under these conditions, the effective Hamiltonian in the rotating wave approximation can be written as (ħ = 1)

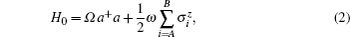
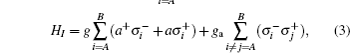
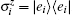
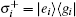
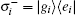
We consider that at t = 0, two two-level atoms are in the entangled state

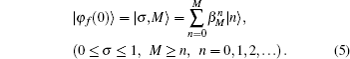

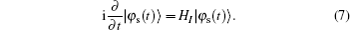
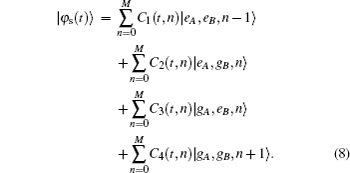
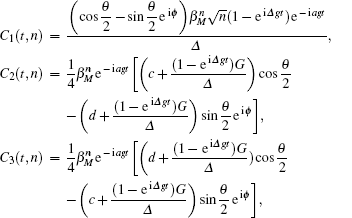
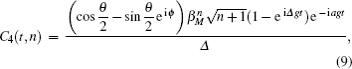
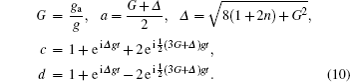
For two subsystems in the mixed state, we may use the negative eigenvalues of partial transposition of density matrix as a measurement of the degree of entanglement between the two subsystems. Consider a density matrix ρ(t) and its partial transposition ρT(t) for a system of two spin-1/2. The measure of entanglement EAB(t) is then defined by[30]
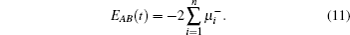


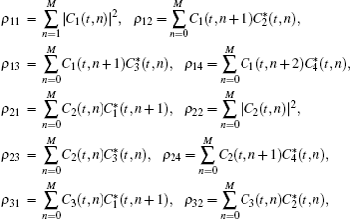

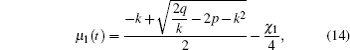
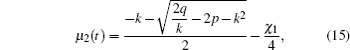
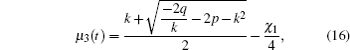
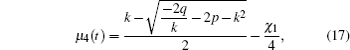
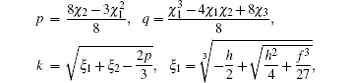
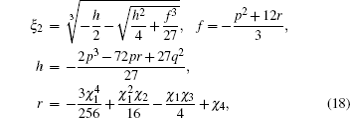

According to the above theory, we can conveniently obtain quantum entanglement between two atoms, corresponding to three different atomic initial states and parameters respectively, shown in Figs.
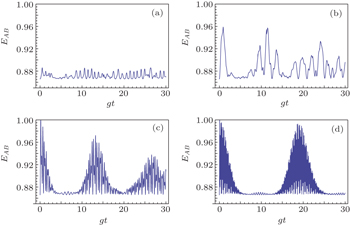 | Fig. 1. Time evolution of EAB versus θ = π/3, or θ = 2π/3 for different G. The parameters are ϕ = 0, M = 5, and σ = 0.5. From panel (a) to panel (d): G = 0; G = 1; G = 5; G = 10. |
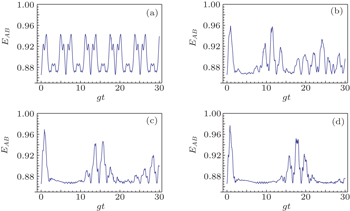 | Fig. 2. Time evolution of EAB versus θ = π/3, or θ = 2π/3 for different M. The parameters are ϕ = 0, G = 1, and σ = 0.5. From panel (a) to panel (d): M = 1; M = 5; M = 10; M = 15. |
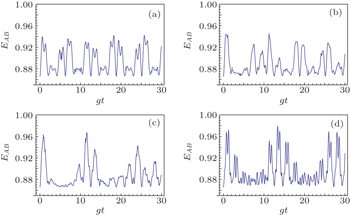 | Fig. 3. Time evolution of EAB versus θ = π/3, or θ = 2π/3 for different σ. The parameters are ϕ = 0, M = 5, and G = 1. From panel (a) to panel (d): σ = 0.1; σ = 0.3; σ = 0.6; σ = 0.9. |
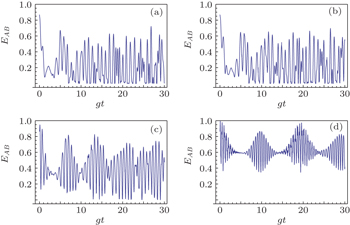 | Fig. 4. Time evolution of EAB versus θ = π/3, or θ = 2π/3 for different G. The parameters are ϕ = π, M = 5, and σ = 0.5. From panel (a) to panel (d): G = 0; G = 1; G = 5; G = 10. |
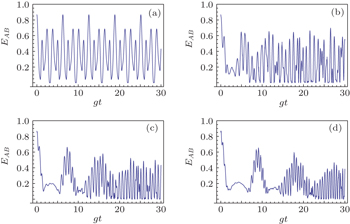 | Fig. 5. Time evolution of EAB versus θ = π/3, or θ = 2π/3 for different M. The parameters are ϕ = π, G = 1, and σ = 0.5. From panel (a) to panel (d): M = 1; M = 5; M = 10; M = 15. |
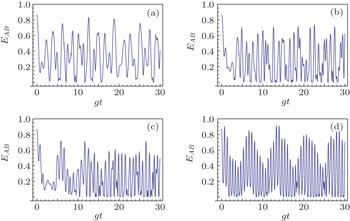 | Fig. 6. Time evolution of EAB versus θ = π/3, or θ = 2π/3 for different σ. The parameters are ϕ = π, M = 5, and G = 1. From panel (a) to panel (d): σ = 0.1; σ = 0.3; σ = 0.6; σ = 0.9. |
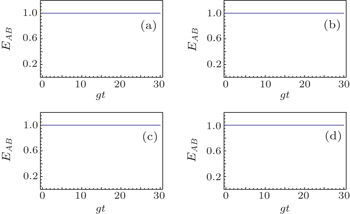 | Fig. 7. Time evolution of EAB versus θ = π/2 for different σ. The parameters are ϕ = 0 or ϕ = π, M = 5, and G = 1. From panel (a) to panel (d): σ = 0.1; σ = 0.3; σ = 0.6; σ = 0.9. |
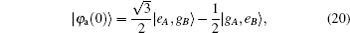
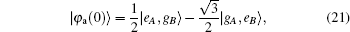
In Fig.
In Fig.
In Fig.
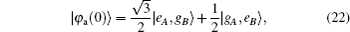

In Fig.
Homologous, the chosen parameters G and σ in Fig.
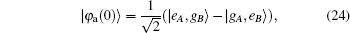
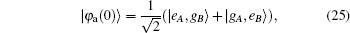
In Case 3, with certain parameters, we obtained the temporal evolution of EAB in Fig.
In conclusion, the temporal evolution of the degree of entanglement between two atoms in a system of two entangled atoms interacting with the binomial optical field has been studied. The influence of the strength of the dipole–dipole interaction between two atoms, probabilities of the Bernoulli trial, and particle number of the binomial optical field on the time evolution of the atomic entanglement are discussed. The result shows that the two atoms are always in the entanglement state. Moreover, an interesting phenomenon is that when and only when the two atoms are initially in the maximally entangled state, the entanglement evolution between two atoms is not affected by the parameters, and the degree of entanglement is always kept as 1. This result will be helpful for the understanding of entanglement by further investigation of the entangled atoms interacting with all kinds of fields.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 |


