† Corresponding author. E-mail:
Project supported by the South African Research Chair Initiative of the Department of Science and Technology and National Research Foundation.
We investigate the effect of collective-rotation noise on the security of the six-state quantum key distribution. We study the case where the eavesdropper, Eve, performs an intercept-resend attack on the quantum communication between Alice, the sender, and Bob, the receiver. We first derive the collective-rotation noise model for the six-state protocol and then parameterize the mutual information between Alice and Eve. We then derive quantum bit error rate for three intercept-resend attack scenarios. We observe that the six-state protocol is robust against intercept-resend attacks on collective rotation noise channels when the rotation angle is kept within certain bounds.
Quantum key distribution (QKD) provides the only physically secure and proven method to exchange secret cryptographic keys between two parties, Alice and Bob,[1,2] through public communication channels. QKD guarantees that an eavesdropper, Eve, with full access to the communication channels and unbounded computational power is unable to extract useful information on secret keys exchanged.[2] Unlike the conjectured security of classical key distribution,[3,4] which rely on the implied difficulty of solving discrete logarithm and integer factorisation problems, the security of QKD is based on the fundamental laws of physics, for example, the no-cloning theorem[5] and the Heisenberg uncertainty principle.[6–8] This means that in principle QKD guarantees unconditional security in communication between legitimate users if perfectly implemented.[2]
Since Bennett and Brassard’s pioneering work of the BB84 protocol,[1] several QKD protocols have been proposed,[9–12] reviewed and implemented.[13–28] Furthermore, these developments have led to commercialization of QKD.[29,30]
In security studies, the noise in the quantum channel requires scrutiny because an eavesdropper trying to avoid detection may disguise themselves as noise.[31] Precisely, the noise pattern of the channel can be controlled by an eavesdropper. A number of studies on the effect of noise on QKD have been published. For example, the security of the Bennett 1992 QKD against individual attack over a realistic channel,[32] and over a lossy and noisy channel.[33] Likewise, the effect of quantum noise on the achievable finite-key rates of the BB84 and the six-state protocols has also been presented in Ref. [34].
Photons are the best carriers of quantum information in current QKD set-ups and the majority of the commercial systems use optical fibre as the communication channel. However, optical fibres suffer from slow fluctuations in the birefringence, which can be modeled as collective noise.[31] Therefore, noise is highly unavoidable in the communication process. There are two main types of collective noise namely, collective-dephasing noise and collective-rotation noise. In general, noise poses a threat especially for QKD schemes that implement a polarization degree of freedom for encoding information. This is because the noise usually changes the fidelity of quantum states that carry quantum information and also allows an eavesdropper to disguise her disturbance as noise in the communication channel, thus reducing her detection probability. Only when the noise, i.e., error rates are acceptable can the legitimate parties use the quantum signals to generate a secret key. Otherwise, if the noise is too large, this results in a high error rate, therefore no secret key can be extracted. Collective noise is the noise that has the same effect on adjacent quantum systems. Several studies have been published on the effects of collective-dephasing and collective-rotation noises on quantum communication, see Refs. [35]–[39]. Given a qubit, collective-dephasing noise introduces phase in one of the two basis states. This phase, however, does not affect the statistics of measurement in the preparation basis. Collective-rotation noise, on the other hand, alters the statistics by introducing a probability of inverting one basis state into the other.
The aim of this study is to demonstrate the security bounds for the six-state QKD protocol,[11] which was designed to be more resistant to noise, when collective-rotation noise is present in the transmission channel. This article is arranged as follows. In Section 2, we give a brief description of the operation of the six-state QKD protocol. In Sections 3 and 4, we describe the scheme for collective noise rotation and analyze the effect of the noise on the operation of the protocol. We conclude the article in Section 5.
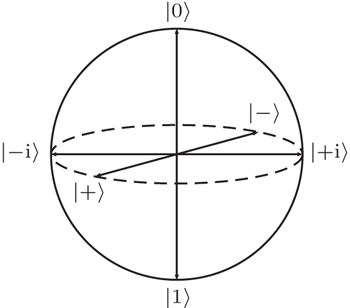
The six-state protocol[40] is a more generalized version of the BB84 protocol,[1] in which information is randomly encoded in three bases: {|0〉, |1〉}, {|+〉, |−〉}, and {| + i〉,| − i〉} bases, where 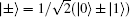

| Table 1. Representation of the six states in the three bases. . |
In the six-state protocol, Alice creates a random bit string and randomly selects one of the three bases, with equal probability p = 1/3, to encode each bit in the string. She sends the resultant qubit stream to Bob using a quantum channel. Bob randomly chooses, with probability 1/3, the basis in which he measures the state of each qubit in the stream. Bob’s observables are given by the following Pauli operators: σz, σx, and σy for the {|0〉, |1〉}, {|+〉, |−〉}, and {| + i〉,| − i〉} bases, respectively. Following Bob’s measurements, Alice communicates the random basis selection through an authenticated classical channel. They both discard measurements where Bob used a different basis, in a process called sifting, and apply classical post-processing techniques on the remaining events to distil a secret key.
The six-state QKD protocol has been studied under various scenarios since its proposal. Based on the optimal mutual information between sender and eavesdropper, it has been shown that the six-state scheme is safer against eavesdropping on single qubits than the one based on two conjugate bases.[40] A study of optimal eavesdropping strategies for the six-state QKD protocol has been made and the results show that this scheme is more secure against symmetric attacks than protocols using two-dimensional states.[45] Furthermore, incoherent and coherent eavesdropping strategies on the six-state protocol have been classified, and for a disturbance of 1/6, the optimal incoherent eavesdropping strategy reduces to the universal quantum-cloning machine.[46,47] One of the most important tasks in QKD is to prove the unconditional security of a protocol, i.e., security bounds in the case where Eve has unlimited power over the quantum channel. The unconditional security proof of the standard six-state scheme using only one-way classical communications has been presented. In this proof it was shown that the six-state scheme could be made secure up to an error rate of 12.7%.[18] Later, using the technique of two-way entanglement purification, the security proof against the most general attack has been derived. Based on this technique, it was shown that the six-state protocol could tolerate a bit error rate of 26.4%.[48] Moreover, the lower and upper bounds on the secret-key rate for six-state protocol use one-way classical communication.[15,16] The security bounds for the BB84 and the six-state protocols have been calculated using the smooth min-entropies obtained in Refs. [49] and [50]. Security bounds for the six-state protocol when implemented with finite resources under one-way post processing have been shown in Ref. [51]. An eavesdropping technique for the six-state protocol when Alice deliberately adds noise to the signal states before they leave her lab or in a realistic scenario where Eve cannot replace the noisy quantum channel by a noiseless one has been presented. It was found that addition of quantum noise makes quantum key distribution more robust against eavesdropping.[52]
The collective noise assumption states that if several qubits are transmitted simultaneously or they are close to each other spatially, the random unitaries or transformations of the noise on each qubit must be identical.[53] Various protocols have been studied under collective noise.[31,35–37] Recently, studies on the effect of counter-clockwise and clockwise collective-rotation noise on the security of quantum key distribution have been reported in Refs. [54] and [55], respectively. We analyze the effect of clockwise collective-rotation noise in the channel represented by the following unitary rotation matrix:
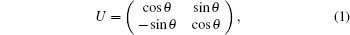
Collective rotation noise transforms the six states in the protocol as follows:
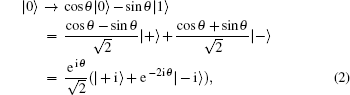
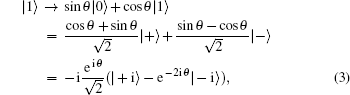
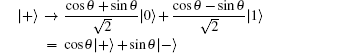

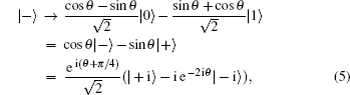
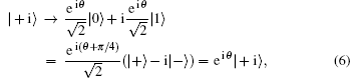

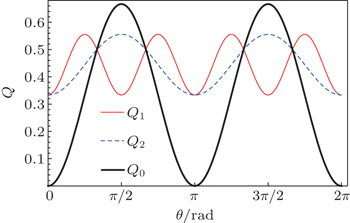
Collective-rotation noise introduces bit-flip errors in the {|0〉, |1〉} and {|+〉, |−〉} bases, and phase in the {| + i〉,| − i〉} basis. The weighted sum of the bit-flip errors gives the quantum bit error rate, which can be defined as the probability that a randomly selected qubit sent by Alice arrives flipped, that is, |0〉 as |1〉, |+〉 as |−〉, | + i〉 as | − i〉 and vice versa. According to Eqs. (

The QBER is an important parameter in quantum cryptography, it is used to investigate the security of QKD protocols. The QBER gives the ratio of signals for which Alice and Bob chose the same encoding but where Bob got a measurement outcome different from what Alice prepared.[2] It is customary to define a parameter ɛ = Q0 as the channel noise level.[25] We, however, choose not to attach any operational definition but rather use ɛ = Q0 = 2/3sin2θ to simplify expressions whenever it is convenient to do so. We note the periodic nature of Q0.
To perform an intercept-resend attack,[56] Eve randomly measures qubits sent by Alice in any one of the three bases. She then forwards, to Bob, qubits prepared in states corresponding to her measurement outcomes.[2] Given an ordered set S = {|0〉,|1〉,|+〉,|−〉,| + i〉,| − i〉} of the possible states of the qubits, the effect of Eve’s actions can be represented by the following probability transition matrix:
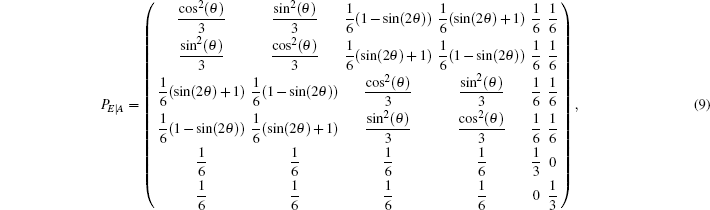
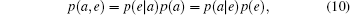
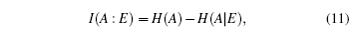
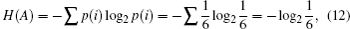
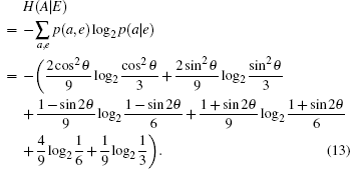
| Table 2. Summary of joint probabilities of Alice preparing certain states and Eve obtaining measurement outcomes corresponding to each of the six states on qubits sent by Alice. . |
To simplify Eq. (

 | Fig. 2. Variation of the mutual information between Alice and Eve (I(A : E)) as a function of the collective-rotation angle θ. |
We analyze the following two intercept-resend strategies that could be employed by Eve.
Eve breaks the quantum channel between Alice and Bob and inserts both of her devices in between, as illustrated in Fig. Eve places her preparation device at a location close to, possibly inside, Bob’s lab and connects her measurement and preparation devices by a lossless classical channel,[56] as illustrated in Fig.
The transition probability matrices describing the transition between the states prepared by Eve and the states obtained by Bob are given by
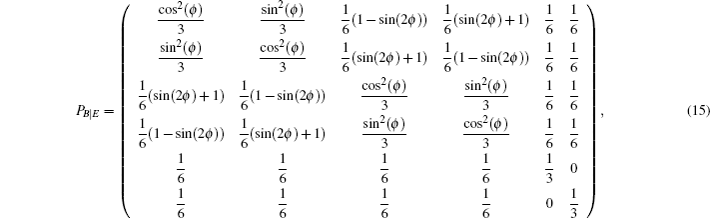
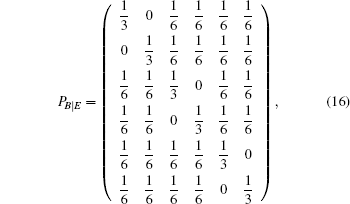
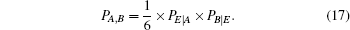
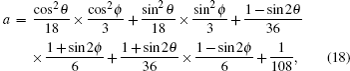

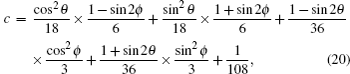
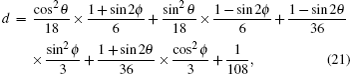
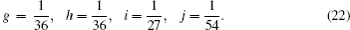
| Table 3. Summary of the joint probabilities of Alice preparing certain states and Bob obtaining measurement outcomes corresponding to each of the six states, given an intercept-resent attack by Eve. . |
The terms c, d, g, and h in Table
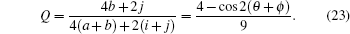
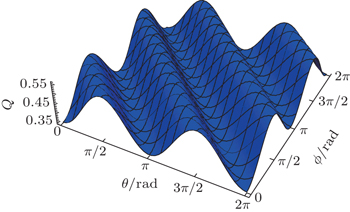
The variation of the quantum bit error rate Q with rotation angles θ and ϕ is shown in Fig.
In the special case where θ = ϕ, i.e., the noise in both channels is equal, the quantum bit error rate Q reduces to
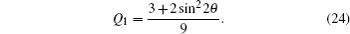
By performing an attack outlined in strategy (II), Eve attempts to minimise her quantum “footprint" by substituting collective-rotation noise channel with a lossless classical channel. It turns out that the strategy does not improve her odds of not being detected, as shown in Fig.
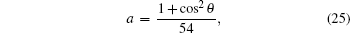
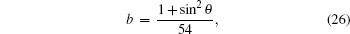
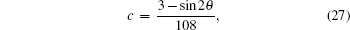
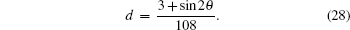
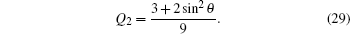
Alice and Bob attribute quantum bit error rate above a predetermined value to eavesdropping. From Fig.

We have demonstrated how the six-state QKD protocol responds to collective-rotation noise. From the analysis, we note that the six-state protocol is robust against collective-rotation noise for small rotation angles. We attribute this result to the symmetry of the protocol. We also note that the third basis {| + i〉,| − i〉} is rotation invariant under collective-rotation noise thus reducing the quantum bit error rate. We recommend the six-state protocol for QKD implementations where collective-rotation noise is dominant in the communication channel.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 |