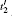† Corresponding author. E-mail:
Project supported by Special Funds for Scientific and Technological Innovation Projects in Tianjin, China (Grant No. 10FDZDGX00400) and the Tianjin Research Program of Application Foundation and Advanced Technology, China (Grant No. 15JCQNJC01100).
We investigate the intensity and efficiency of a compressed echo, which is important in arbitrary waveform generation (AWG). A new model of compressed echo is proposed based on the optical Bloch equations, which exposes much more detailed parameters than the conventional model, such as the time delay of the chirp lasers, the nature of the rare-earth-ion-doped crystal, etc. According to the novel model of compressed echo, we find that reducing the time delay of the chirp lasers and scanning the lasers around the center frequency of the inhomogeneously broadened spectrum, while utilizing a crystal with larger coherence time and excitation lifetime can improve the compressed echo’s intensity and efficiency. The theoretical analysis is validated by numerical simulations.
The three-pulse photon echo (3PE) is a well-known technique which is applied to arbitrary waveform generation (AWG) and stores intense light pulses by a rare-earth-ion-doped crystal (REIC).[1–4] Compared to the traditional waveform generation methods, this AWG technology enjoys unrivaled capabilities in terms of processing bandwidth and time-to-bandwidth product (TBP). According to the 3PE mechanism, the compressed echo sequences are generated by REIC and can be controlled to change their shapes by adjusting the chirp lasers, thus forming AWG. This technique can generate ∼GHz/s bit rate codes with fantastic ∼105 TBP, such as an ASC-II code,[5] a periodic Barker code,[6,7] and a pulse-position-modulation code.[8] Several successful cases of AWG based on the 3PE technology have been demonstrated. Meanwhile research for the improvements of 3PE’s intensity and efficiency is continuing.
In most previous papers, the stimulated 3PE response is extensively written as the convolution product of the three input pulses’ driving fields (Eq. (
In this paper, we consider the REIC as a thin medium and present a theoretical model for compressed echo generation in a two-level system by using the optical Bloch equations. The compressed echo can be regarded as the aggregation of numerous single photon echoes which occur from fs1 to fs1 + B.[2,4] Therefore, we first deduce the expression of a single photon echo and verify that the larger time delay of the input pulses will decrease the echo’s intensity. Furthermore, the efficiency of the photon echo is a sine-like function with the increase of the rephasing pulse’s area and optical thickness. Then, we establish the relationship between the single photon echo and the compressed echo. Compared with the conventional model of compressed echo, the novel model exposes much more detailed parameters which can be controlled in practice. According to the novel model of compressed echo, reducing the time delay of the chirp lasers and the scanning lasers around the center frequency of the inhomogeneously broadened spectrum while utilizing the crystal with larger coherence time and excitation lifetime can improve the intensity and efficiency of the compressed echo, which makes the 3PE technology more suitable for AWG.[5–8] Finally, the theoretical analysis is validated by numerical simulations.
This section consists of two parts. We will start from the model of 3PE based on Bloch equations and analyze the factors which have influence on the echo’s intensity and efficiency. Then we will establish the relationship between 3PE and the compressed echo, and propose several methods to improve the compressed echo’s intensity and efficiency.
The coherent effect of pulses on a system of inhomogeneously broadened two-level atoms is given by Bloch’s equations, where the electric field acts as a source for the atomic dipoles.[11] The Bloch equations govern the coherent lossless interaction of light pulses and atomic dipoles, and are given as[12]



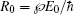
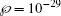
The 3PE will appear at t3PE when three laser pulses with ultrashort time width are shot into the crystal successively, as shown in Fig.
At time t1, the Bloch vectors are set as u(t1)= v(t1)= 0 and w(t1)=−1. Consider that the time width of the input pulses is far less than T1, T2, and the input pulses are strictly resonant, namely, Δ ≈ 0, thus the Bloch vectors during 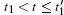

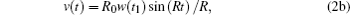
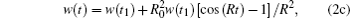
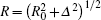
The signal field in pulse #1’s optical nutation is given by

The Bloch vectors of pulse #1 during free induction decay 


In the calculation, we note[14]

Similarly, the input pulse #2 has optical nutation and free induction decay processes as well. The Bloch vectors during 


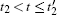



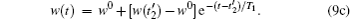
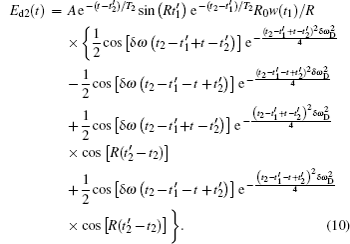
The third input pulse #3 has the same processes as the former two. During the optical nutation process, namely, 




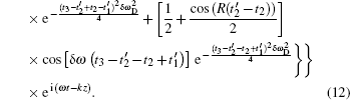
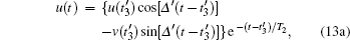


The photon echo will appear at time 
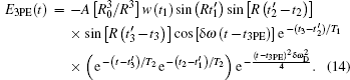

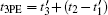

Assume that the time width of each input pulse is 5 ns, which is much shorter than the population lifetime T1 and the coherence time T2. As shown in Fig. 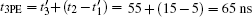
According to Eq. (

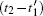

As shown in Fig.
The read out efficiency of the photon echo is easily obtained as



In Eq. (
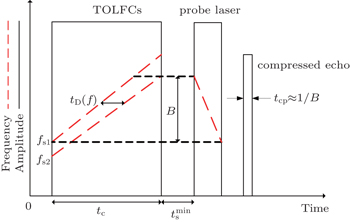
The arbitrary waveform generation based on 3PE is popularly used in optical communication and different signals’ generation. The arbitrary waveform consists of compressed echo sequences whose intensity and phase can be controlled by the chirp lasers. To achieve a compressed photon echo, three different linear chirp lasers are shot into an REIC. A spectral grating can be formed in the inhomogeneous broadened absorption profile when two temporally overlapping linear frequency chirps are overlapped within the REIC.
As shown in Fig.
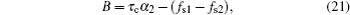
The delay time between the first two linear chirp lasers at certain frequency f can be given as

After the spectral grating is produced and delay time τs, a probe laser scans the REIC with chirp rate α3 = (α1 α2)/(α2 − α1). Due to the compression effect of the chirp lasers, a pulse compression echo τcp ≈ 1/B appears.
The compressed echo can be regarded as the aggregation of numerous single photon echoes which occur from fs1 to fs1 + B,[2,4] but it has no explicit expression in the previous papers. Therefore, we are interested in finding a mathematical expression describing the relationship between the single photon echo and the compressed echo.
According to Fig.
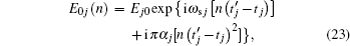
 | Fig. 6. Diagram for generation of compressed echo. Each chirp laser is regarded as numerous discrete frequency rectangle pulses, where N is the amount of pulses and Δ ω is the frequency step. |
Therefore, the model of the compressed echo can be written as

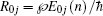

The simulation is performed to demonstrate the compressed echo which is the aggregation of numerous single photon echoes with different frequencies. All the parameters used are cited from Ref. [3]. The population lifetime T1 is set as 10 ms and the coherence time T2 = 150 μs. The inhomogeneous width δωD is set as 40 GHz and the thickness of the medium L = 2.5 mm. The grating bandwidth B is set as 1.2 GHz and the amount of discrete number N = 1.2× 109, namely, the frequency step Δω = 1 Hz. The start frequency ωs1 is set as 80 MHz and the frequency shift δω is set as 50 MHz. The durations of the three chirp lasers are 800 μs, 788.7 μs, and 12 μs, respectively. The chirp rate of each laser should follow α3 = (α1 α2)/(α2 − α1), namely,
The minimum time delay 
 | Fig. 7. Simulation of compressed echo whose full width at half magnitude (FWHM) is 1 ns. The time width τcp of the compressed echo is obviously narrow, which approaches the theoretical value 1/B ≈ 0.83 ns. Our simulation result is quite close to the experiment result (FWHM is 0.9 ns) in Ref. [3]. |
Meanwhile, we can calculate the intensity and efficiency of the compressed echo in Ref. [3]. They used yttrium orthosilicate (Er3+:YSO) crystal (T2 ∼ 150 μs and T1∼ 11 ms) to produce the compressed echo. The time delay at the same frequency τD(f) is set as 11.3–12.42 μs, while the minimum time delay 

Now, we propose some approaches for improving the intensity and efficiency of the compressed echo in arbitrary waveform generation based on Eqs. (
The first method is controlling the time delay τD. Equation (

As shown in Figs.
Another method is to reduce the time delay 
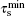

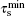
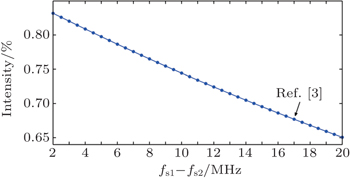 | Fig. 8. Relationship between difference of start frequency (fs1–fs2) and compressed echo’s intensity. |
As shown in Fig. 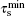
Increasing the optical thickness is also a useful method. According to Eq. (
It is unpractical to replace a much thicker REIC in the cryogenic equipment frequently. Thus, it is reasonable to increase the absorption coefficient α and it can be expressed as[12]

The proper choice of REIC is also necessary. Different rare-earth-ion-doped crystals possess different T2 and T1. The coherence time T2 is determined by T2 = 1/(π Γh), where Γh is the homogeneous width of the medium. With the decrease of the temperature (ultralow temperature of 3–4 K), the line shape of the homogeneous broadening becomes sharper, which makes Γh narrower and enhances T2 at the same time.[16,17] The population lifetime T1 is decided by the wavelength of the excited state in the two-level system. According to Eq. (
Take the case in Ref. [3] for example; if we replace Er3+:YSO with Tm3+:YAG (T2 ∼ 20 μs and T1∼ 10 ms) and do not change other parameters, we will find that the intensity and efficiency of the compressed echo are 7.9% and 8%, respectively, which are far smaller than those with the Er3+:YSO crystal.
Larger coherence time T2 and excitation lifetime T1 may reduce the efficiency of 3PE, but they can lead to a higher intensity that offsets the increase of e−αL. Therefore, the crystal with larger coherence time T2 and excitation lifetime T1 is beneficial to produce the compressed echo, which will be more suitable for the arbitrary waveform generation and optical storage based on the 3PE technology.[3,5]
We have proposed a novel model of compressed echo. We first deduced the expression of 3PE based on the Bloch equations and verified that larger time delay of the input pulses will decrease the echo’s intensity. Furthermore, the efficiency of 3PE is a sine-like function with the increase of the rephasing pulse’s area and that of the optical thickness. Then, we gave the relationship between the single photon echo and the compressed echo. The novel model of compressed echo predicts the possibility of achieving high intensity and efficiency of the compressed echo. According to this model, we gave several suggestions for improving the compressed echo. These results and recent results of echoes in inverted media serve as a motive to further study the possibility of obtaining a highly efficient and strong echo.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 |