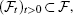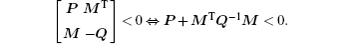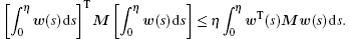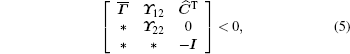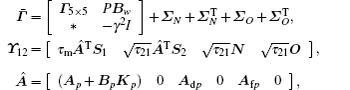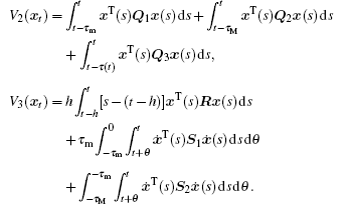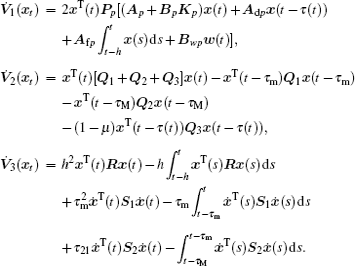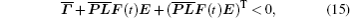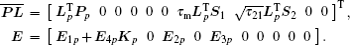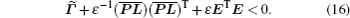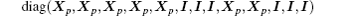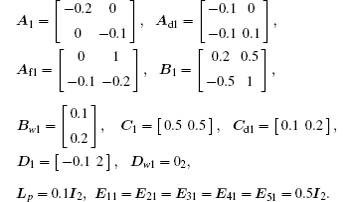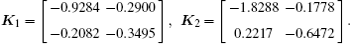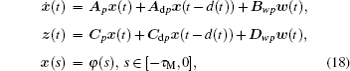Department of Mathematics, Thiruvalluvar University, Vellore-632115, Tamil Nadu, India
† Corresponding author. E-mail: saravanamaths30@gmail.com
‡ Corresponding author. E-mail: syedgru@gmail.com
Project supported by Department of Science and Technology (DST) under research project No. SR/FTP/MS-039/2011.
1. IntroductionTime delays are frequently encountered in many practical systems. They are common in many industrial and engineering systems such as communication networks, manufacturing devices, and biology. Since the system stability is an essential requirement in many applications, much effort has been devoted to investigate the stability criteria for various time-delay systems during the last few decades.[1–4] It is well recognized that the presence of time delay in a dynamical system is often a primary source of instability and performance degradation. Moreover, the delay-dependent[5] results are generally less conservative than the delay-independent ones,[6] especially when the delay is small. Recently, much attention has been paid to the robust stability problem for uncertain systems with time delays.[7,8]
Markovian jump systems are a special sort of hybrid system, which are driven by a Markov chain, where they may undergo unexpected changes in their structures and parameters, e.g., aerospace systems, power systems, etc.[9–11] Such systems can be described by a set of time-delayed linear systems with the transitions between models determined by a Markov chain in a finite mode set. Applications of this class of systems may be found in processes including those in production systems and economic problems, etc. In the last few years, some quite significant results on the stability analysis and controller synthesis for Markovian jumping systems with time-delay have been reported.[11,12]
The control design for uncertain systems with time-varying delays has been a difficult problem of control theory.[13,14] Theoretically, this issue could be solved by the Lyapunov method. The H∞ performance is usually analyzed in the control theory to synthesize controllers achieving stabilization with guaranteed performance. Stability is one of the most important problems in the synthesis of control systems. Therefore, the problems of delay-dependent stability analysis and H∞ control for delayed systems have received substantial attention among the control community for the last few decades.[15]
The H∞ control concept was proposed to reduce the effect of the disturbance input on the regulated output within a prescribed level and guarantee that the closed-loop system is stable. In Refs. [16] and [17], the H∞ technology was proposed to solve the disturbance attenuation problem in various difficult systems. In this paper, we provide a delay-dependent H∞ control for Markovian jump uncertain systems with interval time-varying and distributed delays. A linear matrix inequality (LMI) optimization approach is used to achieve the best effect of disturbance attenuation. The obtained results in this paper are generally less conservative than those of some existing methods.
The following notations are used. Throughout this paper, ℝn and ℝn×n denote the n-dimensional Euclidean space and the set of all n × n real matrices, respectively. For a matrix B and two symmetric matrices A and C,  denotes a symmetric matrix, where the notation * represents the entries implied by symmetry. AT and A–1 are the matrix transpose and inverse of A, respectively. X > 0 means that matrix X is a symmetric positive definite matrix with appropriate dimensions. I denotes the identity matrix with appropriate dimensions. ε denotes the expectation operator with respect to some probability measure
denotes a symmetric matrix, where the notation * represents the entries implied by symmetry. AT and A–1 are the matrix transpose and inverse of A, respectively. X > 0 means that matrix X is a symmetric positive definite matrix with appropriate dimensions. I denotes the identity matrix with appropriate dimensions. ε denotes the expectation operator with respect to some probability measure  . Let
. Let  be a complete probability space which relates to an increasing family
be a complete probability space which relates to an increasing family  of σ algebras
of σ algebras 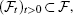 where Ω is the sample space,
where Ω is the sample space, 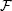 is the σ algebra of subsets of the sample space, and
is the σ algebra of subsets of the sample space, and  is the probability measure on
is the probability measure on 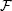 . Let
. Let  f(t) ∈ L2[0,∞), ||f|| refers to the Euclidean norm of function f(t) at time t.
f(t) ∈ L2[0,∞), ||f|| refers to the Euclidean norm of function f(t) at time t.  is the space of square integrable vectors on [0,∞).
is the space of square integrable vectors on [0,∞).
2. Problem statementLet {rt,t ≥ 0} be a right-continuous Markov chain on a probability space  taking values in a finite state space
taking values in a finite state space  with generator Π = {πpq} given by
with generator Π = {πpq} given by

where
Δ > 0,

and
πpq ≥ 0 is the transition rate from
p to
q if
q ≠
p, while

Consider the following uncertain Markovian jump system with interval time-varying and distributed delays:

where
x(
t) ∈ ℝ
n is the state,
u(
t) ∈ ℝ
m is the control input,
w(
t) ∈ ℝ
p is the disturbance input which belongs to
L2[0,∞), and
z(
t) ∈ ℝ
q is the controlled output of the system. The initial vector
ϕ ∈
C0, where
C0 is the set of continuous functions from [–
τM, 0] to ℝ
n.
τ(
t) and
h denote the time-varying delay and the distributed delay, respectively, and
τ(
t) is assumed to satisfy

where
τm,
τM,
h, and
μ are constants. The matrices
A(
rt,
t) =
A(
rt) + Δ
A(
rt,
t),
Ad(
rt,
t) =
Ad(
rt) + Δ
Ad(
rt,
t),
Af(
rt,
t) =
Af(
rt) + Δ
Af(
rt,
t),
B(
rt,
t) =
B(
rt) + Δ
B(
rt,
t), where
Bw(
rt),
C(
rt),
Cd(
rt),
D(
rt) are known real constant matrices with appropriate dimensions, and Δ
A(
rt,
t),Δ
Ad(
rt,
t), Δ
Af(
rt,
t), Δ
B(
rt,
t) are real-valued unknown matrices representing the time-varying parameter uncertainties which are assumed to be of the following form:

where
L(
rt) and
Ei(
rt) (
i = 1,2,3,4) are known real constant matrices and
F(
t) is an unknown time-varying matrix function satisfying
FT(
t)
F(
t) ≤
I, ∀
t. Since almost every sample path of the above Markov chain is a right-continuous step function with a finite number of simple jumps, the global existence results on the solutions of the Markovian jump system (
1) can be found in Section 4 of Ref. [
20].
Lemma 1 (Schur complement[18]) Let M, P, Q be given matrices and Q > 0, then
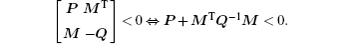
Lemma 2[18] For any constant matrix M ∈ ℝn × n, M = MT > 0, scalar η > 0, vector function w: [0, η] → ℝn such that the integrations concerned are well defined,
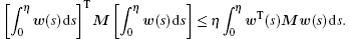
Lemma 3[19] Let D, E, and F(t) be real matrices of appropriate dimensions, and F(t) satisfies FT(t) F(t) ≤ I, then the following inequality holds for any constant ε > 0:

3. Main resultsFor the sake of notation simplification, in the following, for each possible rt = p (p = 1,2,…,m), we simply write L(rt) as Li; for instance, A(rt,t) is denoted by Ap(t), and Ad(rt,t) by Adp, and so on. On the other hand, we have u(rt) = up(t). We now rewrite system (1) by using state feedback control up(t) = Kpx(t) as follows:

Theorem 1 For a prescribed scalar γ > 0 and some given positive scalars τm, τM, h, μ and matrix K, system (4) with condition (2) is asymptotically stable and satisfies ||z(t)||2 ≤ γ||w(t)||2 for all nonzero  if there exist matrices Pp > 0, Qi > 0 (i = 1,2,3), R > 0, Sj > 0 (j = 1,2), and appropriate dimension matrices Nl, Ol (l = 1,2,3,4,5) such that the following LMI is satisfied:
if there exist matrices Pp > 0, Qi > 0 (i = 1,2,3), R > 0, Sj > 0 (j = 1,2), and appropriate dimension matrices Nl, Ol (l = 1,2,3,4,5) such that the following LMI is satisfied:
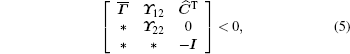
where
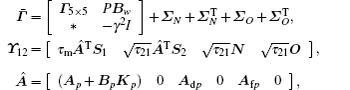

Proof Define the Lyapunov functional candidate as

where

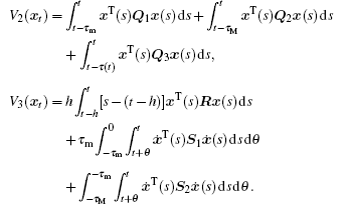
By calculating the time derivative of
V(
xt) along the trajectories of system (
4), we obtain

where



From Eq. (
6),
V̇1(
xt),
V̇2(
xt), and
V̇3(
xt) are calculated as follows:
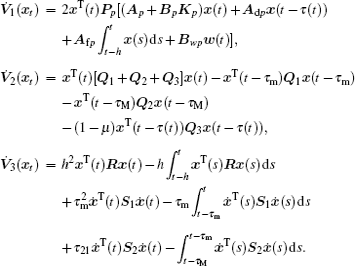
By applying Jensen’s inequality, we obtain



Substituting Eqs. (8)–(11) into Eq. (7), we obtain

where

Under the zero initial conditions and
V(
x(
t))|
t=∞ → 0 for system (
4), we obtain


By using Lemma 2,
Γ̃ is equivalent to inequality (
5), which means that ||
z||
2 ≤
γ||
w||
2 is satisfied for any nonzero
w(
t) ∈
L2[0,∞), which ensures the asymptotical stability of system (
4).
Theorem 2 For a prescribed scalar γ > 0 and some given positive scalars τm, τM, u, h and matrix K, system (4) with condition (2) is robustly asymptotically stable and satisfies ||z(t)||2 ≤ γ||w(t)||2 for all nonzero  if there are matrices Pp > 0, Qi > 0 (i = 1,2,3), R > 0, Sj > 0 (j = 1,2), and appropriate dimension matrices Nl, Ol (l = 1,2,3,4,5), and a scalar εp > 0 such that the following LMI is satisfied:
if there are matrices Pp > 0, Qi > 0 (i = 1,2,3), R > 0, Sj > 0 (j = 1,2), and appropriate dimension matrices Nl, Ol (l = 1,2,3,4,5), and a scalar εp > 0 such that the following LMI is satisfied:

where

Proof Replace Ap, Adp, Afp, and Bp in LMI (5) by Ap + ΔAp(t), Adp + ΔAdp(t), Afp + ΔAfp(t), and Bp + ΔBp(t), respectively, we obtain
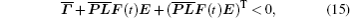
where
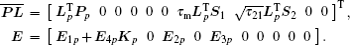
By Lemma 3, we know that LMI (
15) is equivalent to
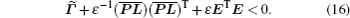
Obviously, by applying Schur complement, LMI (
16) is equivalent to LMI (
14).
Theorem 3 For a prescribed scalar γ > 0 and some given positive scalars τm,τM,u,h, system (4) with condition (2) is robustly asymptotically stable and satisfies ||z(t)||2 ≤ γ||w(t)||2 for all nonzero  if there are matrices Q̄i > 0 (i = 1,2,3), R > 0, Sj > 0 (j = 1,2), Xp > 0, Yp, appropriate dimension matrices Nl, Ol (l = 1,2,3,4,5), and a scalar εp > 0 such that the following LMI is satisfied:
if there are matrices Q̄i > 0 (i = 1,2,3), R > 0, Sj > 0 (j = 1,2), Xp > 0, Yp, appropriate dimension matrices Nl, Ol (l = 1,2,3,4,5), and a scalar εp > 0 such that the following LMI is satisfied:

where


The feedback gain matrix is given by

Proof We define

Then pre and post multiplying LMI (
14) by
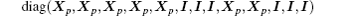
and

we can obtain LMI (
17).
4. Numerical examplesIn this section, some numerical examples are provided to demonstrate that the method proposed in this paper is effective and less conservative than some existing methods.
Example 1 Consider system (1) with the following matrix parameters.
Mode 1:
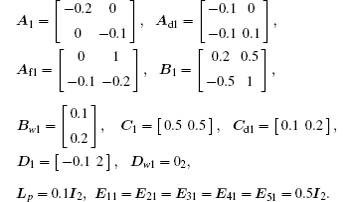
Mode 2:

In order to design a robust delay-dependent
H∞ state-feedback control, taking
τm = 0.5,
τM = 1.5,
h = 0.3, and
μ = 0.5, applying Theorem 3 in MATLAB LMI control toolbox, we obtain
γ = 0.9845,
ε1 = 1.2354,
ε2 = 1.6524, and the desired state feedback controller as follows:
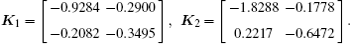
Therefore, the system of interest is robustly asymptotically stable.
Example 2 Consider the following time delay system with system mode p = 1:
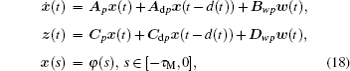
with matrix parameters in Ref. [
7]

Taking parameters h = 0 and unknown μ, and using LMI in Theorem 1, we obtain the minimum allowable H∞ performance γ for different values of τM and τm as shown in Table 1, which clearly shows that the results of the proposed method in this paper are significantly better than those in Refs. [7] and [8].
Table 1.
Table 1.
 Table 1. Example 4: minimized H∞ performance for different τM and τm. .
| Method |
τM = 0.8695 |
|
τM = 1 |
|
|
τm = 0 |
τm = 0.5695 |
τm = 0 |
τm = 0.5 |
| Ref. [7] |
0.87 |
0.81 |
4.05 |
3.27 |
| Ref. [8] |
0.81 |
0.72 |
2.95 |
2.13 |
| Thm 3 |
0.5614 |
0.5305 |
1.7458 |
1.1254 |
| Table 1. Example 4: minimized H∞ performance for different τM and τm. . |
Example 3 Consider system (18) with the following matrix parameters in Ref. [9]:

Taking parameters
τm =
h = 0 and using LMI in Theorem 1, we obtain the maximum admissible delay upper bound
τM or different values of
γ as shown in Table
2, which clearly shows that the result of the proposed method in this paper are significantly better than those in Refs. [
9] and [
10].
Table 2.
Table 2.
 Table 2. Example 4: τM and γ. .
| Method |
μ |
0.5 |
1.0 |
1.5 |
2.0 |
| Ref. [9] |
0 |
0.47 |
0.52 |
0.55 |
0.56 |
| Thm 3 |
|
0.60 |
0.64 |
0.67 |
0.69 |
| Ref. [10] |
0.5 |
0.3666 |
0.4293 |
0.4450 |
0.4524 |
| Thm 3 |
|
0.5355 |
0.5754 |
0.5863 |
0.5898 |
| Table 2. Example 4: τM and γ. . |
5. ConclusionWe have studied the H∞ control problem for systems with interval time-varying and distributed delays. On the basis of the Lyapunov functional, a delay-dependent H∞ control scheme is presented in terms of LMIs. It is shown that a desired state feedback controller can be constructed when the given LMIs are feasible, and it leads to less conservative results than the existing methods. Finally, numerical examples are given to illustrate the effectiveness of the proposed method. We are interested to extend this work to the discrete-time uncertain stochastic systems with discrete interval and distributed time-varying delays. The results will be obtained in the future.