Cite this Article
Shen Yi, Ren Gang, Liu Yang, Xu Jia-Li. A local fuzzy method based on “p-strong” community for detecting communities in networks. Chinese Physics B, 2016, 25(6): 068901  
Permissions
A local fuzzy method based on “p-strong” community for detecting communities in networks
Shen Yi1, 2, Ren Gang1, †, , Liu Yang2, Xu Jia-Li2
School of Transportation, Southeast University, Nanjing 210096, China
College of Information Science and Technology, Nanjing Agricultural University, Nanjing 210095, China

 

† Corresponding author. E-mail: rengang@seu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 51278101 and 51578149), the Science and Technology Program of Ministry of Transport of China (Grant No. 2015318J33080), the Jiangsu Provincial Post-doctoral Science Foundation, China (Grant No. 1501046B), and the Fundamental Research Funds for the Central Universities, China (Grant No. Y0201500219).

Abstract
Abstract

In this paper, we propose a local fuzzy method based on the idea of “p-strong” community to detect the disjoint and overlapping communities in networks. In the method, a refined agglomeration rule is designed for agglomerating nodes into local communities, and the overlapping nodes are detected based on the idea of making each community strong. We propose a contribution coefficient 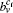to measure the contribution of an overlapping node to each of its belonging communities, and the fuzzy coefficients of the overlapping node can be obtained by normalizing the to all its belonging communities. The running time of our method is analyzed and varies linearly with network size. We investigate our method on the computer-generated networks and real networks. The testing results indicate that the accuracy of our method in detecting disjoint communities is higher than those of the existing local methods and our method is efficient for detecting the overlapping nodes with fuzzy coefficients. Furthermore, the local optimizing scheme used in our method allows us to partly solve the resolution problem of the global modularity.

PACS: 89.75.Hc;05.45.Xt
Keyword:networks;local fuzzy method;overlapping communities;fuzzy coefficients
1. Introduction

Real systems and networks such as the World Wide Web (WWW),[1] collaboration networks,[2] metabolic networks,[3] etc., are far from being purely random, within which the distribution of link density is inhomogeneous both locally and globally. This leads to a most significant property in them, that is, community or modular structure. This property allows us to have an in-depth insight into real systems and obtain more useful statistical information than on simple nodes. So far, based on the inhomogeneous distribution of connections in real networks, a widely accepted definition of communities is that communities are the groups of nodes such that the connections in the same group are denser than between groups.[4] The importance of the community identification task has been addressed in many research fields. For example, in protein–protein interaction networks, the proteins with a similar functionality tend to be observed in similar chemical reactions. In parallel computing, how to allocate tasks to processors to minimize communication cost is remarkably important.

In the past several years, many approaches have been proposed for community detection.[5–8] These approaches can be classified as several categories,[5,6] such as divisive algorithms, optimization methods, dynamic algorithms, etc. Among these methods, the methods based on the optimization of the modularity function Q[4] usually have the highest accuracy[5] because the modularity function Q is proposed based on the definition of communities. It is known that the Q is a global function and the corresponding method based on optimizing it must be a global method. Before using these optimizing methods, we need to know the topology of the whole network in advance. However, for some large and dynamic real networks such as the Internet or WWW, it is difficult to obtain their global topology knowledge since they evolve very quickly.[7] Therefore, a practical way may be local methods, and by which, a particular community starting with an initial node in a network can be discovered. Recently, several researches focused on designing efficient local methods, such as the Clauset[9] method and the Bagrow[10] method. Other local or semi-local methods that rely on a priori network assumption have been proposed,[11–13] and they are accurate only when used as a part of the global method.[10] They are Luo, Wang, and Promislow (LWP),[11] the Flake and Lawrence method,[12] Bollt method,[13] etc. Among these methods, the Bagrow method has the highest accuracy and the lowest computational cost.[10] It is worth noting that the above local methods aim to identify disjoint communities.[5] In fact, a real network is usually composed of several communities with nodes overlapping with each other, and these communities and nodes are called overlapping communities and nodes,[13] respectively. Currently, the overlapping community detection methods are mainly categorized into two types: crisp and fuzzy.[5] For crisp overlapping communities, each node belongs to one or more communities with equal strength.[5] For a fuzzy overlapping community, each node belongs to more than one community with different strengths.[5] The belonging coefficients or fuzzy coefficients measure how an overlapping node is distributed among different communities. The value of the belonging coefficient is between 0 and 1 representing the strength of membership of a node v to a community. Meanwhile, for node v, the sum of belonging coefficients for all communities is 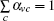. Unlike the crisp clustering that can only find the overlapping nodes or communities, fuzzy clustering has provided detailed belonging coefficients that help us to understand in depth the intercourses within the networks. Recently, many efficient fuzzy methods have been proposed.[14–17] For example, the spectral and fuzzy c-means,[15] the distance matrix-based fuzzy method,[16] the Bayesian nonnegative matrix factorization (NMF),[17] etc. The above methods are global methods, and some of them need to know the number of communities at first and obtaining belonging coefficients is of high cost.[5,18,19]

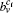
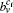
In this paper, we propose a local method to detect the disjoint and overlapping communities. The method is based on the idea of “p-strong” community. In the method, a refined agglomeration rule is designed for agglomerating nodes into local communities accurately, and the overlapping nodes are detected based on the idea of making each community strong. We propose a coefficient to evaluate the contribution of node v to the community Ci, and the overlapping nodes with belonging coefficients are obtained by normalizing the to all its belonging communities. The running time of our method is analyzed and varies linearly with network size. We apply our method to the computer-generated networks and real networks. The results show that our method performs in detecting disjoint communities better than the Clauset[9] method and the Bagrow[10] method. For the detection of overlapping nodes with belonging coefficients, our method has lower cost than many existing global fuzzy methods. Furthermore, due to the local optimizing scheme, our method can partly solve the resolution problem of the global modularity.[20]

2. Algorithm
2.1. Main idea of the local methods

Before presenting our method, it is necessary to present the main idea of several existing local methods, such as the Clauset method[9] and the Bagrow method,[10] which can help to understand the implementation and advantages of our method we presented in Subsection 2.2.

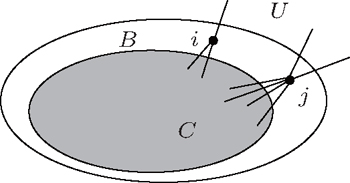
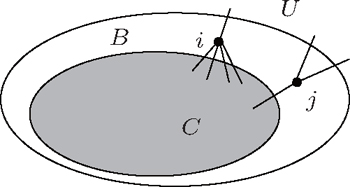For a network, the two local methods divide it into three parts, i.e., the detected community C including a starting node, the region B in which all nodes have neighbors in C, and the region U that is unknown, as figure 1 shows. Initially, the detected community C includes only a starting node. Then, one or more nodes in B will be chosen and agglomerated into C each time. At the same time, B is updated by putting the outside nodes in U into B, and U is also updated. This process continues until all nodes have been agglomerated. In this process, each local community is addressed by a stopping criterion.

Fig. 1. Community C surrounded by a boundary of explored nodes B which is adjacent to C. U represents the unknown potential region.

The Clauset algorithm[9] determines a local modularity for agglomerating nodes, which is rewritten by Bagrow as[10]

where βij represent those edges with one or more endpoints in Cborder, Cborder is the node inside C that has at least one neighbor in B. The value of R changes when a node in B is agglomerated into C, denoted by ΔR. At each step, we can select the node with the largest ΔR and agglomerate it into C, and the local maximal R corresponds to a local community. For a network with average degree d, the local community with size C can be detected in an average time O(|C|2d),[9] and the cost for detecting all communities increases with the number of communities and their sizes. Bagrow defines the following outwardness coefficient for a node v ∈ B from community C,[10] which is written as

where kv is the node degrees, and represent the links in and out of the detected community C, respectively. At each step, the Bagrow method agglomerates the node with the smallest Ω. For finding a local community with size C, the running time of the method is O(|C|d2log|B|), where d is an average degree of the network. For a sparse network, the cost is O(|C|log|C|)[10] since the size of |B| is similar to the size of |C|. We can see that the Bagrow method has lower cost than the Clauset method because d log |B| is usually smaller than |C|. The testing results in Ref. [10] show that the Bagrow method is more accurate than the Clauset method.

2.2. Our local community detection method

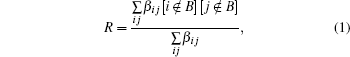
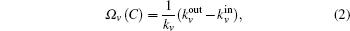
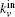
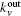
From the above, we can see the basic idea of the local community detection methods is how to agglomerate the nodes into communities. In Fig. 2 we present a simple case in which there are two nodes i and j in B. Node i has two neighbors inside C and one neighbor outside C. Node j has four neighbors inside C and two neighbors outside C. For the Bagrow method, if the two nodes have the same smallest Ω, it will be selected at random to be agglomerated into C. However, for a local method the next step of agglomeration is based on the results of its previous step of agglomeration. Therefore, the accuracy of a local method is inevitably influenced by the agglomeration steps. For this case, the question is how to determine the agglomeration sequence.

Fig. 2. Two or more nodes with the same value of kin/kout or the same smallest Ω.

We can solve the problem based on the idea of making the community strong. We use Min and Moutto denote the numbers of edges internal and external to C[21]

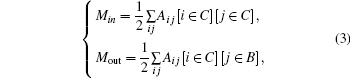
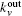
where A is the adjacent matrix with elements Ai j. If there is an edge between nodes i and j, then Ai j = 1, and Ai j = 0 otherwise. With the increase of Min/Mout, the community becomes strong because the edge density within C is larger than those outside the C. At time step t + 1, if a node v in the B with degrees and is agglomerated into the C, ΔM can be calculated as follows:

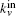
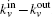
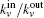
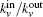
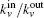
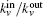
It can be seen from Eq. (4) that obtaining a more strong community corresponds to two conditions, larger and larger . In other words, if there are two or more nodes with the same kin/kout but with different degrees, we should choose the nodes with the largest kin. We present in detail the agglomeration of our method as follows.

Step 1 For each node v in the B, calculate the value of .

Step 2 Find the v with the largest and agglomerate the node into the C. If there are two or more nodes with the same largest , go to step 3.

Step 3 Find the node that has the largest kin, then agglomerate the node into the C. If there are two or more nodes with the same largest kin and , agglomerate one of them into the C at random.

This process runs until a stopping criterion is satisfied. We use the “p-strong” criterion as the stopping criterion. For a completely strong community C, each node in C has more neighbors inside than outside, which can be written as

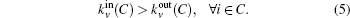
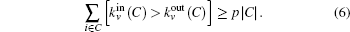
However, this condition is usually not satisfied especially for real networks. Hence, a low condition can be relied on. For a community, if only a fraction p of the nodes in C satisfy Eq. (5), we can call the community “p-strong” as described in Eq. (6). Then, we can stop agglomerating nodes if the local community stop is strong, and we have

The detected C is maintained when the community ceases to be strong. Then we can address the C by calculating the local modularity.

2.3. Detecting overlapping nodes with fuzzy coefficients

It is known that the modularity of a network can be increased if we agglomerate the overlapping nodes into their corresponding overlapping communities.[5] In other words, for an overlapping node, all its corresponding overlapping communities become “stronger” if we agglomerate the node into them respectively. However, the contributions to different overlapping communities may be different. This is in accordance with the idea of fuzzy coefficient that is used to measure the extent to which an overlapping node belongs to its overlapping community. Based on this idea, we can extend our method to detect the overlapping nodes and their overlapping communities by using the fuzzy coefficients. In the agglomerating process of our method, the overlapping nodes will be agglomerated into different overlapping communities for obtaining “stronger” communities. Therefore, after agglomerating all the nodes, the overlapping nodes can be found. In order to know the individual contribution of an overlapping node v to one of its community Ci, we can remove v from Ci and re-agglomerate it into Ci again. 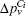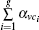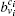Then increments of ΔMv(Ci) and the community “strong” parameter can be calculated. We propose a normalized coefficient as

to describe the contribution of an overlapping node v to a community Ci, and this coefficient is suitable for coordinating other overlapping nodes. A systematically balanced contribution of the overlapping nodes to their communities is required for making fair comparisons and helping to obtain accurate fuzzy coefficients for those overlapping nodes. In a network, we give the estimation of the fuzzy coefficients for an overlapping node v to its goverlapping communities as follows:

where the numerator represents the contribution of the node v to the overlapping community ci, and the denominator is the sum of all the contributions to all the overlapping communities. Obviously, the sum of the fuzzy coefficients of node v to all its belonging communities is 1. The detailed description of our local fuzzy method for finding the overlapping nodes with fuzzy coefficients is as follows.

Step 1 Record the nodes vi that are agglomerated into different local communities ci and increase or maintain the value p of “p -strong” for a belonging community.

Step 2 Calculate the normalized contribution of the nodes vi to each overlapping community ci, denoted by .

Step 3 Calculate the corresponding fuzzy coefficients according to Eq. (8).

2.4. Analysis of the computational complexity

In our method, the kin/kout of a node can be calculated with the knowledge of node degrees, and the cost of agglomerating |C| is O(|C|d2log|B|) for a network with average degree d. This is similar to the Bagrow method. Moreover, the cost can be written as O(|C|log|B|) for a sparse network. The overlapping nodes and their overlapping communities can be found after all the nodes have been agglomerated. The cost of obtaining the fuzzy coefficients depends on the number of the overlapping nodes and their overlapping communities. 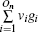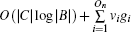For a network that has On overlapping nodes, the cost of obtaining the fuzzy coefficients is , where gi is the number of communities that node vi belongs to. Then, the total running time of our local method is linear: for finding the overlapping nodes with fuzzy coefficients and their overlapping communities.

For detecting disjoint communities, we can see that the cost of our method is linearly increasing with the augment of network size which is smaller than those of many existing methods.[5] For detecting the overlapping communities, our method has lower computation cost than many global overlapping-community detection methods and fuzzy methods.[5] Although our method cannot provide the global view of fuzzy coefficients for all the nodes in a network, the key overlapping nodes with fuzzy coefficients and their overlapping communities can be obtained quickly by our method. These overlapping nodes are very important in real networks since they usually act as key media between different functional groups,[4] such as the gateways in computer networks, the relationship coordinators in social networks, the interdisciplinary papers in citation networks, etc.

3. Simulations

In this section, we apply our method to several computer-generated networks including the Girvan and Newman (GN) networks[4] and a set of Lancichinetti, Fortunato and Radicchi (LFR) networks[22] with known community structure. Then, several real networks are investigated.

3.1. GN networks

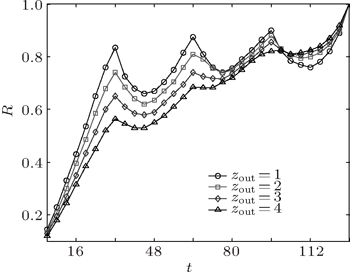
We first apply our method to the well-known GN networks[4] to show the implementation of our method. In each GN network, 128 nodes are divided into four groups. Each group has 32 nodes and each node has z = zin + zout = 16 edges, where zout is the edges that connect the nodes outside its group and zin is edges that connect the nodes inside its group[4]. We use local modularity R to show the agglomeration process. In the agglomeration process, the local modularity R changes with the number of agglomerations t. Figure 3 shows the R as a function of the number of agglomerations t, each datum point is obtained by averaging over 400 networks. We can observe that each local maximum is corresponding to a local community, and the accuracy decreases with the increase of zout.

Fig. 3. Results of our method on the GN networks.

We use the normalized mutual information (NMI)[6] to investigate the accuracy of our method. The NMI measures the difference between the true partition A and found partition B, which is written as[6]

where N is a matrix with Ni j being the number of nodes from real group i that were in found group j; CA and CB are the numbers of real communities and detected communities respectively; Ni. and N.j are the sums over row i and column j of matrix N respectively. The range of NMI is between 0 and 1. A large value of NMI corresponds to accurate community division. Figure 4 shows the results of our method on the GN networks. We also investigate the Clauset method and Bagrow method on the networks for comparison. From Fig. 4 we can see that the three methods perform well for small values of zout. The accuracy for each of all the methods decreases with the increase of zout. With the increase of zout, we observe that our method performs best among them. The results show that the refined choosing strategy employed in our method can increase the accuracy of our method.

Fig. 4. Results on the GN networks each as a function of zout, each datum point is obtained by averaging over 400 networks.
3.2. LFR networks

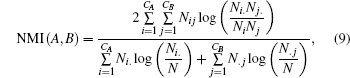
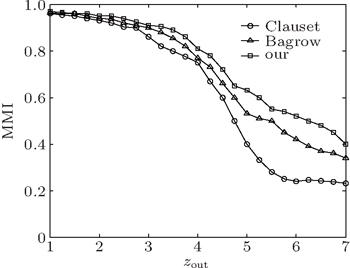
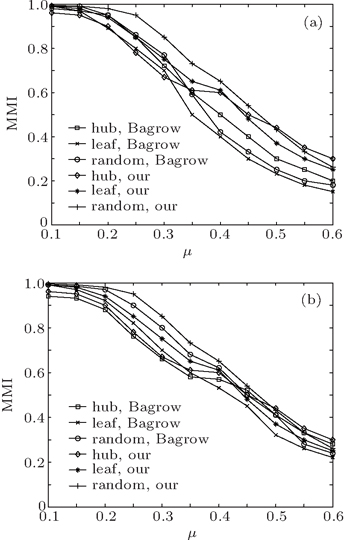
The topology of GN networks is unrealistic since real networks show heterogeneous distributions of community sizes and node degrees. In this subsection, we use a set of realistic benchmark networks called LFR benchmark networks[22] to test our method. The LFR networks have heterogeneous degree distributions and community sizes, and allow communities to overlap, which are in accordance with the features of real networks, and have been widely used for testing the community detection methods in recent years.[5,23–26] The adjustable topology parameters for the LFR benchmark networks are network size N, average degrees ⟨k⟩, maximum degrees kmax, minimum and maximum community size cmin and cmax, the degree distributions γ, the community size distributions β, the mixing parameter μ, the number of communities each overlapping node belongs to om, and the number of overlapping nodes on.[22] In order to detect the overlapping communities and nodes and make comparisons with other well-known fuzzy overlapping community detection methods, such as Fuzzyclust[27] and NMF,[17] we first investigate our method on the LFR networks without overlapping nodes to compare with the existing local methods in the detection of disjoint communities. The LFR networks have the mixing parameter μ in a range from 0.1 to 0.6, ⟨k⟩ = 24, cmin = 16, and cmax = 64, γ = 2.5, β = 1.5, and N = 500. We start our method on the leaf nodes, hub nodes, and randomly selected nodes separately. In Fig. 5 we show the results of the Clauset method, the Bagrow method, and our method, on the LFR networks. For clarity, we show the comparisons between our method and the other two methods in Figs. 5(a) and 5(b) respectively.

Fig. 5. Results measured by NMI on the LFR networks, in which each datum point is obtained by averaging over 400 networks, showing the comparisons of the results from our method with the results from (a) the Clauset method and (b) the Bagrow method.

From Fig. 5 we can see that for low value of mixing parameter the accuracies of the three methods are all high. With the increase of the μ value, the network becomes confused and is difficult to identify. We can see from Figs. 5(a) and 5(b) that if the starting node is a leaf node or a node randomly selected, the accuracy of our method is higher than the other two methods almost until μ reaches 0.6. For μ ≤ 0.3, when the starting node is a hub node, the accuracy of the Clauset method is higher than that of our method. In really large networks, a hub node or leaf node is difficult to identify. So, our method has the advantages in accuracy since the starting node is selected at random, i.e., averagely.

Next, we compare our method in detecting the overlapping nodes and their belonging coefficients. We generate the LFR networks with the mixing parameters μ = 0.1 and μ = 0.3, and the ratio of overlapping nodes on/N ranging from 0 to 1, and om = 2 for on/N > 0. The rest of the parameters have been presented above. We use the fuzzy Rand index (FRI) measure (named after William M. Rand)[6] to quantitatively compare the known-fuzzy division with the fuzzy division obtained by our method. Figure 6 shows the FRI as a function of ratio of overlapping nodes denoted by fp. From Fig. 6, we can see that our method performs well and its performance is close to those of the other two methods for the most cases. The two referenced methods have high computation complexities: O(kdn2)[27] for the Fuzzyclust and O(kn2)[17] for the NMF, where d is the number of iterations leading to convergence, while the computation cost of our method is much lower than those of the two referenced methods as discussed in Subsection 2.4.

Fig. 6. Results measured by FRI versus the ratio of overlapping nodes fp. Each datum point is obtained by averaging over 400 realizations. (a) μ = 0.1 and (b) μ = 0.3.
3.3. Real networks

In this section, several real world networks are investigated including the Zachary karate network,[28] the American college football network,[2] an electronic circuit network,[29] and a transcriptional regulation network of Escherichia coli.[29] The Zachary network has 78 links representing friendships among 34 members.[28] The network has been widely used to test the community detection methods, and is usually divided into two groups each with 16 nodes and 18 nodes. The American college football network represents the schedule of games between American college football teams in a single season, which has 115 teams and 616 competitions. The network does not have an apparent center node and is usually divided into 8–12 team communities.[4] The circuit network has 512 nodes and 819 edges in which nodes are electronic components and edges are wires.[29] In the transcriptional regulation network, nodes represent operons and an edge connecting two nodes A and B if A activates B. The transcriptional regulation network has 423 nodes and 519 edges.[29]

For making fair comparisons between the local methods, the initial starting node for the local methods is randomly selected. Each method runs 20 times on the same networks and the result is averaged. To make comparisons in the detection of disjoint communties, the SA method,[30] which has been proved to have high accuracy,[5] is also investigated. Table 1 shows the results from the SA method, the Clauset method, the Bagrow method, and our method, respectively. We also calculate the corresponding global modularity Q.

Table 1.

Results of the detection of the disjoint communities in the real networks. The values of the number of disjoint communities Cn and the global modularity Q are presented.

.

As Table 1 shows, more communities are found by our local method than by the SA method for the Football and E. Coli networks. Although the corresponding global modularity Q[4] of our local method is smaller than that of the SA, our method can detect small communities. In general, using the global methods enables us to obtain a large value of Q since the global methods are directly based on optimizing Q.[4] However, modularity has an implicit resolution limit[20] that the maximizing of modularity usually fails to obtain the groups with small sizes.[20] The results shown in Table 1 indicate that local optimization mechanisms to make communities strong enable our local method to partly solve the intrinsic resolution problem of global modularity. Next, we compare our method with several recently developed overlapping community detection methods. They are Fuzzyclust,[27] NMF,[17] and FCM.[15] The results shown in Table 2 indicate that our method performs as well as other methods.

Table 2.

Results of the detection of the overlapping communities in the real networks. On is the number of overlapping nodes, and the corresponding value of the modularity Q is also given.

.
4. Conclusions

Local community detection methods have the advantages of low computation cost and not needing to know the whole network topologies in advance. In this paper, according to the idea of “p-strong” community, we propose a local method for detecting the disjoint communities and overlapping communities. In the method, a refined agglomeration rule is designed for agglomerating nodes into local communities accurately, and the overlapping nodes are detected based on the idea of making each community strong. A coefficient is proposed to measure the contribution of node v to the community Ci, and the overlapping nodes with belonging coefficients are obtained by normalizing the to all its belonging communities. The computation cost of our local method is analyzed and is lower than those of many existing methods. We apply our method to the computer-generated networks and real networks. The simulation results show that our method performs in detecting the disjoint community better than the Clauset[8] method and the Bagrow[9] method. Moreover, our method can quickly find the overlapping nodes with belonging coefficients. The results on real networks also show that our local method is a potential way of partly solving the intrinsic resolution problem of modularity.

Reference
1Lancichinetti AFortunato SKertész J 2009 New J. Phys. 11 033015
2Davis B GCarley M K 2008 Social Networks 30 201
3Guimera RAmaral L AN 2005 Nature 433 895
4Newman M E JGirvan M 2004 Phys. Rev. 69 026113
5Fortunato S 2010 Phys. Rep. 486 75
6Danon LGuilera A DDuch J 2005 J. Stat. Mech. P09008
7Gan L Y NWu Z YGong X L 2015 Chin. Phys. 24 040503
8Chen J RHong Z MWang L NWu L 2014 Chin. Phys. 23 0118903
9Clauset A 2005 Phys. Rev. 72 026132
10Bagrow J P 2008 J. Stat. Mech. P05001
11Radicchi FCastellano CCecconi FLoreto VParisi D 2004 Proc. Natl. Acad. Sci. USA 101 2658
12Palla GDerenyi IFarkas IVicsek T 2005 Nature 435 814
13Bagrow J PBollt E M 2005 Phys. Rev. 72 046108
14Gregory S 2011 J. Stat. Mech. P02017
15Zhang S HWang R SZhang X S 2007 Physica 374 483
16Wang W JLiu DLiu XPan L 2013 Physica 392 6578
17Psorakis IRoberts SEbden MSheldon B 2011 Phys. Rev. 83 066114
18Sun P GGao LHan S 2011 Inform. Sci. 181 1060
19Sun P G 2015 Physica 419 408
20Lancichinetti AFortunato S 2009 Phys. Rev. 80 016118
21Fortunato SBarthelemy M 2007 Proc. Natl. Acad. Sci. USA 104 36
22Lancichinetti AFortunato SRadicchi F 2008 Phys. Rev. 78 046110
23Liang Z WLi J PYang FAthina P 2014 Chin. Phys. 23 098902
24Sun H LHuang J BTian Y QLiu H L 2015 Chin. Phys. 24 018703
25Shen Y 2014 Physica 393 560
26Chang Z CChen H CLiu YYu H THuang R Y2015Acta Phys. Sin.640218901(in Chinese)
27Nepusz TPetroczi ANegyessy LBazso F 2008 Phys. Rev. 77 016107
28Zachary W W 1977 J. Anthropol. Res. 33 452
29http://www.weizmann.ac.il/mcb/UriAlon/
30Guimerà RMarta S PLuís AAmaral N 2004 Phys. Rev. 70 025101