† Corresponding author. E-mail:
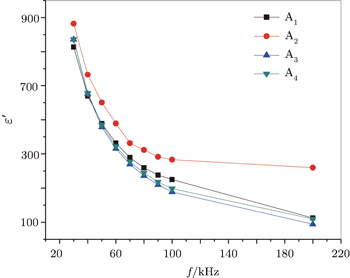
The effects of TiO2 on sintering and nonlinear electrical properties of (98.5 − x)ZnO–0.5MnO2–0.5Co,2O3−0.5Bi2O3–xTiO2 (x = 0.3, 0.5, 0.7, 0.9 mol%) ceramic varistors prepared by the ceramic technique are investigated in this work. The optimum sintering temperature of the prepared samples is deduced by determining the firing shrinkage and water absorption percentages. The optimum sintering temperature is found to be 1200 °C, at which each of the samples shows a maximum firing shrinkage and minimum water absorption. Also minimum water absorption appears in a sample of x = 0.9 mol%. Higher sintering temperature and longer sintering time give rise to a reduction in bulk density due to the increased amount of porosity between the large grains of ZnO resulting from the rapid grain growth induced by the liquid phase sintering. The crystal size of ZnO decreases with increasing TiO2 doping. The addition of TiO2 improves the nonlinear coefficient and attains its maximum value at x = 0.7 mol% of TiO2, further addition negatively affects it. A decrease in capacitance consequently in the dielectric constant is recorded with increasing the frequency in a range of 30 kHz–200 kHz. The temperature and composition dependences of the dielectric constant and AC conductivity are also studied. The increase of temperature raises the dielectric constant because it increases ionic response to the field at any particular frequency.
Zinc oxide (ZnO) ceramics with certain additives exhibit strong non-Ohmic conductions and, therefore, these materials are used for fabricating varistors-transient voltage suppression devices.[1–3] ZnO-based varistor ceramics are obtained by adding a small quantity of oxides of Bi, Sb, Ti, Co, Mn, Ni, Cr, Al, and others into ZnO powder, and then sinters it in air at the temperature ranging from 1100 °C to 1300 °C, typically at 1200 °C. The current-voltage nonlinearity of the varistor is a grain-boundary phenomenon with an ideal breakdown voltage of the grain boundary being about 3.2 V.[4–8] The majority of commercial ZnO varistors necessarily contain Bi2O3 as varistor-forming oxides and they exhibit excellent varistor properties. However, they have a few drawbacks due to the high volatility and reactivity of Bi2O3 melted at about 825 °C during a sintering above 1000 °C.[9] The former changes the varistor characteristics with the variation of the inter-composition ratio of additives, the latter destroys the multi-layer structure of chip varistors and it generates many secondary phases in addition to insulating the spinel phase deteriorating surge-absorption capabilities. The Bi2O3 is an essential additive of the ZnO varistor. Because Bi2O3 has a melting point that is far lower than those of ZnO and other additives, it exists in liquid phase in a relatively low temperature, which promotes other oxides to be distributed evenly in the ZnO grains and grain boundary.[10,11] The nonlinear current–voltage (I–V) behavior of ZnO varistors is derived from the addition of a small quantity of other metal oxides,[12] such as Bi2O3, Sb2O3, and Co3O4 since a dopant is responsible for the formation of varistor behavior.[13] It is believed that for the application of the ZnO varistors, the dopant plays an important role in modifying the defect concentration at the ZnO grain and/or of grain boundary where the performance of ZnO is sensitive to the presence of some additives even when their quantities are very low.[14] Pure ZnO is a nonstoichiometric n-type semiconductor with a linear V–I behavior. To make it nonlinear, various additive oxides are incorporated into the ZnO. Moreover, the incorporation of these oxides causes atomic defects to form in the grain and at the grain boundary, with donor or donor-like defects dominating in the depletion layer and acceptor and acceptor-like defects dominating at the grain - boundary. From a study of the defect equilibria in ZnO, Einzinger[15] has demonstrated that a defect-induced potential barrier can be formed from the unequal migration of defects toward the grain boundary. TiO2 is commonly used as a grain growth enhancing additive in ZnOBi2O3-based varistor ceramic.[16,17] This effect is attributed to the increased reactivity of the Bi2O3-rich liquid phase by introducing the titanium ions that are rapidly distributed into the liquid phase and increase the chemical activity of ZnO particles and thus accelerate their growth.[18–20] The microstructure and electrical properties of zinc oxide varistor ceramic can be modified by adding various metal oxides. As is well known the co-addition of praseodymium and cobalt into pure zinc oxide essentially induces nonlinear properties from Ohmic properties, in the voltage–current relation.[6–10] The adding of various rare earth oxides can noticeably increase the breakdown field, and improve the nonlinear coefficient.[21–30] The sintering temperature has a prominent effect on the electrical properties of ZnO varistor. According to the SEM and XRD analysis, if the temperature is too high, many of the Bi atoms will volatilize, and thus bring about many air pores in the ZnO varistor to deteriorate the structural uniformity, thereby affecting its electrical properties.[31,32]
The aim of the present work is to investigate the effects of TiO2 doping on the sintering temperature nonlinear electrical and dielectric properties of ZnO–MnO2–Co2O3–Bi2O3-based ceramic varistors.
The powders were obtained by the conventional oxide mixing method through using the following compounds ZnO(Sigma-Aldrich)–MnO2–Co2O3 (vetec), Bi2O3(Sigma-Aldrich), and TiO2 (Merck). The samples were prepared using a conventional ceramic technique with a nominal composition of (98.5 − x)ZnO–0.5MnO2–0.5Co2O3–0.5Bi2O3−xTiO2 (x = 0.3, 0.5, 0.7, 0.9 mol TiO2) and named A1, A2, A3, and A4 respectively. The raw material powders of analytical grade were mixed and ball-milled in water for 4 h with high-resistant ZrO2 balls as the medium. The resulting slurries were dried in air at 200 °C for at least 24 h, and then calcined in air at 750 °C for 2 h. The calcined mixtures were crashed into powders, sieved, and pressed into discs of 1.2 cm in diameter and 0.3 cm in thickness. These discs were processed by a semi-dry press method under 70KN. Then, the discs were sintered at 900 °C–1200 °C for 2 h. The optimum sintering temperature for all the samples was deduced from the determination of the following parameters: firing shrinkage and water absorption percentages. The method given is based on the ASTM standard (C71, C72). The structures of the prepared samples were identified using XRD on a Brucker axis D8 diffractometer of Cu-Kα radiation (λ = 1.5418 Å). Mean grain size was determined by analyzing the SEM micrographs (Joel-JEM. T200). To perform the electrical measurements, silver contacts were deposited on the sample surfaces. The I–V measurements of these samples were made by using a DC power supply in a current range up to 2 mA. The non-linearity index α) was calculated from the following equation:
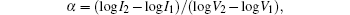
A PM 6304 programmable automatic RCL meter was used for accurately measuring the resistance, capacitance and inductance. From the measured values of the capacitance, the dielectric constants at all frequencies ranging from 30 kHz to 200 kHz were calculated at a constant temperature. The relative permittivity (ε′) and conductivity σ were calculated from the following relations: ε′ = Cd/ε0A, where C is the capacitance in unit F, d is the thickness of specimen in unit m, ε0 = 8.85 × 10−12 F/m, and A is the area of specimen in unit m2. Also from the values of resistance R, conductivity σ was calculated from the following relation: σ = d/RA.
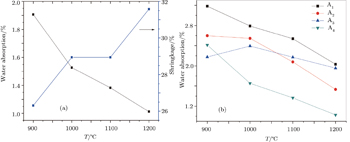
Results of physical properties indicate that better densification takes place in discs fired at 1200 °C for 2 h above which they start to deform. Low water absorption values are achieved for all mixes. Therefore, this temperature is selected as the proper maturing temperature for them. Water absorptions of different mixes decrease with increasing firing temperature and mol% of TiO2, i.e., addition of TiO2 in present Co2O3, MnO2, and Bi2O3 leads to better densification by minimizing the presence of closed pores. Minimum water absorption appears in sample (A4) of x = 0.9 mol% which equals 1.02, fired at 1200 °C for 2 h. It is evident that better densifications and minimum water absorptions are achieved in all mixes fired at 1200 °C for 2 h as shown in Fig.
Figure
Higher sintering temperature (above 1200 °C) for 2 h gives rise to the reduction of bulk density. A few pieces of sample A4 are prepared at different sintering temperatures in a range of 900 °C–1300 °C and the bulk density of the prepared sample is calculated using Archimedes’ principle (buoyancy method) and was plotted against the sintering temperature in Fig.
The results show that the composition exhibits an increase in bulk density at up to 1200 °C after which it starts to decrease. The increase in density is due to increased consolidation with temperature. Densification takes place above 1200 °C. The reduction in bulk density is due to the increase in the amount of porosity between the large grains of ZnO resulting from the rapid grain growth induced by the liquid phase sintering. Similar results were obtained by many authors.[33–35]
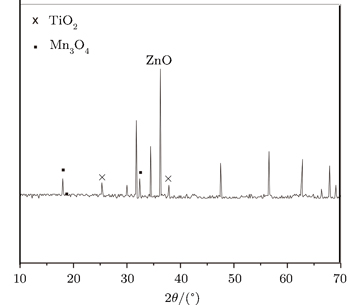
The Bi2O3 has a melting point that is far lower than those of ZnO and other additives, and thus exists in liquid phase at a relatively low temperature, which causes other oxides to be distributed evenly in the ZnO grains and grain boundary. The x-ray diffraction (XRD) result of the prepared sample A4 shows that the main crystal phases are ZnO (JCPDS-36-1451), TiO2 (JCPDS-84-1286), and Mn3O4 can be (JCPDS-01-4837) as shown in Fig.
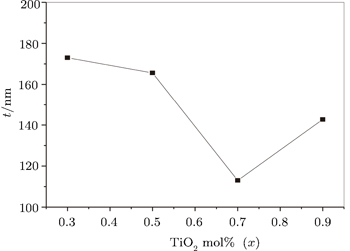
The decreasing in the crystalline size is attributed to the presence of some TiO2 and Mn3O4 at the grain boundaries which hinder the grain growth and produce an external pressure on the grains and consequently the crystallite size decreases. The microstructure of TiO2-based ZnO varistor ceramic doped with TiO2 less than 0.9 mol% mainly consists of two phases: grey bulk phase and white continuous intergranular layer (second phase). The phase composition is further confirmed by EDS. The results reveal that the grey bulk phase is a Zn-rich phase, and the white continuous intergranular layer is a Ti-rich phase as shown in Fig.

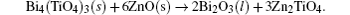
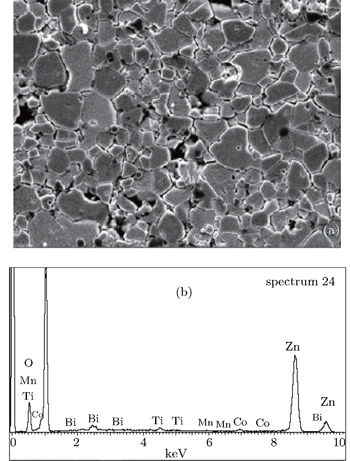 | Fig. 5. (a) The SEM image of sample A3, (b) the EDAX of the above image showing the distribution of Bi2O3, TiO2, MnO2 with ZnO and Co3O4 intergranular accumulation. |
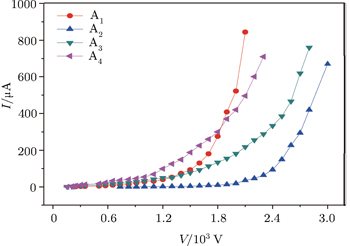
The (I–V) characteristics are measured at voltages between 0 kV and 5 kV and currents between 0 mA and 1 mA. The relations between I and V for the different mixes are shown in Fig.
| Table 1. Calculated values of the nonlinear exponent (α), breakdown voltage (Vb) of the prepared samples. . |
The results of dielectric constant as a function of frequency at room temperature of different mixes are plotted in Fig.
 | Fig. 8. The variations of AC conductivity with frequency at room temperature of the prepared samples. |
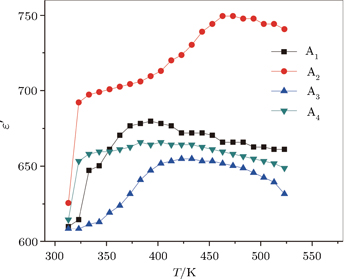 | Fig. 9. The temperature dependences of the dielectric constant of the prepared samples at frequency 30 kHz. |
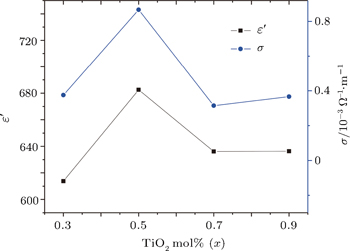
The composition dependences of the dielectric constant and AC conductivity are shown in Fig.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 |