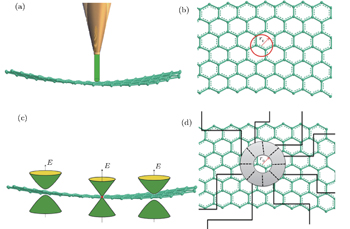
† Corresponding author. E-mail:
In graphene, conductance electrons behave as massless relativistic particles and obey an analogue of the Dirac equation in two dimensions with a chiral nature. For this reason, the bounding of electrons in graphene in the form of geometries of quantum dots is impossible. In gapless graphene, due to its unique electronic band structure, there is a minimal conductivity at Dirac points, that is, in the limit of zero doping. This creates a problem for using such a highly motivated new material in electronic devices. One of the ways to overcome this problem is the creation of a band gap in the graphene band structure, which is made by inversion symmetry breaking (symmetry of sublattices). We investigate the confined states of the massless Dirac fermions in an impured graphene by the short-range perturbations for “local chemical potential” and “local gap”. The calculated energy spectrum exhibits quite different features with and without the perturbations. A characteristic equation for bound states (BSs) has been obtained. It is surprisingly found that the relation between the radial functions of sublattices wave functions, i.e., 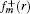

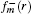

Due to the chiral nature of graphene carriers and the Klein tunneling,[1,2] quantum tunneling in these materials becomes highly anisotropic, qualitatively different from the case of normal, nonrelativistic electrons and gapless graphene cannot confine electrons via a lateral electrostatic potential.[1,3] Several setups have been found to tackle this problem, like confining Dirac electrons in rings with edge reconstruction,[4–6] also producing nanostructures of graphene in the form of quantum dots[7,8] or nanoribbons.[9,10] Confining Dirac electrons also with inhomogeneous constant magnetic fields,[11–13] superlattices over different substrates[14–16] with a modulated Fermi velocity[17] or scalar potential[18] as well as nanohole patterning[19] and topological mass terms[20–23] have been discussed. Since the successful preparation of monolayer graphene films,[24] they have stimulated a great deal of research and exhibited many unusual properties.[25–28] Among these striking properties, the relativistic-like behavior and the zero effective mass result from the unique band structure of graphene, i.e., the gapless and approximately linear energy dispersion relation near the Fermi energy at the vicinity of the K and K′ valleys in the Brillouin zone. In this paper, we study yet another alternative to confine electrons in graphene consisting in a position-dependent gap. In particular, we will study the bound-state spectrum of a created circular dot as a function of its radius. Some theoretical attempts have been suggested to trap Dirac electrons in a graphene quantum dot (GQD) and to form quasibound states by using electrostatic potentials.[29–31] Recently, other alternative approaches have been proposed by means of inhomogeneous magnetic fields.[32–35] Up to now two types of inhomogeneous magnetic fields have been used to create the graphene quantum dot (GQD). One is that the magnetic field is zero inside a circular region and nonzero outside it.[33] The other is that the magnetic field is nonzero only in a circle and zero elsewhere.[35]
As we know, it is a curious and complex situation to solve the Dirac equation with the δ potential in comparison with the equivalent problem in nonrelativistic quantum mechanics, i.e., the Schrödinger equation, which is discussed in any course on quantum mechanics. This is basically related to the fact that being the Dirac equation of first order, a singular potential, like the δ one, induces discontinuities at the level of the wave function themselves instead of the usual discontinuities that appear in the first derivative in the Schrödinger equation. The Dirac equation is a fundamental base of the relativistic field theory. However, it is an important model in the nonrelativistic solid state theory as well. Superconductors with d-pairing,[36] the Cohen–Blount two-band model of narrow-gap semiconductors,[37,38] electronic spectrum of the carbon tubes form an incomplete list of the nonrelativistic applications of this equation. During the last two years a huge ammount of attention has been spent on the problem of the electronic spectrum of graphene (see the review article.[39]). The two-dimensional structure of it and the presence of the cone points in the electronic spectrum make a comprehensive study of the external fields effect on the spectrum and other characteristics of the electronic states described by the Dirac equation in the (2+1)-dimensional space-time.
In this work, we address the BSs of the (2+1)-dimensional Dirac equation due to the short-range perturbations. The pristine graphene is gapless, but violation of symmetry between the sublattices can induce an opening of the gap.[40] The symmetry violation can be triggered by the substrate or be developed dynamically. Notice that “short-range” stands here for the lack of a long-range tail of the potential. At the same time the perturbation radius remains finite that is equivalent to the large quasi momentum cut-off.[38] This cut-off makes the quasi-momentum space form factors of the perturbation small enough for the quasi-momentum transfer of the order of the reciprocal lattice vector and, therefore, mixing of K and K′ states can be done non-effectively (this mixing was studied in Refs. [41] and [42]). Particular attention to this case stems from the effectiveness of short-range scatters in contrast to the long-range ones: an effect of the latter is suppressed by the Klein paradox.[43]
In this paper, we have investigated the perturbed Dirac equation with the local mass and local chemical potential that is a confining potential for electrons (the induced potential due to the ring segment around the circular region) perturbations. We have exploited the scattering approach to calculate the BSs energies. This paper is organized as follows. In Section 2, we present the perturbed Dirac equation in a (2+1)-dimensional space-time model; in Section 3, we present the analyses of our results; finally, in Section 4, a summary of this paper is presented.
At low energies, when the continuum limit and the effective mass approximation apply, the physics of graphene is described by two copies of massless Dirac-like Hamiltonians, which hold for momenta around the Dirac points K and K′ at the corners of the graphene’s (hexagonal) first Brillouin zone where the completely filled π-electron valence and empty π*-electron conduction bands touch.[44] The Hamiltonian and Dirac equations describing electronic states in graphene reads[39]
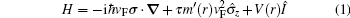
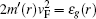
By solving the gapless Dirac equation inside the circular region with r0 radius as well as the solving of the gapped Dirac equation outside one, the spectrum energy of BSs will be obtained. The spinor structure takes into account the two-band nature. 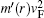
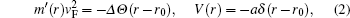
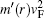
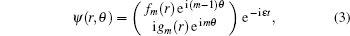
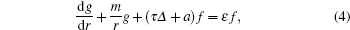
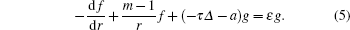
These equations have a symmetry:
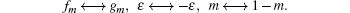
Let us introduce the function φm(r) = fm(r)/gm(r). By integrating in the vicinity of r = r0, we obtain the matching condition



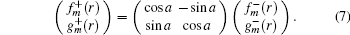
We note that the coefficients matrix is unitary and orthogonal, i.e., det (coefficients matrix) = 1 and contains the information for finding the eigenvalue equation for the BSs. On the other hand, we see that the matrix can construct the SO(2) group, that is to say, the relation between the radial 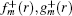
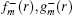
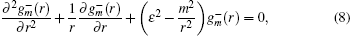
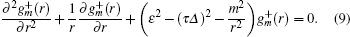
These equations are related to the Bessel equations. Their general solutions give
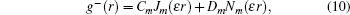


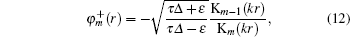
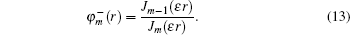
Applying the matching condition (
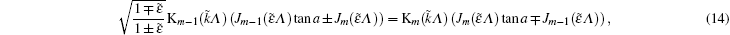
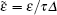
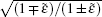
In this section, we present the most important results of BSs of electrons. We have obtained BSs of electrons of the graphene lattice in a circular region. We have applied the tight-binding Hamiltonian model plus local perturbations to describe the dynamics of electrons on one layer graphene lattice structure. We have found the BSs of electrons in the perturbated Dirac model by means of a scattering approach which gives the energy of bound states by solving a characteristic equation. Also the calculation is performed within Dirac cone approximation.
The analytical solution of the characteristic equation (
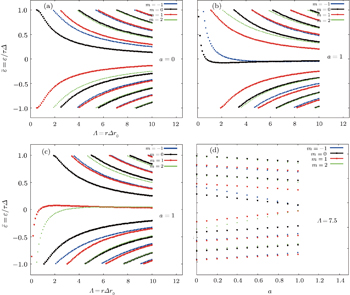
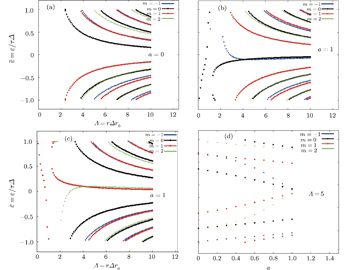
In Fig. 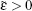

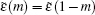
In Fig.
In conclusion, we obtained the bound electron states for the two-dimensional Dirac equation with the short range perturbations. The short-range perturbations are approximated by the step and delta function δ (r − r0) with different strengths for electrons and holes. We found the characteristic equation for the discrete energy levels. The dependence of the energy levels on the perturbation strengths was investigated both analytically and numerically. It is necessary to mention that the creation of the BSs of electrons in graphene is important in the fabrication of graphene quantum dots. Our findings show that the BSs of electrons are created with a special potential and the forms of the BSs depend on the size and sign of the potential and circular region radius. Due to the finite potential gap, asymmetry in different valleys is seen. Notice that the bound states energy levels obtained in the case of the vanishing parameter Δ are in the qualitative correspondence to the energy levels deduced from the scattering amplitude poles calculated in Ref. [48].
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 |