† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61201030, 61372045, 61472045, and 61401229), the Science and Technology Project of Jiangsu Province, China (Grant No. BE2015002), the Open Research Program of the State Key Laboratory of Millimeter Waves, China (Grant Nos. K201616 and K201622), and the Nanjing University of Posts and Telecommunications Scientific Foundation, China (Grant No. NY214148).
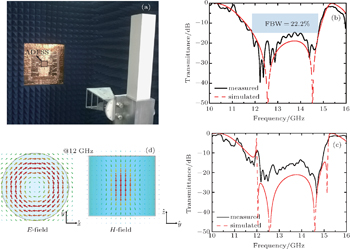
In this work, we propose an all-dielectric frequency selective surface (FSS) composed of periodically placed high-permittivity dielectric resonators and a three-dimensional (3D) printed supporter. Mie resonances in the dielectric resonators offer strong electric and magnetic dipoles, quadrupoles, and higher order terms. The re-radiated electric and magnetic fields by these multipoles interact with the incident fields, which leads to total reflection or total transmission in some special frequency bands. The measured results of the fabricated FSS demonstrate a stopband fractional bandwidth (FBW) of 22.2%, which is consistent with the simulated result.
Frequency selective surfaces (FSSs) are planar structures composed of a periodic array of unit cells that filter electromagnetic (EM) waves impinging on the surfaces.[1] They have been widely used in stealth technology, electromagnetic countermeasure, and communication systems.[1,2] Typical FSSs are composed of metallic grids or dipole arrays, which exploit the strong interactions between EM waves and metals. However, metals are problematic at very high incident power. For example, strong currents in the conductors will incur severe heating due to ohmic losses; arcing will occur at field concentration points.[3] Besides, metal materials are not quite favorable for high-temperature resistance and corrosion-resistant requirements. In Ref. [4], Li and Behdad cleverly reduced the amplitude of the local electric field by miniaturizing the metal FSS element and alternating layers of dielectric and metal grids to separate the capacitive and inductive layers. However, consider that dielectrics exhibit a much weaker interaction with the field than metals do, then all-dielectric FSSs will turn more alternative.
Recently, Barton et al.[5] developed an all-dielectric FSS (ADFSS) based on guided-mode resonance (GMR), which extends the fractional bandwidth of conventional GMR devices from 1% to 16%, and could survive with no damage at a high pulsed microwave power of 1.7 GW/m2. Barton et al.[6] designed another novel ADFSS by using genetic algorithms and fast Fourier transforms to generate random geometries, which exhibits a larger fractional bandwidth. Each of the two designs has a total height about λ0/3(λ0 is the center wavelength of the operating EM wave). In the optical region, subwavelength dielectric granules that possess strong Mie resonances are often used to fabricate double-negative metamaterials,[7] single-negative metasurfaces,[8,9] and impedance matched zero-index metamaterials.[10] Recently, a single-negative all-dielectric metamaterial, which is comprised of a single layer of cylindrical silicon resonators on a silicon-on-insulator substrate, has been experimentally proved to possess broadband perfect reflection in the infrared region.[8]
In this work, we exploit the method of all-dielectric metamaterials to develop all-dielectric FSSs, where high-permittivity dielectric resonators (DRs) are periodically placed in a three-dimensional (3D) printed supporter. The fabricated ADFSS exhibits a stop-band fractional bandwidth of 22.2% with a total height of less than λ0/6. Owing to the thinner thickness, the field of view (FOV) is also greatly improved. The symmetric structure of the device makes it insensitive to polarization.
According to Mie scattering theory,[11,12] when a plane wave impinges on a single electrically-small dielectric particle (with the relative permittivity εr = n2) located in a background material with dielectric constant εb and permeability μb, the field distribution of the scattered wave can be decomposed into multipolar components with plane wave expansions. The scattered field
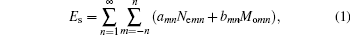
As is well known, high-permittivity dielectric cylinders can be regarded as magnetic-wall structures approximately. When EM waves enter into a DR, they will be reflected between the interfaces of the dielectric and free space continuously, which results in many resonant modes, including transverse electric (TE) modes, transverse magnetic (TM) modes, and hybrid electromagnetic (HEM) modes. For such a cavity, wave functions which are TE and TM with respect to the z direction can be written as[16]
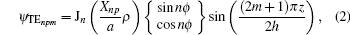

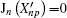
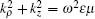

The total far field scattered by a subwavelength DR can be decomposed into multipolar components, such as dipoles, quadrupoles, and so on. In most cases, higher-order terms are negligible. Then, the reradiate EM fields by these low-order multipoles interact with the applied field and lead to the overall frequency response.
In the work presented here, high-permittivity dielectric cylinders are used as the resonators due to their amenabilities to top-down fabrication techniques. For cylinder resonators, the position of the electric or magnetic dipole mode is a function of the aspect ratio h/D, where h and D are the height and diameter of the cylinder, respectively. It has been proved that the spectral separation of the electric and magnetic resonant modes approaches to the largest spacing as h/D ∼ 1.0, which is necessary for the design of broadband reflector.[8]
Figure
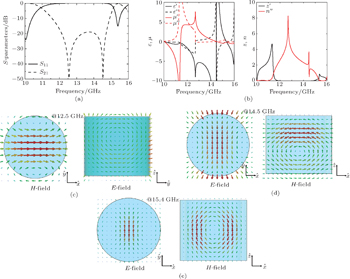
Firstly, we perform full-wave simulation with Computer Simulation Technology (CST) Microwave Studio,[17] where normally incident plane waves are assumed. Figure
In order to further explore the physical mechanism of the resonance, we obtain the time snapshots of the steady-state electric and magnetic field at the two transmission zeros and the transmission pole from the CST Microwave Studio. Figure
Then, the manufactured ADFSS is experimentally tested in our anechoic facility (shown in Fig.
For high-power incident microwaves, FSSs composed of metallic unit cells are problematic. In this paper, we present a subwavelength-thick all-dielectric FSS composed of high-permittivity dielectric resonators and 3D printed supporter, which avoids all use of metals. Incident waves enter into the DRs and lead to electric and magnetic resonances, which can be decomposed into multipolar components. The reradiated fields by these multipoles interact with the applied field, leading to the overall frequency response. This fabricated all-dielectric FSS provides 15 dB of suppression over a 22.2% fractional bandwidth and large field of view except a very narrow frequency band at 12 GHz. This method will find a variety of potential applications in high-power microwave systems including radomes, electromagnetic protections, and more.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 |