The ThCr₂Si₂-type compounds have attracted a tremendous amount of attention since the discovery of iron-based superconductors in 2008.^[1,2] Besides iron pnictides, many other 122 systems have also been extensively studied. Superconductivity was found in CaPd₂As₂ (Tc ∼ 1.27 K) and SrPd₂As₂ (T_c∼ 0.92 K) single crystals.^[3] A checkerboard antiferromagnetic (AF) structure was observed in insulating BaMn₂As₂ and relevant compounds.^[4,5] Itinerant antiferromagnetism was reported in BaCr₂As₂.^[6,7]

Cobalt-based 122 compounds are closely similar to 122 iron pnictides in many aspects. However, no superconductivity was measured in the doped SrCo₂As₂.^[8] However, a clear negative thermal expansion was observed in the compound.^[9] CaCo₂As₂ has received particular interest among the cobalt-based 122 compounds. It has a typical ThCr₂As₂ structure (space group I4/mmm) and a small ratio of c/a ∼ 2.59 under ambient pressure, suggesting a collapsed phase,^[10,11] just as was found in CaFe₂As₂. A range of external pressures can reduce its c axis by a factor of ∼ 9.5% and drive a collapsed phase transition^[12,13] with no magnetic^[12–15] or superconducting^[16] transition. Similar to the AF transition at ∼ 170 K in CaFe₂As₂, A-type AF ordering in CaCo₂As₂ was also observed by different research groups. The reported T_N ranges from 70 K to 76 K.^[17,18] It increases to 90 K with 10% Sr doping.^[17] Interestingly, a spin flop transition was observed in all the above measurements.^[17,18] However, if Sn instead of CoAs is used as flux, the crystals have a T_N of only ∼ 52 K and 7% Co vacancies.^[19,20] It is unclear if the reduction of T_N is related to Co vacancies and the issue remains an open question so far. As one of the fundamental techniques sensitive to crystal microstructures, Raman scattering has been proved to be an effective way to probe vacancies and their ordering.^[21]

Raman scattering measurements on CaCo₂As₂ were carried out in this work. At least 8 modes were observed, which is much more than the number of symmetry-allowed Raman modes. Polarized Raman measurements indicate that three of the modes have a four-fold symmetry and one has a full-symmetry. The temperature-dependent Raman spectra reveal that the strongest peak shows clear anomalies in both frequency and width near the AF transition. This is similar to the cases of 122 and 11 iron pnictides and provides the important information on vacancies in the material. The present study may provide insight into superconductivity, magnetism and collapsed phase because of the close similarity between CaCo₂As₂ and other 122 systems including the superconducting ones.

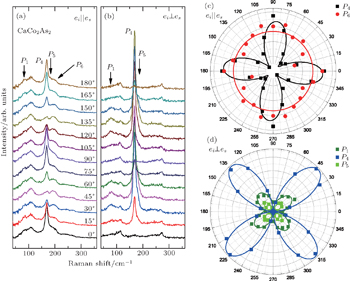
The CaCo₂As₂ crystals used in the work were grown through the self-flux method that has been described in detail elsewhere.^[13,22] Structural and thermodynamic characterizations can be found in Ref. [20]. Raman measurements were performed using a Jobin Yvon HR800 single-grating system equipped with a liquid-nitrogen cooled CCD detector and a He–Ne laser source of 632.8 nm (Melles Griot). A backscattering configuration was adopted in all the measurements. The laser power was controlled at the level of ∼ 1 mW and the laser spot was ∼ 5 μm in diameter. The cleaved surface was parallel to the ab-plane and the incident light is perpendicular to the surface or parallel to the c axis. X′X′ denotes that the polarizations of both incident and scattering light are parallel to the diagonals between a and b axes, while X′Y′ means that their polarizations are orthogonal. Polarized Raman measurements were made at room temperature by fixing the perpendicular polarizations between incident and scattering light and rotating crystal at a step of 15°. The space and point groups of CaCo₂As₂ are I4/mmm and D_4h respectively, which allows 4 Raman-active modes including one A_1g mode, one B_1g mode, and doubly degenerate E_g mode (see the inset of Fig. 1).

Figure 1 shows polarized Raman spectra at room temperature. There are 8 peaks under two configurations. Four of them appear in the parallel channel (X′X′) and the other four in the cross channel (X′Y′). On the other hand, only A_1g (As) and B_1g (Co) are symmetry-allowed under the present configuration. This means that six of the observed modes are unexpected. One may argue that the extra modes come from the intensity leakage of E modes if the crystal surface is a little tilted. However, the scenario seems incompatible with the observations since the leakage intensity is usually very small and there are only four modes totally even if all the symmetry-allowed modes are counted. Local vibrations induced by impurities also seem unlikely since no signal of impurities is seen in the structural measurements.^[18] Another possibility is that the extra modes are contributed by the local modes which are induced by Co vacancies. As mentioned above, powder x-ray diffraction and elastic neutron scattering^[19,20] indicate that ∼ 7% Co vacancies exist in the crystals with Sn as flux. Most of the observed peaks are very broadened with a full width at half maximum (FWHM) of more than 20 cm⁻¹. This coincides with the local modes, and implies that Co vacancies exist not only in the crystals grown with Sn flux but also in the crystals with CoAs as flux. It is likely that the vacancies cause a relaxation of selection rules and introduce some non-Raman active or non-Gamma modes into the Raman channel. The strong and narrow P₄ peak in Fig. 4 can be reasonably assigned to the intrinsic mode of bulk crystals.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Polarized Raman spectra collected at room temperature. The inset shows the vibration patterns of four Raman-active modes in 122 system.

We further made polarized Raman measurements by rotating crystals to resolve mode symmetries. The spectra are shown in Figs. 2(a) and 2(b). P₄ exhibits periodic modulations in intensity and P₆ remains almost unchanged in the parallel configuration, while P₆ disappears and the intensities of P₁, P₄, and P₅ change with rotating crystals. The rotation-angle dependence is illustrated in Figs. 2(c) and 2(d) respectively. Under parallel polarization configuration, the intensities of P₄ are proportional to sin 4θ, indicating a four-fold rotation symmetry, while P₁, P₄, and P₅ exhibit the four-fold symmetry in cross polarization configuration and have a phase difference of 45°. These results allow to attribute P₄ and P₆ to B_1g and A_1g modes respectively. P₅ is a B_1g-like mode which may originate from local vibrations as discussed above. The vibration patterns of B_1g and A_1g modes are exactly similar to those in BaFe₂As₂ and illustrated in the inset of Fig. 1.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Rotation-angle dependence of Raman spectra in CaCo2As2. (a) and (b) Raman spectra collected under parallel and cross polarization configurations respectively. (c) and (d) Intensity modulations with rotation angles in two configuration channels. The angles are the ones between a axis and polarization of incident light.

The temperature-dependent Raman spectra are shown in Fig. 3. All the observed modes become softening and broadening with increasing temperatures. We made careful Lorentz fitting for the strongest P₄ peaks and the fitting results are summarized in Fig. 4. The evolution of Raman frequency with temperature coincides with the inharmonic phonon decay model.^[23] This suggests that CaCo₂As₂ has a normal positive thermal expansion which is opposite to the clear negative thermal expansion observed in SrCo₂As₂.^[9] The contrast difference may stem from the absence of a collapsed phase in SrCo₂As₂.^[24] The anomalies in mode width are observed around Neel temperature T_N ∼ 74 K. In fact, the reversal of temperature evolution of mode widths starts even at ∼ 150 K, far beyond T_N. This is considered as a precursor effect of AF transition. In the parent compound BaFe₂As₂ of 122 Fe-based superconductors, phonon anomalies have been reported near spin-density-wave (SDW) transition and are attributed to phonon self-energy renormalization induced by the SDW gap opening.^[25–27] Just like BaFe₂As₂, CaCo₂As₂ is also an AF metal and its magnetic transition can similarly lead to phonon anomalies around transition temperature through some form of spin-phonon interaction.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Temperature-dependent Raman spectra of CaCo2As2.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Temperature dependence of P4 phonon’s frequencies and widths. The red line is the fitting curve using inharmonic phonon decay model.

In summary, Raman scattering studies of collapsed phase CaCo₂As₂ have been made in this work and at least 8 peaks are observed. Two of them are assigned as intrinsic A_1g and B_1g modes, and the other ones are considered to come from the local vibrations induced by Co vacancies. Polarized Raman measurements determine the four-fold symmetry of the system, which put strong constraints on the possible patterns of Co vacancies. Further temperature-dependent experiments reveal that the anomalies of B_1g mode in width are related to the AF transition through a spin-phonon coupling.