† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11474339), the National Basic Research Program of China (Grant Nos. 2010CB923000 and 2011CBA00100), and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB07020100).
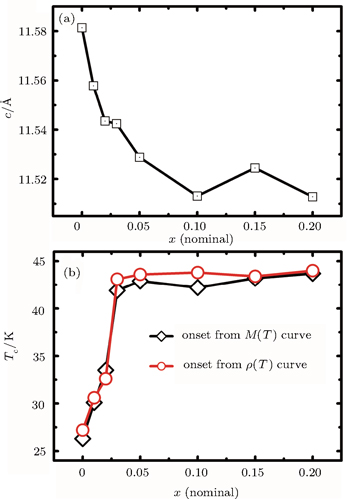
In this article, the Sm-doping single crystals Ca1 − xSmxFe2As2 (x = 0 ∼ 0.2) were prepared by the CaAs flux method, and followed by a rapid quenching treatment after the high temperature growth. The samples were characterized by structural, resistive, and magnetic measurements. The successful Sm-substitution was revealed by the reduction of the lattice parameter c, due to the smaller ionic radius of Sm3+ than Ca2+. Superconductivity was observed in all samples with onset Tc varying from 27 K to 44 K upon Sm-doping. The coexistence of a collapsed phase transition and the superconducting transition was found for the lower Sm-doping samples. Zero resistivity and substantial superconducting volume fraction only happen in higher Sm-doping crystals with the nominal x > 0.10. The doping dependences of the c-axis length and onset Tc were summarized. The high-Tc observed in these quenched crystals may be attributed to simultaneous tuning of electron carriers doping and strain effect caused by lattice reduction of Sm-substitution.
Among the iron-based high-Tc superconductors, the 122-type ternary compounds A/Fe2As2 (A = Ca, Sr, Ba, and Eu) crystallize in the tetragonal ThCr2Si2-type crystal structure at room temperature, and they undergo a spin density wave (SDW) transition around 140 K ∼ 200 K, which is also accompanied by a structural transition from tetragonal to orthorhombic phase at similar temperature.[1–5] Bulk superconductivity was achieved in these compounds by suppressing the antiferromagnetic SDW ordering via hole or electron doping, even external pressure, etc., and their superconducting Tc is usually below 38 K.[6–11]
While interestingly, unexpected high-Tc above 40 K was realized in some rare-earth-doped Ca1 − xRxFe2As2 compounds (R = La, Ce, Pr, and Nd), with the highest Tc up to 49 K in Pr-doped CaFe2As2.[12–16] This higher Tc phase in electron doped CaFe2As2 is usually filament type with poor superconducting behaviors and highly anisotropic characteristics.[12,13,15,17,18] Some possible reasons were proposed to explain the occurrence of this higher Tc phase, such as crystallographic strain, doping inhomogeneity, and crystal defects, etc.[13,19–23] On the other hand, CaFe2As2 is actually special in these 122 compounds, it has the shortest c-axis parameter and the smallest cell volume, which places it near the critical point for a unique collapsed structural phase transition.[9,12,24–32] Generally, the pristine tetragonal CaFe2As2 enters into the orthorhombic SDW phase around 170 K, while under a mild external pressure of 0.35 GPa, a collapsed, non-magnetic tetragonal phase would be formed at lower temperature without the formation of SDW phase.[24,25] This collapsed phase can also be stabilized by chemical substitution or furnace quenching processes.[9,12,26–30] Moreover, La and P co-doping in CaFe2As2 enhances both the superconducting transition temperature and the shielding volume fraction, which is suggested to be from the simultaneous tuning of the reduction in cell volume and the electron carrier doping.[33] Similar results occur in the La and Ru co-doped CaFe2As2 single crystals.[27] Due to the smaller ionic radius of Sm3+ than Ca2+, the substitution of Sm3+ for Ca2+ may be a suitable method for the structure and carrier modulation in CaFe2As2. While the doping of Sm3+ for Ca2+ is experimentally difficult due to structural instability, and previous study found no clear superconductivity in slightly Sm-doping CaFe2As2 single crystals grown from FeAs flux.[34]
In this article, we report the successful growth of the Sm-doped CaFe2As2 single crystals from CaAs flux. Superconductivity with Tc varying from 27 K to 44 K was observed in these crystals, with a relatively substantial shielding volume fraction obtained in the nominal Ca0.8Sm0.2Fe2As2 single crystal.
Single crystals of Ca1 − xSmxFe2As2, with x = 0, 0.01, 0.02, 0.03, 0.05, 0.10, 0.15, 0.20, were grown using the CaAs flux method. A mixture of Ca, Sm, FeAs, and As with a mole ratio of Ca:Sm:FeAs:As = (3 − 3x):3x:2:2 was loaded into an alumina crucible and sealed in an evacuated quartz tube. The ampoules were placed in a muffle furnace and heated at 500 °C and 700 °C for 5 h successively, then slowly heated to 1150 °C for 10 h, maintained at 1150 °C for 30 h and then cooled down to 850 °C slowly at a rate of 1.5 °C/h, followed by quenching in ice-water rapidly. Plate-like single crystals up to 1-mm long were obtained after the flux was removed by washing the products in de-ionized water. The FeAs precursor was pre-sintered by reacting stoichiometric amounts of Fe and As inside an evacuated quartz tube at 750 °C for 30 h.
The obtained plate-like single crystals were characterized by x-ray diffraction (XRD) from 10° to 70° at room temperature, using a PAN-analytical diffractometer with Cu–Kα radiation. The resistive measurements were carried out by employing a standard four-probe method in a quantum design physical property measurement system (PPMS) down to 2 K. The DC magnetic susceptibility was measured using a quantum design magnetic property measurement system (MPMS) with both zero field cooling (ZFC) and field cooling (FC) methods at a magnetic field of 10 Oe (1 Oe = 79.5775 A/m).
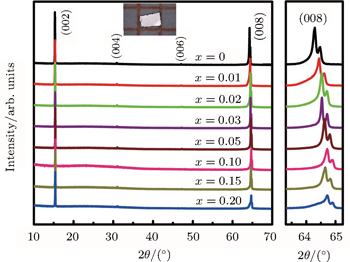
The room temperature XRD patterns for all the single crystals of Ca1 − xSmxFe2As2 samples were presented in Fig.
In Fig.
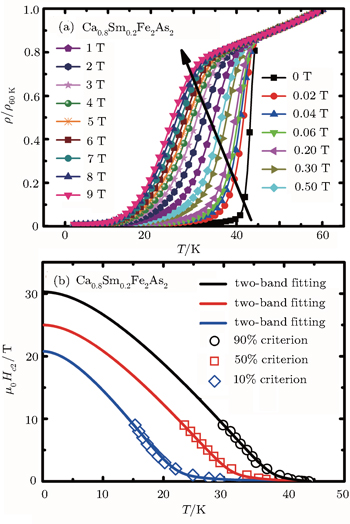
To estimate the upper critical field, the resistive superconducting transition for a Ca0.8Sm0.2Fe2As2 single crystal was characterized between 2 K and 60 K under magnetic fields of 0 T ∼ 9 T applied along the c axis, as shown in Fig.
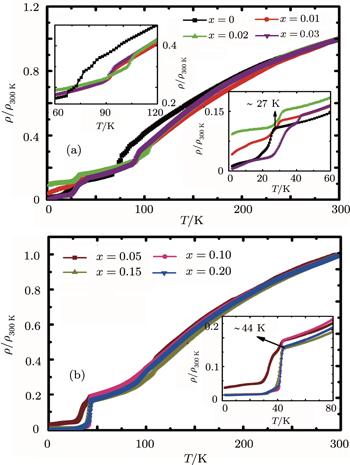
In Fig.
In Fig.
In conclusion, we successfully grew the single crystals of Ca1 − xSmxFe2As2 (x = 0.00 ∼ 0.20) using a CaAs flux method followed by a rapid quenching process. The Sm-doping was elucidated by the reduction of c-axis parameter with increasing x, and superconductivity was observed in all the Sm-doped crystals. High-Tc superconductivity up to 44 K was proved by both the resistive and magnetic measurements in the Sm-doped CaFe2As2 single crystals.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 |