Grain boundaries (GBs) are typical crystalline defects present in high temperature superconductors (HTSs). By growing a film epitaxially on a bicrystalline substrate, a bicrystal GB in the film can be formed. The misorientation and the location of bicrystal GBs can be well controlled. Bicrystal GB Josephson junctions, formed at bicrystal GBs in superconducting films, are widely used in THz wave detection or superconducting quantum interference devices (SQUIDs). The response of YBa₂Cu₃O_7−δ (YBCO) bicrystal Josephson junctions up to 4.25 THz at liquid nitrogen temperature (77 K) has been reported.^[1]

In recent years, the fundamental property of vortex motion in HTS with GBs has become a hot topic of vortex dynamics.^[2–9] The GB can be described as a collective line of artificial pinning defects, which suppresses the onset of vortex penetration and increases power dissipation. It has been demonstrated that the critical current density (J_c) across GBs in HTS decreases exponentially with the increase of misorientation angle of the GB.^[10,11] However, the complex vortex motion behavior in the GB of HTS is still not well understood. In some work, it was found that GBs can act as easy-flow channels for longitudinal vortex motion,^[12–14] because the Lorentz force (F_L) pushes vortices along the GBs when GBs are perpendicular to the current flow. In that case, J_c should decrease with increasing magnetic field. In contrast, some work shows that GBs act as barriers for vortex motion,^[15–18] since F_L pushes vortices across the GBs transversally when the GBs are parallel to current flow, resulting in the enhancement of J_c. Moreover, lots of theoretical calculations and simulations^[19–22] suggest that the vortex pinning of the GB depends on the angle between the Lorentz force and the GB orientation. In this paper, we study the dependences of J_c on the magnetic field for YBCO bicrystal Josephson junctions with the GB inclined to the current direction at different angles. We also measure the longitudinal (along current direction) and transversal (vertical to current direction) I–V characteristics of the YBCO film bridge with a GB at an inclined angle of 30° to study the vortex motion properties at the GB.

The YBCO films each with a thickness of 100 nm and a J_c of 3.9 MA/cm² were deposited on MgO bicrystal substrates (c-axis (001) orientation) using the physical vapor deposition method. The bicrystal substrates were formed by hot pressing two single crystals ((001) orientation) each with a tilt angle of 24°. The following epitaxial growths of YBCO films on these substrates result in the formation of GBs in films each with a misorientation angle (θ_c) of 24°. The measured superconducting transition temperature (T_c) of YBCO film without a magnetic field is 87 K. Then, three 10-μm-wide bicrystal microbridges are patterned on the same bicrystal film (10 mm × 10 mm) by photolithography and ion beam milling. Here, the GB orientations were inclined to the current direction with angles (θ) of 90°, 60°, and 30° (see Fig. 1), respectively. For comparison, a microbridge of YBCO film onto MgO single-crystal substrate, i.e., no GB existed, was also fabricated. The geometry of this single-crystal microbridge was the same as those of the other three bicrystal microbridges.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. YBCO microbridges with a GB inclined to the current direction at θ = 90° (a), 60° (b), and 30° (c), respectively. (d) A microbridge of YBCO film without GB. The length and width of four microbridges are all 30 μm and 10 μm.

The samples were characterized using a physical property measurement system (PPMS-9). They were located in an adjustable DC mangnet with the direction of magnetic field (H) being perpendicular to the film plane (up to 8 T).

We measure J_c values each as a function of H at 70 K for the YBCO microbridges with GBs at θ values of 90°, 60°, and 30° and without GB as illustrated in Fig. 2.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Plots of critical current density of YBCO microbridges having GBs versus H with different θ values at a temperature of 70 K (left-hand longitudinal axis). The black squares show Jc–H characteristics of microbridge without GB (right-hand longitudinal axis).

When H = 0, the J_c of YBCO microbridge without a GB is 4.2 MA/cm², while the J_c values of the other three microbridges with GBs are J_c(θ = 30°/0 T) = 45.0 kA/cm², J_c(θ = 60°/0 T) = 20.0 kA/cm², and J_c(θ = 90°/0 T) = 15.5 kA/cm², respectively.

When H ≠ 0, the J_c values of four microbridges decrease with increasing H, and J_c (no GB) > J_c(θ = 30°) > J_c(θ = 60°) > J_c(θ = 90°). As H increases from 0 T to 1 T, J_c of the microbridge with a GB decreases sharply. When H > 1 T, the reduction rate of J_c is much lower. For the three microbridges with GBs, when H is below 1 T, the DC Josephson effect dominates, leading to a high reduction rate of J_c as H increases. When H is large, the intrinsic properties of YBCO GB play an important role, thus the drop of J_c slows down, and the properties of the microbridge with GBs are similar to those of a strong correlation superconductor. With increasing H, the J_c values of the three microbridges with GBs gradually approach to each other. As H > 7 T, they are nearly the same.

The first and obvious factor contributing to the increase of J_c with the decrease of θ for the three microbridges with GBs is the increase of the GB plane area, which determines the current carrying cross section. The GBs in these three samples are all inclined to the current direction at angles of 30°, 60°, and 90°, respectively, so the corresponding GB plane areas inside bridges are 2tw, 1.15tw, and 1tw, respectively, where t denotes the thickness of film and w is the width of microbridge.

If the GB plane area is the only factor determining critical current (I_c), I_c should be proportional to the GB plane area. In Fig. 3, samples A and B denote YBCO film microbridges with GBs at θ values of 90° and 30° respectively. The widths of the two microbridges are the same. Therefore, the GB plane area of A is tw, while the GB plane area of B is 2tw. Sample C denotes the microbridge with a GB at θ = 90°. The width of microbridge of C is twice that in A, and the GB plane area of C is 2tw. If the relationship of I_c and the GB plane area is linear, the I_c values of three samples should satisfy 2I_c(A) = I_c(B) = I_c(C). Correspondingly, 2J_c(A) = J_c(B) = 2J_c(C). However, the experimental results do not obey the above relationship, and I_c(B) > I_c(C) (the data is not shown here). Based on the data in Fig. 2, we can obtain J_c(θ = 30°/0 T)/J_c(θ = 90°/0 T) = 45.0/15.5 > 2, and J_c(θ = 30°/0.2 T)/J_c(θ = 90°/0.2 T) = 17.0/6.5 > 2. These results indicate that J_c is not proportional to the GB plane area when the width of microbridge is constant. Therefore, the increase of GB plane area is not the only reason for the increase of J_c as θ reduces.

Fig. 3.

	Figure Option ViewDownloadNew Window
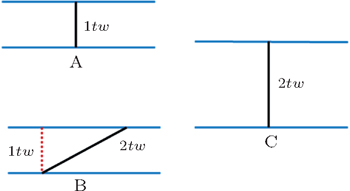	Fig. 3. Diagrams of three different microbridges with GBs at different inclined angles or having different widths. The black line denotes the GB line.

Based on the above analysis, there should be other factors influencing the J_c of a microbridge with a GB. One possible factor is the vortex motion at the GB. Lots of vortices preferentially penetrate into GBs when a magnetic field is applied due to the high energy dissipation of GBs. The GB can be described as an easy-flow channel with a strong pinning effect on vortex motion. Even at 0 T, the self-field of current can create lots of Abrikosov vortices,^[13,23] which appear at the GB first. Dissipation in current biased HTS film is caused by the vortex motion. In an HTS film microbridge with a GB, when the applied current is larger than I_c, F_L drives vortices to move along the GB, and resistance appears, i.e., the superconducting state disappears. In the GB, the vortex is affected by F_L and (the GB pinning force). The has two orthogonal components, i.e., F_GB∥ and F_GB⊥, which are schematically analyzed in Fig. 4. It is noted that is anisotropic. F_GB⊥ is large while F_GB∥ is much smaller than F_GB⊥.^[2] Despite that, the direction of total force F_∑ is parallel to the orientation of the GB. As the current increases, F_L increases. The vortices do not move until F_Lcos α > F_GB∥, where α denotes the angle between the GB and F_L, and α = 90°–θ. Once vortices start to move along the GB, the superconducting state disappears. For the three microbridges having GBs, the F_GB∥ values are the same. Therefore, F_Lcos α keeps constant when the vortices move along the GB. As α increases, or θ reduces, the critical value of the Lorentz force F_L increases, resulting in the increase of J_c.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Force analysis of a vortex in the GB. The vortex is affected by FL and , and the latter can be decomposed into FGB∥ and FGB⊥. Alphabet α denotes the angle between FL and GB.

To further investigate the vortex motion in bicrystal GBs, we measure the transverse and longitudinal I–V characteristics of the YBCO microbridge with an inclined GB, each as a function of the magnetic field at 75 K. Here, the GB is inclined to the current direction (x) at an angle of 30°. The dimensions of YBCO film microbridge are 30 μm×10 μm×0.1 μm. Six electrodes patterned by photolithography and ion beam milling are used for electrical measurement as shown in Fig. 5(d), and are two leads for longitudinal voltage (V_xx) measurement, whereas and are leads for measuring the transversal voltage, i.e., Hall voltage (V_xy). The current applied along the x direction is slowly increased (10 μA/s) for data acquisition.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. I–Vxx (a) and I–Vxy (b) characteristics of a YBCO film bridge with an inclined GB at a angle of 30° in different magnetic fields at 75 K, (c) the close-up of panel (a) at a lower current. (d) A photo of the sample.

Figures 5(a) and 5(b) show that both V_xx and V_xy linearly increase with the increase of current when the current is lower than 13 mA, which indicates that vortex motion appears only inside the GB. When the applied current is higher than 13 mA, F_L is larger, I–V_xx curves in magnetic fields above 0.5 T diverge from a linear relationship, and the transition current for diverging decreases with magnetic field increasing. Meanwhile, I–V_xy curves almost keep linear. At the transition point where the I–V_xx curve diverges from linearity, a few vortices inside the GB driven by Lorentz force break out of the GB, and mainly move along the direction of the Lorentz force (negative y-axis direction), which significantly enhances the V_xx value. However, it has little influence on V_xy. As the magnetic field increases, the vortex density increases. As a result, the driving current for the I–V_xx curve starting to diverge from linearity decreases, and the nonlinearity of the I–V_xx curve becomes more pronounced.

Figure 5(c) shows a detailed view of Fig. 5(a) at low applied current and 75 K. With increasing magnetic field, the critical driving force for the onset of the vortex motion in the GB becomes smaller. Correspondingly, I_c becomes smaller. Actually, the increase of magnetic field leads to the decrease of . Besides Josephson effects (the negative curvature of the I–V_xx curve), several step-like jumps are observed in the I–V_xx curve at 0.01 T, which is most likely due to the change of the vortex lattice in the GB. This phenomenon is often observed in a low magnetic field, and also in good agreement with the simulation results of Ref. [19].

In this work, we investigate the dependences of J_c on H for YBCO microbridge with GBs at different θ values at 70 K. The difference in J_c is mainly attributed to two reasons: (i) the different GB plane areas and (ii) the different vortex motion dynamics at the GB. Once the applied current goes beyond a critical value, the vortices pinned in the GB will move along the GB, and the superconducting state of YBCO film will disappear. We also investigate the vortex motions in a YBCO microbridge with an inclined GB at θ = 30° by characterizing its transverse and longitudinal transport property in magnetic fields. It is found that the I–V_xx curves diverge from linearity at large current and the I–V_xy curves almost keep linear, indicating that some vortices break out of the GB due to the drive of Lorentz force. Step-like jumps are observed in the I–V_xx curve at low magnetic field, which is most likely because of the change of the vortex lattice in the GB.