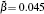A Skyrmion is a topologically stable spin texture which consists of opposite core spins and peripheral spins swirling up with a unique spin chirality determined by the underlying chiral crystal structure of the hosting material.^[1,2] Since they were observed in 2009,^[3] magnetic Skyrmion crystals (SkX) have been extensively investigated, and by now they have been discovered in various materials. There are three kinds of materials. (i) The cubic chiral B20-type helimagnets with lattices exhibiting broken or lacking parts. The materials configurations can be crucially stabilized by the strong Dzyaloshinskii–Moriya interaction (DMI) in these materials,^[4] such as MnSi,^[5–7] Fe_1−xCo_xSi,^[8,9] FeGe,^[10–12] β-Mn-type chiral magnet,^[13] and Cu₂OSeO₃.^[14,15] (ii) The non-spiral materials where the Skyrmions state can be induced by the competing of exchange interaction with other strong magnetostatic interactions^[16–18] whether there is DMI or not, i.e. the four-spin interaction, typically the monolayer Fe/Ir (111) where the 3d–5d hybridization between the Fe monolayer and the Ir substrate plays a key role in determining the unusual magnetic properties.^[16,17,19] (iii) The artificial material in which an artificial skyrmion is created by embedding a magnetic vortex into an out-of-plane aligned spin environment.^[20–22] Skyrmions are very promising for applications in spintronics^[23,24] due to their topological stabilities, ultimate small sizes and low dissipations, and varieties of methods have been proposed to control the creation, movement and removal of a Skyrmion.^[20,25,26] Proposals of manipulations and operations of Skyrmions are highly desired.^[27]

A Skyrmion can be manipulated with ultralow energy consumption due to its extremely small threshold current density (∼10⁶ A·m⁻²) compared with that of a domain wall in ferromagnet (∼ 10¹¹ A·m⁻²), because the Skyrmion lattices in a chiral magnet are coupled very weakly to the atomic crystal structure and pinned very weakly to disorder, and electric currents couple very efficiently to Skyrmions in addition.^[23] When an electric current flows through a ferromagnetic metal, the conduction electron spins are coupled ferromagnetically to, i.e., forced to be parallel to the localized spin at each atomic site by Hund’s-rule coupling, eventually collecting a Berry phase, which arises from an emergent electromagnetic field or fictitious electromagnetic field in real space. At the same time the current becomes spin-polarized, and spin angular momentum is transferred to the magnetization through the mechanism known as spin-transfer torque (STT) due to spin conservation.^[28] Consequently the electron current drives the flow of Skyrmions. The motion of the Skyrmions leads to a temporal change of the emergent magnetic field and hence to an emergent electric field due to electromagnetic induction. On the one hand, the induced emergent electric field acts on the electrons like the ordinary magnetic field, and, in particular, gives rise to a Lorentz-type force, which deflects electrons and results in the topological Hall effect.^[29–32] On the other hand, the velocity of the Skyrmion has its transverse component, that is, the Skyrmion Hall effect arises, albeit with a small constant.^[29,33,34] However, Skyrmions can also be manipulated by the magnon current induced by thermal gradient due to the coupling of magnetization to magnonic spin transfer torque even in the absence of charge flows, and move from the cold to the hot region.^[35,36] Recently, Troncoso and Núñez have shown that thermal torques can increase the mobility of Skyrmions by several orders of magnitude.^[37] The progress in the magnetic skyrmions in chiral magnetic materials has been reviewed in Refs. [38] and [39].

In the present study, we investigate the dynamics of Skyrmions in a thin film of metallic chiral magnet in the presence of a thermal gradient and an electric current. Based on the stochastic Landau–Lifshitz–Gilbert–Slonczewski (LLGS) equation^[40] the dynamic equation for Skyrmions is derived. The equation is in the form of a generalized Thiele’s equation that describes the dynamics of a single Skyrmion at finite temperature. The results show that the Hall angle can be manipulated by the spin-transfer torque induced by a magnon current and an electric current. Based on the dependence of the Hall angle on the ratio of the thermal gradient to the electric current density, a Skyrmion valve is proposed.

We consider a thin film of a metallic chiral magnet well below the Curie temperature (Fig. 1), which is described by the magnetic free energy density F(m∂_im) (here i = xy; double indices are summed over)

Fig. 1.

	Figure Option ViewDownloadNew Window
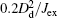
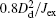
	Fig. 1. Schematic of device, where the electric current flows from left to right and the applied magnetic field is perpendicular to the thin film.

The standard Landau–Lifshitz–Gilbert (LLG) equation is phenomenological and widely used to model magnetization dynamics, including the dynamics of the magnetization direction of the skyrmion lattice due to the very smooth magnetic structure in the skyrmion lattice phase and slight changes of its amplitude. Slonczewski has studied the effect of current-driven spin-transfer torque on magnetization.^[40] However, when one studies the dynamics of skyrmions in metal magnets it is necessary to introduce another two novel damping terms relevant to non-collinear spin textures, −α′{m·[∂_im × ∂_tm]}∂_im originating from Ohmic damping of electrons coupled by Berry phases to the magnetic structure,^[24,36] and −β′{m·[∂_im × (υ_s·∇)m]}∂_im for the need of Galilean invariance, where v_s is an effective spin velocity parallel to the spin current density. These terms might actually be the dominating ones in a good metal^[46] except for non-adiabatic spin-transfer torque βm × (υ_s·∇)m.^[47] So the extended LLGS equation^[40] containing h_l the random fluctuating of H_eff is expressed as

Here, γ = M_s/s is the gyromagnetic ratio, s the saturation spin density, υ_s = −(pa³/2eM_s)j is the spin velocity of the conduction electrons defined as the ratio of the spin current to the size of the local magnetization for smooth magnetic structures with constant amplitude of the magnetization,^[46] with p being the spin polarization of the electric current density j, which is over the threshold current density, e (> 0) the elementary charge, and a the lattice constant, while α denotes the Gilbert damping coefficient. The LLGS equation contains the adiabatic spin-transfer torque given by (υ_s·∇)m, and the non-adiabatic spin-transfer torque given by β(m × v_s·∇)m, where the strength of the non-adiabatic spin-transfer torque is characterized by the parameter β. The random Langevin field h_l, which describes the fluctuating torques, is defined by the uncorrelated Gaussian white noises^[48]

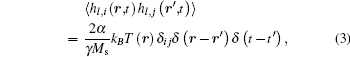
The effective field is derived from the free energy density, Eq. (1), as follows:

Induced by the magnon current, the normalized magnetization m can be decomposed into the slow component m_s corresponding to the equilibrium configuration of the Skyrmion, and the fast component m_f orthogonal to m_s:^[36]

Following the procedure in Refs. [49] and [50] and the coarse-graining over m_f where linear terms in m_f can be discarded by taking the average over time because m_f is a fast mode behaving as a function of the sine or cosine form in time,^[36] equation (2) becomes

Following the Thiele approach,^[51] a modified version of Newton’s equation describing the translational motion of a Skyrmion domain^[52] is derived by multiplying both sides of Eq. (6) with m_s × (cross product) and then with m_s· (dot product), and integrating the resulting equation over the area around the Skyrmion or the Skyrmion domain finally^[46] the following equation is obtained:

Here the first term on the left-hand side of the above equation describes the Magnus force. The gyromagnetic coupling vector G = −4πe_z with e_z being the unit vector along the z direction or the direction of the applied field. Ṙ = ∂_tR is the drift velocity of the Skyrmion. The second term represents the friction of the Skyrmion. The components D_ij of the tensor D are D_xx = D_yy = D and 0 otherwise. Similarly, the components D′_ij of the tensor D′ are D′_xx = D′_yy = D′ and 0 otherwise. The first and second term on the right-hand side are the forces on Skyrmions arising from electric current (F_c) and magnonic current or temperature gradient (F_m). The third term F_pin is the force acting on the spin texture from the boundaries, impurities, magnetic field, etc. Our attention focuses on the motion driven by the current transverse to the edge. The Skyrmions are affected by a repulsive potential from the boundary only within a range of about a size of a Skyrmion, and cannot reach the boundary because it cannot overcome the repulsive potential if the electric current density is not over 10¹¹ A/cm².^[53] So it is reasonable to neglect the effect of boundary when Skyrmions are far from the boundary. The F_pin can be neglected also when |Gv_s| ≫ |F_pin| is satisfied.^[54]

For the steady translation motion, the magnetization profile of a rigid Skyrmion domain is represented by m_s(r,t) = m_s(r − R(t)) where R(t) = υ_dt, υ_d is the drift velocity of the Skyrmion,^[36,37,54] when the electric current is flowing in the x direction while the magnon current is flowing in the y direction as shown in Fig. 1. The present situation can be described by setting v_sy = J_y = 0, F_pin = 0, v_sx = v_s and J_x = J in Eq. (7). The resulting drift velocity components perpendicular and parallel to the flow direction of the electric current read

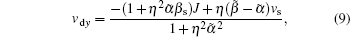
Inserting the outcome of the previous section into the definition of the Hall angle θ_H, we have

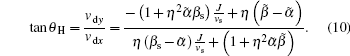
From Eq. (10), it is evident that tanθ_H → ∞ or θ_H ≈ π/2 as , and or θ_H ≈ −π/2 as J/v_s → ∞. In Fig. 2, we show the dependence of the Hall angle on the ratio of magnon current density induced by the thermal gradient to electric current density for typical parameters. So the maximal (minimal) Hall angle approaches π/2 (−π/2). Thus the Hall angle can be controlled in a wide range, which is useful in spintronics.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Dependence of the Hall angle on J/vs. For estimates we have taken , , βs = 0.032, and η = 1.4.

Finally, we propose a Skyrmion valve in confined geometries based on the control of the Hall angle. The setup of the Skyrmion valve is shown in Fig. 1. The Skyrmion can indeed be drained by an additional terminal, like the setup reported by Jiang et al.^[56] Then the Skyrmion will be driven by the Magnus force and the dissipative force, and may arrive at any of the edges of the thin film. Subsequently, the repulsive potential of the boundary induces a motion transverse to the boundary because of the Magnus force,^[53,54,57] and eventually the Skyrmions would move along the edges from left to right due to the edge effect.

Generally, , so Under these conditions the Hall angle can be reduced into

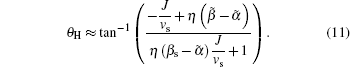
The Skyrmion would move along the A channel when θ_C < θ_H, that is,

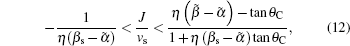
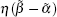
Obviously, there is an equilibrium between the transverse force induced by electric current and the longitudinal forces induced by magnon current when

When the equilibrium is reached, the value of β_s becomes

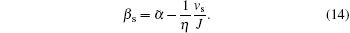
This provides a method to measure β_s with the Skyrmion valve if the parameters and η are known. Obviously, there are no Skyrmions flowing from left to right when .

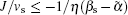
Similarly, the Skyrmion would move along the C channel when θ_H < −θ_C, that is,

The Skyrmion would move along the B channel when −θ_C < θ_H < θ_C, that is,

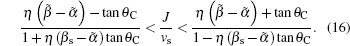
In this work, the Skyrmion dynamics under an electric current and a thermal gradient in a metallic chiral magnet is studied. Based on the LLGS equation the dynamic equation for Skyrmions is derived. The results show that the Hall angle can be controlled when magnonic current is perpendicular to electric current. Using this property, the proposed design of the Skyrmion valve in confined geometries can be used to move Skyrmions along a desired channel. Besides, a new method of measuring dissipative correction of thermomagnonic torque is provided.