Cite this Article
Yang Rong, Tang Bin, Gao Tao, Ao BingYun. Hybrid density functional study on lattice vibration, thermodynamic properties, and chemical bonding of plutonium monocarbide. Chinese Physics B, 2016, 25(6): 067106  
Permissions
Hybrid density functional study on lattice vibration, thermodynamic properties, and chemical bonding of plutonium monocarbide
Yang Rong1, 2, Tang Bin3, Gao Tao1, †, , Ao BingYun4, ‡,
Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China
College of Materials Science and Engineering, Chongqing Jiaotong University, Chongqing 400074, China
Institute of Finance & Trade, Chongqing City Management College, Chongqing 401331, China
Science and Technology on Surface Physics and Chemistry Laboratory, P. O. Box 718-35, Mianyang 621907, China

 

† Corresponding author. E-mail: gaotao@scu.edu.cn

‡ Corresponding author. E-mail: aobingyun@caep.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 21371160 and 21401173).

Abstract
Abstract

Hybrid density functional theory is employed to systematically investigate the structural, magnetic, vibrational, thermodynamic properties of plutonium monocarbide (PuC and PuC0.75). For comparison, the results obtained by DFT, DFT + U are also given. For PuC and PuC0.75, Fock-0.25 hybrid functional gives the best lattice constants and predicts the correct ground states of antiferromagnetic (AFM) structure. The calculated phonon spectra suggest that PuC and PuC0.75 are dynamically stable. Values of the Helmholtz free energy ΔF, internal energy ΔE, entropy S, and constant-volume specific heat Cv of PuC and PuC0.75 are given. The results are in good agreement with available experimental or theoretical data. As for the chemical bonding nature, the difference charge densities, the partial densities of states and the Bader charge analysis suggest that the Pu–C bonds of PuC and PuC0.75 have a mixture of covalent character and ionic character. The effect of carbon vacancy on the chemical bonding is also discussed in detail. We expect that our study can provide some useful reference for further experimental research on the phonon density of states, thermodynamic properties of the plutonium monocarbide.

PACS: 71.27. + a;63.20.D–;74.25.Bt
Keyword:hybrid functional;DFT + U, plutonium monocarbide
1. Introduction

Plutonium monocarbide has been a subject of intense interest in recent years, owing to its applications in advanced types of fast reactors. Compared with oxide fuels, it has many advantages. First, its very good thermal conductivity fits the important technological requirements for advanced reactors for higher operating temperatures. Second, plutonium monocarbide with the rock-salt structure is stable in a large domain of nonstoichiometry at high temperature, and its fusion temperature is high. Finally, high burn-up value (10% or more) can be obtained, since plutonium carbides contain a high concentration of metallic elements. These advantages can explain this interest in plutonium monocarbide. As is well known, plutonium monocarbide is a non-stoichiometric compound with the fcc Nacl-type structure.[1] PuC easily forms a defect structure with some of its carbon atom lattice sites vacated. We select PuC0.75 as a defect structure to be investigated. In order to properly utilize carbide fuels in a reactor, their phase relationships and physical properties must be well understood. Of all the physical properties, the need for reliable thermodynamic data on carbide fuels is well recognized by both the engineer and the scientist. The vibrational properties are critical for understanding phase stability and thermal transport. So this work is concerned with the vibrational, thermodynamic properties of plutonium monocarbide (PuC and PuC0.75). Additionally, the investigations of chemical bonding properties of PuC and PuC0.75 from theoretical viewpoint are indispensable to their applications in the nuclear industry.

Experimental studies on the plutonium-bearing materials are challenging because of their toxic and radioactive nature. Thus, theoretical predictions appear to be especially important for plutonium monocarbide. However, the 5f-electron localization phenomena pose a considerable challenge to the theoretical research. To correctly describe the strong electron–electron interactions of f-electron systems, the traditional density functional theory (DFT), DFT plus the Hubbard U[2,3] (DFT + U), dynamical mean field theory (DMFT),[4] and hybrid density functional[5,6] have been developed. DFT + U which has been widely used depends on the Hubbard correction term. The value of Ueff must be tuned to obtain a better description of different properties. In Pu-based compounds, a value of 4 eV for Ueff was generally adopted.[7–9] Hybrid functional method does not contain any system-dependent parameters, but it needs high computational resources and times. In this work, we present results by using hybrid functionals and DFT + U.

Comparing with plutonium oxides, relatively few studies focus on plutonium carbides. Among plutonium carbides, PuC is most studied, and the studies on non-stoichiometric compound are more scarce. Experimentally, the data of structural parameters can be obtained. Experimental work[10] revealed that plutonium monocarbide undergoes a magnetic phase transition at ≈ 100 K, leading to a simple antiferromagnetic structure with Pu along the (0.0,1) direction. The observed valence-band spectra of Pu carbides were obtained by Gouder et al.[11] The heat content (enthalpy) of PuC above 298 K was measured with an isothermal drop calorimeter by Kruger and Savage.[12] In theory, some progress has been made in the ground-state properties of plutonium monocarbide. The structural, electronic and magnetic properties of PuC were investigated by Wen et al.[9] Havela et al.[13] studied the magnetic properties of PuC by LDA + U calculations. Petit et al.[14] investigate the ground-state valency configuration of Pu ions in PuC by using the self-interaction corrected local spin-density approximation. However, to our knowledge, no data of phonon spectrum are available in the literature. The accurate determination of phonon spectrum can help us to acquire thermodynamic properties such as the Helmholtz free energy ΔF, internal energy ΔE, entropy S, and constant-volume specific heat Cv. In addition, the investigation of chemical bonding has not been included in the previous studies. Hence, we calculate the lattice vibrations, thermodynamic properties and chemical bonding of PuC and PuC0.75. Our investigations, especially for nonstoichiometric compound (PuC0.75) are of great significance.

In this work, we first investigate the crystal structures and magnetic properties of PuC and PuC0.75, and compare the results with experimental data to check whether hybrid functional method is suitable for PuC and PuC0.75. Then, phonon-dispersion curves of PuC and PuC0.75 are obtained, the Raman and infrared active modes at Γ point are further assigned and presented. Next, the thermodynamic properties including ΔF, ΔE, S, and Cv are predicted for PuC and PuC0.75. And finally, the chemical bonding properties of PuC and PuC0.75 are discussed in detail.

The rest of this paper is organized as follows. In Section 2 we describe our computational method and details, and the results are presented and discussed in Section 3. This paper is ended with conclusions in Section 4.

2. Computational method

All our calculations are performed by using the full potential linearized augmented plane wave (FP-LAPW) method as implemented in the all electron WIEN2K code.[15,16] In the exchange–correlation functional used are GGA Perdew–Burke–Ernzerhof (PBE) formalism[17] and the local spin-density approximation (LSDA).[18] In the LSDA + U[19] calculations, the effective Hubbard U is 4.00 eV, which is used by Wen et al.[9] In the hybrid scheme, the PBE0 and Fock-0.25 hybrid functionals are employed. For PBE0 hybrid functional,[20,21] the exchange-correlation energy is

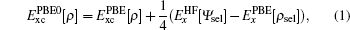
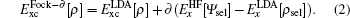
where Ψsel and ρsel refer to the wave function and the corresponding electron density of the selected electrons, respectively. For PBE0, a fraction (1/4) of HF exchange replaces the GGA (PBE) exchange but only for the selected electrons. The exchange–correlation energy of Fock-α hybrid functional[22] is

The form of Eq. (2) is the same as that of Eq. (1), except LDA replacing PBE. In this work, we use α = 0.25 for the fraction, giving functional Fock-0.25.

In our calculations of PuC, a supercell consisting of 4 Pu atoms and 4 C atoms is used. When one C atom is replaced by a vacancy, it forms C-deficient compound PuC0.75. We should mention that the experimentation[1] confirms that the C-deficient compound has the fcc Nacl-type structure.

The muffin-tin radii have been chosen to be 2.3 a.u. and 1.6 a.u. (The unit a.u. is short for atomic unit) for Pu and C atoms, respectively. The parameter RMTKMAX = 8.5, where RMT is the smallest atomic sphere radius and KMAX is the plane wave cutoff parameter. The Brillouin zone is sampled with 100 k-points. The charge convergence is set to be 0.001 e, the total energy convergence is set to be 0.001 Ry (1 Ry = 13.6056923(12) eV), and the force convergence is set to be 0.001 Ry/a.u. In the antiferromagnetic (AFM) calculations, we take the 1k (collinear) order. The spins of Pu atoms change sign along the oz axis.

3. Results
3.1. Crystal structure and magnetic properties

We calculate the total energies for a set of different atomic volumes to determine the optimized lattice constants. The bulk modulus is obtained from fitting to Murnaghan’s equation of state.[23] The band gaps, the total magnetic moment and the differences in total energy between ferromagnetic (FM) and AFM states (ΔE = EFM − EAFM) are also obtained. All results are listed in Table 1.

Table 1.

Complication of data on FM and AFM states of PuC and PuC0.75: lattice constant a0, total magnetic moment μtot, bulk modulus B0, ΔE = EFM − EAFM, and band gap (eV). The Hubbard parameter U is 4.0 eV.

.

The known experimental finding is that at room temperature the lattice parameter increases from a value of 4.953 Å to 4.973 Å as the carbon content increases from the hypo-to hyper-stoichiometric composition.[24–29] For stoichiometric PuC, the measured lattice parameter is 4.965 Å.[24] From Table 1, our calculated lattice constants of FM states are larger than those of AFM states for both PuC and PuC0.75. The optimized lattice constants in AFM states are closer to the experimental values, which means that the ground states of PuC and PuC0.75 are AFM. Our calculated values of ΔE(= EFM − EAFM) by LSDA + U and Fock-0.25 methods are positive. This also indicates that the AFM state is stabler than the FM state. The conclusion is confirmed by experimental work that an AFM transition occurs at 100 K in plutonium monocarbide.[10] However, LSDA incorrectly predicts an FM ground state of PuC.

Of all the methods, Fock-0.25 yields the very accurate lattice constants. For example, for PuC in the AFM state, the value 4.961 Å deviates from the experimental data only by 0.004 Å. But PBE0 severely overestimates the lattice parameter in FM (or AFM) state. This indicates that GGA (PBE) is not suitable for plutonium monocarbide. When a C atom is removed from PuC to form C-deficient compound PuC0.75, a decrease of lattice constant is found in Table 1. For example, the lattice parameter of PuC0.75 is reduced by about 0.005 Å from Fock-0.25 in the AFM state. It means that the additional removal of a C atom makes lattice contraction. The measured lattice constant increases from 4.953 Å to 4.973 Å as the carbon content increases. So our results are in good agreement with the experimental results.

As expected, the lattice parameter increases as long as the electron correlation (U or hybrid functional) is included. When Hubbard U increases from 0 to 4 eV, the localization of the 5f electrons of Pu will be enhanced, while the cohesion of the crystal is further reduced, which leads to the increase of the lattice constant. Moreover, we consider the effects of spin-orbit coupling (SO). When SO is included, the lattice parameter is reduced slightly in LSDA + U + SO/Fock-0.25 + SO framework compared with that in the LSDA + U/Fock-0.25, which is similar to the Pu–H systems calculated by Guo et al.[8] From the energy differences between the FM and AFM states in LSDA + U + SO/Fock-0.25 + SO framework, the ground states of PuC and PuC0.75 are also AFM. So spin–orbit coupling has little effect on crystal structure and magnetic properties of PuC and PuC0.75. Furthermore, the lattice constants of PuC and PuC0.75 in Fock-0.25 are much closer to the experimental values than those obtained by LSDA + U + SO/Fock-0.25 + SO. Thus, SO is not taken into account in the following calculations.

From our calculated band gaps, both PuC and PuC0.75 are conductors. It is true since plutonium monocarbide is metal. Finally, we compare our results with other theoretical values (HSE[9] and SIC-LSD[14]). We find that our calculated lattice parameters obtained by Fock-0.25 are much better than the others, suggesting that the advantage of the present method (Fock-0.25) over the others for plutonium monocarbide. For the bulk modulus B0, our calculated value 177.40 GPa from Fock-0.25 can be compared with the result 172.00 GPa from SIC-LSD.[14]

On the whole, Fock-0.25 gives the best structural properties and predicts AFM phase, which supplies the safeguard for the following calculations of vibrational and thermodynamic properties of PuC and PuC0.75. For comparison, LSDA + U calculations will be also performed in the following studies. While PBE0 is not adopted in the following calculations, since the optimized lattice parameters are not reproduced well by PBE0.

3.2. Vibrational properties

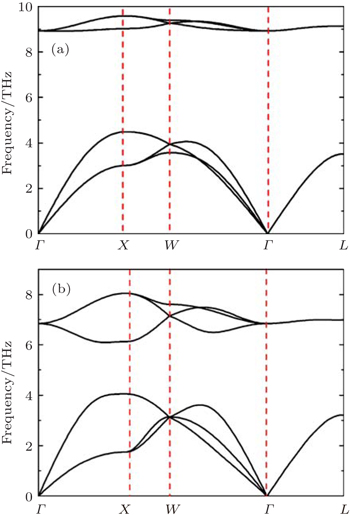
Our phonon calculations are performed by the small displacement method.[30] Since the space groups of PuC and PuC0.75 are Fm-3m (225), PuC and PuC0.75 belong to Oh point group. The high-symmetry points selected in the calculations are Γ(0, 0, 0), X (0.5, 0, 0.5), W (0.5, 0.25, 0.75), and L (0.5, 0.5, 0.5). For stoichiometric PuC, there are two atoms in a primitive cell. Thus, this system contains three acoustic modes and three optical modes, that is, two optical transverse branches and one optical longitudinal branch, two acoustic transverse branches and one acoustic longitudinal branch are included. The phonon dispersion curves of PuC obtained from Fock-0.25 and LSDA + U are shown in Figs. 1(a) and 1(b), respectively. From Fig. 1, we find no imaginary frequencies, which indicates that PuC is dynamically stable at ambient pressure and 0 K. It is obvious that the phonon dispersion curves obtained by Fock-0.25 and LSDA + U methods do not differ greatly. The biggest difference is the value of the gap between the acoustic and optical branch. For LSDA + U, the gap is 2.78 THz, and the gap is 4.43 THz for Fock-0.25. The difference can be explained as follows. In the LSDA + U (Ueff = 4.0 eV) method, the localization of Pu 5f electron is more strengthened, the corresponding contribution to Pu–C covalent bonding is more weakened, while the ionic character is more enhanced, which results in the decrease of lattice vibration energy. On the basis of point group theory, the irreducible representations of the acoustic mode and optical mode in the center of the BZ are: Γacoustic = T1u, and Γoptical = T1u, respectively. Here T1u is infrared-active. The phonon frequencies for infrared-active modes T1u obtained with Fock-0.25 and LSDA + U at Γ point are 297.66 cm−1 and 228.29 cm−1, respectively. These data need to be checked by future experiments. Considering the fact that Fock-0.25 gives the best structural properties, Fock-0.25 framework can describe the dynamical properties of PuC reasonably. The phonon partial densities of states (PPDOSs) of PuC from Fock-0.25 and LSDA + U are plotted in Fig. 2. Since Pu atom is heavier than C atom, the vibration frequency of Pu is lower than that of C atom.

Fig. 1. Calculated phonon dispersion curves from (a) Fock-0.25 and (b) LSDA + U for PuC.
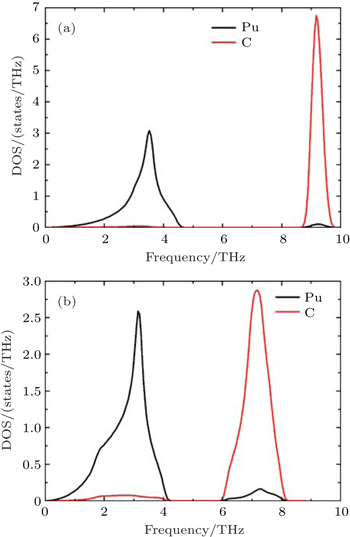Fig. 2. Calculated phonon partial densities of states (PPDOSs) from (a) Fock-0.25 and (b) LSDA + U for PuC.

Now we discuss the lattice dynamical properties of PuC0.75. For simplicity, we only show the results from Fock-0.25. From Fig. 3(a), the calculated phonon dispersion curves have no soft modes, which indicates that PuC is dynamically stable. Since the primitive cell contains 7 atoms, there are 3 acoustic modes and 18 optical ones. According to the group-theoretical analysis, the irreducible representations at the BZ are Γacoustic = T1u and Γoptical = 4T1u + 2T2u. Here T1u is infrared-active and T2u is silent mode. The calculated phonon frequencies at Γ point are listed in Table 2. Figure 3(b) shows the PPDOSs of PuC0.75. It is very easy to observe that along the frequency axis, there are two frequency gaps whose widths are 5.13 THz and 1.33 THz. And we note that the PPDOSs of each Pu atom distinguish each other and the PPDOSs of each C atom are almost the same as those of PuC0.75. The reason is that the crystal symmetry is destroyed when a C atom is removed from PuC.

Fig. 3. Calculated (a) phonon dispersion curves and (b) partial density of phonon states (PPDOSs) from Fock-0.25 for PuC0.75.
Table 2.

Calculated phonon frequencies (in cm−1) and the assignment of the infrared-active and silent modes at Γ point of PuC0.75.

.

To our knowledge, there are currently no experimental or theoretical data for the vibrational properties of PuC and PuC0.75. We hope our results can provide useful reference for the further research on the vibrational properties of PuC and PuC0.75.

3.3. Thermodynamic properties

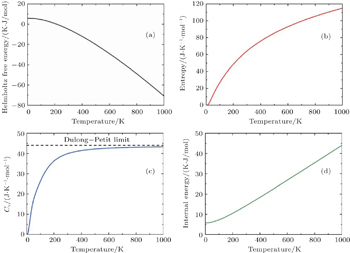
Thermodynamic properties of solid materials can be determined by the calculated phonon density of states in the quasiharmonic approximation (QHA). The expressions of the Helmholtz free energy ΔF, internal energy ΔE, entropy S, and constant-volume specific heat Cv are given, respectively, by[31]

where w is the phonon frequency, g(w) is the normalized phonon DOS, N is the number of unit cells, kB and ℏ refer to the Boltzman constant and reduced Planck constant, respectively. At zero temperature, the ΔF and ΔE can be expressed as . Figure 4 shows the computed ΔE, ΔF, S, and Cv of PuC each as a function of temperature in the Fock-0.25 framework. We can find that ΔE0 = ΔF0 = 7.4 K·J/mol and ΔE increases almost linearly with temperature rising. From Fig. 4(b), the vibrational entropy curve increases smoothly with the increase of temperature due to the vibrational frequency increasing with temperature. At high temperature (over 800 K), our calculated Cv tends to be a constant of 49.6 J/(K/mol), which almost approaches to the Dulong–Petit limit. The Dulong–Petit law[32] is Cv = 3N*R, where N is the number of atoms and R is the gas constant. For PuC, there are two atoms in one formula, which means that the theoretical value should be 49.9 J/(K/mol). Obviously, the deviation between our value and theoretical value is only 0.6%.

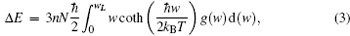
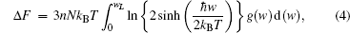
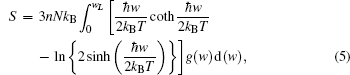
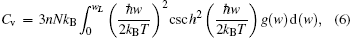
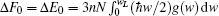
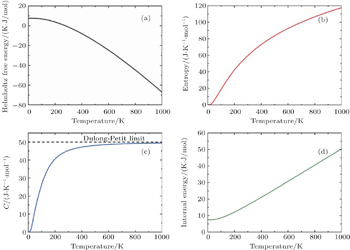Fig. 4. Calculated (a) the Helmholtz free energy ΔF, (b) the entropy S, (c) the constant-volume specific heat Cv, and (d) the internal energy ΔE of PuC in the Fock-0.25 framework.

The observed changes in enthalpy of PuC with temperature rising are listed in Table 3, along with our calculated ones. Here, the change in enthalpy is acquired by the equation ΔH = ΔE + PΔV, where E refers to the internal energy, P the pressure, and V the volume.[33] In solid and liquid phases, the change in term PΔV is very small compared with in term ΔE. And we set the equilibrium pressure to be zero. So, ΔH ≈ ΔE. Comparing the data in Table 3, our calculated ΔH from Fock-0.25 and LSDA + U are in good agreement with the experimental results. The slightly larger deviation of ΔH under high temperature may be due to the limitation of the QHA. In our calculations, all the vibrational eigenvalues are obtained at T = 0 K. With the increase of temperature, the volume dependence of phonon free energy changes, then the equilibrium volume changes with temperature. The high-order anharmonicity at high temperature may become more prominent than at low temperature for Pu monocarbide.

Table 3.

Calculated values of H–H298 (K·J/mol) and the corresponding experimental data of PuC.

.

Listed in Table 4 are our calculated ST–S298 (J/(K/mol)) and heat capacity (J/(K/mol)) of PuC using QHA, comparison with previous theoretical data.[12] These quantities are calculated for a temperature of 1900 K, which is 50 K below the melting point of PuC.[34] Cp and Cv are related by the following equation[35]

where α is the volume thermal expansion coefficient, B is the bulk modulus, V is the volume, and T is absolute temperature. Kruger and Savage[12] calculated Cp according to the equation Cp = 13.08 + 11.44 × 10−4 T − 3.232 × 105T−2 suggested by Maier and Kelley.[36] From Table 4, the entropy difference ST–S298 obtained by us can also be compared with other theoretical results. Besides the limitation of the QHA, we only consider the vibration entropy and ignore the electronic contribution to the entropy in our calculations, which leads to the increase of difference between our data and the values of Kruger and Savage as temperature rises. Certainly, the Cv values are different from the Cp values at high temperatures according to Eq. (7).

Table 4.

Our calculated values of ST–S298 (J/(K/mol)) and heat capacity (J/(K/mol)) of PuC, along with other theoretical values.

.

For PuC0.75, we also investigate its thermodynamic properties. In Table 5 listed are our calculated values of S, H–H298, and Cv at selected temperatures. Several authors have measured the absolute entropies of nonstoichiometric plutonium carbides at 298.15 K. Their results are 18.2,[37] 21.2,[38] 15.3,[39] and 17.2[40] cal/(mol/K). The value estimated by us is 15.3 cal/(mol/K) in Fock-0.25 scheme. So our calculated value agrees reasonably with the experimental data. The curves of ΔE, ΔF, S, and Cv versus temperature are shown in Fig. 5. The Cv of PuC0.75 also follows the Debye model, and is also close to the classic limit (43.6 J/(K/mol)) which is called Dulong–Petit’s law[32] at high temperatures (over 800 K).

Table 5.

Our calculated values of H–H298 (K·J/mol), S (J/(K/mol)), and Cv (J/(K/mol)) of PuC0.75.

.
Fig. 5. Calculated (a) the Helmholtz free energy ΔF, (b) the entropy S, (c) the constant-volume specific heat Cv, and (d) the internal energy ΔE of PuC0.75 in the Fock-0.25 framework.
3.4. Chemical bonding

In this section, we will analyze the Pu–C bonds of PuC and PuC0.75. The charge densities and the difference charge densities along the (001) plane of PuC and PuC0.75 are shown in Figs. 6 and 7, respectively. The difference charge density is obtained from the equation[41]

where ρ is the valence-electron charge density. Figures 6(a) and 7(a) both show that the highest density charge piles up in the immediate vicinity of the nuclei, while the charge densities are relatively low in the interstitial regions. It reflects that most of the electrons are firmly bound up around atomic nuclei, and only a few valence electrons can escape from their bondage. For the nearest Pu–C atoms, the charge density distribution is largely deformed toward their bonds, which implies significant covalent character in the bonding of Pu and C atoms. This is associated with the hybridization between Pu-6d and C-2p states, which can be seen from the partial densities of states (Fig. 8). In Figs. 6(b) and 7(b), the orange zone and blue zone represent the gain of charge and the loss of charge respectively. It is clear that a great quantity of charges of Pu atoms move to C atoms for PuC and PuC0.75. So, the bonding between Pu and C atoms also has an ionic character. Compared PuC with PuC0.75, Pu ions in PuC0.75 are ionized somewhat less than Pu ions in PuC. This can be explained in the following. That one C atom is replaced by a vacancy means the breaking of some Pu–C bonds, which leads to the growing of plutonium states in this region and their delocalization toward Pu–Pu bonds near the lattice defect.

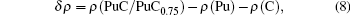
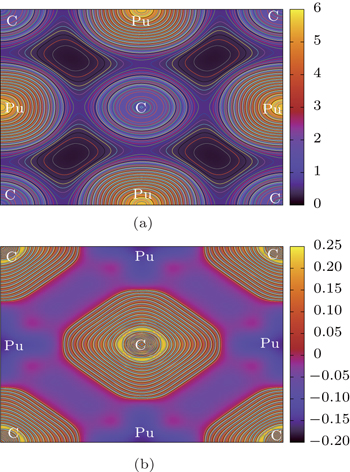Fig. 6. Contour plots of (a) charge density and (b) charge density difference along the (001) plane in Fock-0.25 calculations for PuC.
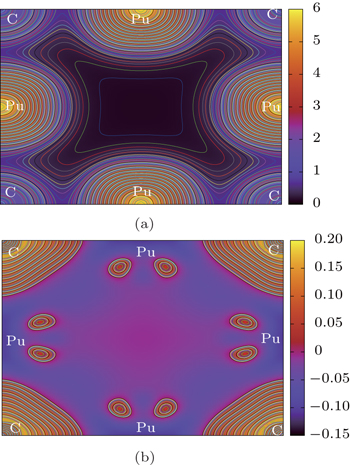Fig. 7. Contour plots of (a) charge density and (b) charge density difference along the (001) plane in Fock-0.25 calculations for PuC0.75.
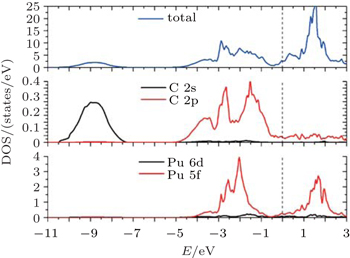
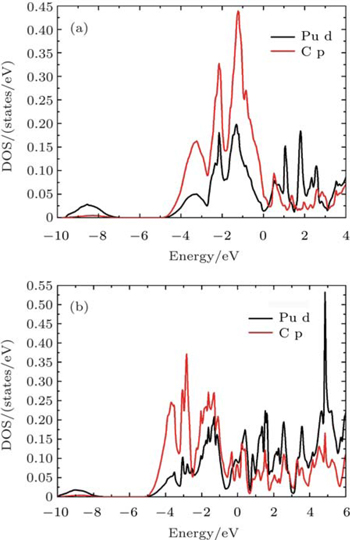Fig. 8. Partial densities of states for the Pu d and C p of (a) PuC (b) PuC0.75 in Fock-0.25 calculations.

The charge transfer between the Pu atom and the C atom is quantified by the Bader charge analysis.[42] As is well known, Pu atom has 16 electrons outside the core, and C atom has 4 electrons outside the core. All results are listed in Table 6. When one C atom is replaced by a vacancy, the crystal symmetry is destroyed. So for PuC0.75, Pu atoms are divided into two categories: one is near the vacancy which is marked as Pu2, the other is far from the vacancy which is denoted as Pu1. From Table 6, each Pu atom losses 1.14|e| and the charge of 1.14|e| is transferred to C atom in PuC system. The result suggests that any directional bonding of the C atom to Pu atom is ionic and small. While for PuC0.75, one Pu atom far from the vacancy (Pu1) still losses 1.14|e|, each Pu atom near the vacancy (Pu2) losses 0.83|e|, and these charges are transferred to three C atoms. Thus, the ionic character of the PuC0.75 system is weaker than that of the PuC system near the vacancy, which is similar to the result of the difference charge densities (Fig. 6(b) and Fig. 7(b)) as mentioned above.

Table 6.

Calculated bader charges (QB) and bader volumes (VB) for AFM PuC and AFM PuC0.75 in Fock-0.25 framework.

.

According to the charge densities and the difference charge densities, the partial densities of states, the Bader charge analyses for PuC and PuC0.75, we can reach the following conclusion. (i) Mixtures of covalent and ionic character are present in the Pu–C bonds of PuC and PuC0.75. (ii) The ionic character is stronger than the covalent character in the PuC system. (iii) Near the vacancy, Pu ions in PuC0.75 are ionized somewhat less than Pu ions in PuC, and the ionic character is weaker than the covalent character in the PuC0.75 system. (iv) Pu–Pu bonds near the vacancy are strengthened.

The observed valence-band spectra[11] of PuC1−x are characterized by the fingerprint of a triplet of sharp features, located at (or slightly below) the Fermi energy, 0.50 eV and 0.85 eV. And the spectra are dominated by the 5f character. So at the end of this section, we give the total and partial densities of states for PuC0.75 in Fock-0.25 scheme for comparison. From Fig. 9, our calculated spectrum ranging from 0 eV to 3 eV almost originates from Pu atoms, and the DOS of Pu atoms is almost dominated by the 5f partial DOS. Furthermore, our spectra also have three sharp peaks which are located at −0.04, 0.34, and 0.88 eV (see Fig. 9). Thus, our results relatively well describes the observed feature of three sharp peaks.

Fig. 9. Total and partial densities of states for PuC0.75 in Fock-0.25 calculations.
4. Conclusions

The lattice vibrations, thermodynamic properties and chemical bondings of PuC and PuC0.75 are systematically studied by using first-principle calculations. Since PuC and PuC0.75 are strongly correlated materials, DFT + U and hybrid density functional which replaces part of the DFT exchange by 25% exact HF exchanges are employed. The optimized lattice constants are in good agreement with known experimental data. LSDA + U and Fock-0.25 successfully predict the correct ground states of AFM PuC and PuC0.75 reported in experiments. We adopt the LSDA + U and Fock-0.25 to study the phonon dispersion curves and the corresponding PPDOSs of PuC and PuC0.75. The infrared active and silent modes at Γ point are further assigned. On the basis of the phonon DOS, we also systematically predict the thermodynamic properties of PuC and PuC0.75. The calculated values of H–H298, ST–S298, and S are in reasonably agreement with the experimental or theoretical values. The present results indicate that our computational methods are feasible and our prediction of the dynamical properties is believable. Through the charge densities, the difference charge densities, the partial densities of states, and the Bader charge analyses, we also carry out systematical studies of chemical bonding. We find that the mixtures of covalent and ionic character are present in the Pu–C bonds of PuC and PuC0.75. That one C atom is replaced by a vacancy leads to the growing of plutonium states in this region and their delocalization toward Pu-Pu bonds near the lattice defect. We expect that our work can provide some valuable information about the plutonium monocarbide for further experimental investigations.

Reference
1Zachariasen W H1949The Crystal Structure of Plutonium Nitride and Plutonium Carbide, The Transuranium Elements, National Nuclear Energy Series. IV–14BNew YorkMcGraw-Hill Book Co., Inc.1448
2Anisimov V ISolovyev I VKorotin M ACzyzyk M TSawatzky G A 1993 Phys. Rev. 48 16929
3Solovyev I VDederichs P HAnisimov V I 1994 Phys. Rev. 50 16861
4Shim J HHaule KKotliar G 2007 Nature 446 513
5Becke A D 1993 J. Chem. Phys. 98 1372
6Becke A D 1993 J. Chem. Phys. 98 5648
7Wang B TZhang P 2011 Chin. Phys. Lett. 28 047101
8Guo YAi J JGao TAo B Y 2013 Chin. Phys. 22 057103
9Wen X DMartin R LScueria G ERudin S PBatista E R 2013 J. Phys. Chem. 117 13122
10Green J LArnold G PLeary J ANereson N G 1967 J. Nucl. Mater. 23 231
11Gouder THavela LShick A BHuber FWastin FRebizant J 2007 J. Phys.: Condens. Matter 19 476201
12Kruger O LSavage H 1964 J. Chem. Phys. 40 3324
13Havela LShick AGouder T 2009 J. Appl. Phys. 105 07E130
14Petit LSavane ASzotek ZTemmerman W MStoks G M 2009 Phys. Rev. 80 045124
15Blaha PSchwarz KMadsen G K HKvasnicka DLuitz J2011WIEN2k − – an Augmented Plane Wave + Local Orbitals Program for Calculating Crystal PropertiesAustriaKarlheinz Schwarz Technische Universität Wien
16Singh D J1994Planewaves, Pseudopotentials and the LAPW MethodBostonKluwer Academic
17Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
18Vosko S HWilk LNusair M 1980 Can. J. Phys. 58 1200
19Liechtenstein A IAnisimov V IZaanen J 1995 Phys. Rev. 52 5467
20Ernzerhof MScuseria G E 1999 J. Chem. Phys. 110 5029
21Adamo CBarone V 1999 J. Chem. Phys. 110 6158
22Moreira Ide P RIllas FMartin R L 2002 Phys. Rev. 65 155102
23Murnaghan F D 1944 Proc. Natl. Acad. Sci. USA 30 244
24Benedict UDufour CScholten O 1978 J. Nucl. Mater. 73 208
25Mulford R N REllinger F HHendrix G SAlbrecht E D1961The Plutonium–Carbon System, Plutonium1960LondonCleaver-Hume Press Ltd.301
26Rosen SNevitt M VMitchell A W 1963 J. Nucl. Mater. 10 90
27Kruger O L 1963 J. Am. Ceram. Soc. 46 80
28Pascard R1961E’tudes preliminaires sur le systeme plutonium-carbone et les solutions solides carbure d’uranium-carbure de plutonium, in Powder Metallurgy In the Nuclear Age. Plansee ProceedingsMetallwerk Plansee AC, Reutte/Tyrol (1C62))387
29Burnham J BSkavdahl R EChikalla T D1964Plutonium Bearing Refractory Carbides, Carbides in Nuclear EnergyVol. 1LondonMacmillan and Co. Ltd.51
30Alfè D 2009 Comput. Phys. Commun. 180 2622
31Lee CGonze X 1995 Phys. Rev. 51 8610
32Petit A TDulong P L1819Annales. de. chimie. et. de. physique. (in French)10395
33Limpijumnong SJungthawan S 2004 Phys. Rev. 70 054104
34Mulford R N REllinger F HHendrix G SAlbrecht E D1961in Plutonium1960LondonCleaver-Hume Press Ltd.301
35Wang RWang S FWu X ZSong T T 2012 Int. J. Thermophys. 33 300
36Maier C GKelley K K 1932 J. Am. Chern. Soc. 54 3243
37Rand M HStreet R S1964Anomalous Thermal Expansions in the Plutonium Monocarbide Region, Carbides in Nuclear EnergyVol. 1.LondonMacmillan and Co. Ltd.108
38Rand M HStreet R S1962 High Temperature X-ray Diffraction Studies, Part 3, Plutonium Nitride and Plutonium SesquicarbideAERE-M-73
39Leary J AThomas R LOgard A EWorm G C1964Thermal Conductivity and Electrical Resistivity of UC, (U, Pu)C, and PuC. Carbides in Nuclear Energy1LondonMacmillan and Co. Ltd.365
40Moser J BKruger O LThermal Diffusivity of Aetinide Compounds, Thermal Conductivity, Proceedings of Seventh Conference302
41Hector L GHerbst J FCapehart T W 2003 J. Alloys Compd. 353 74
42Bader R F W1990Atoms in molecules: a uantum theoryNew YorkOxford University Press