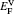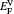† Corresponding author. E-mail:
Project supported by National Basic Research Program of China (Grant No. 2011CB606402) and the National Natural Science Foundation of China (Grant No. 51071091).
Density functional theory calculations in conjunction with the climbing images nudged elastic band method are conducted to study the diffusion phenomena of the Ni-based single crystal superalloys. We focus our attention on the diffusion processes of the Ni and Al atoms in the γ and γ’ phases along the direction perpendicular to the interface. The diffusion mechanisms and the expressions of the diffusion coefficients are presented. The vacancy formation energies, the migration energies, and the activation energies for the diffusing Ni and Al atoms are estimated, and these quantities display the expected and clear transition zones in the vicinity of the interface of about 3–7 (002) layers. The local density-of-states profiles of atoms in each (002) layer in the γ and γ’ phases and the partial density-of-states curves of Re and some of its nearest-neighbor atoms are also presented to explore the electronic effect of the diffusion behavior.
Ni-based superalloys represent a very important class of engineering material, and they have widespread applications in critical components within the gas turbine engines used for jet propulsion and electricity generation. This is due to their low specific weight, high melting point and good chemical stability.[1,2] It is well-known that these alloys are hardened by γ′ precipitates (L12 structure) which are coherently embedded in a nickle solid solution γ matrix (face-centered cubic (fcc) structure). The γ′ cuboids are generally aligned along ⟨001⟩ lattice directions and have a cube-cube relationship with the matrix γ phase.[3,4]
The structure of the interface plays an important role in determining properties in multiphase systems.[5–7] Several experimental and theoretical studies of the interface between an ordered precipitate and disordered matrix in a Ni-based superalloy indicated that the interface is not abruptly changed on an atomic scale but confirmed the existence of a structural transition zone across the interface. Srinivasan et al.[8] have determined a clear order–disorder transition zone at the γ/γ′ interface of Ni based superalloy Rene’ 88 DT where the long-range order decreases roughly over 6–8 atomic {002} plane (approximately 10 Å to 13 Å). They also conducted a three-dimensional atom probe (3DAP) experiment on the same sample, and the results exhibited an order-disorder transition zone ∼ 4–6 {002} plane wide (7 Å–10 Å). Mishin[9] obtained the atomic structure of the interface by grand canonical Monte Carlo simulations on a 1536-atom supercell containing a coherent (100) γ/γ′ interface, and the results showed that the long-range order decays gradually over 4-6 (200) layers around the interface. Kitashima et al.[10] reported that the segregation of Al in the γ/γ′ interface region extends over 10 atomic layers in Ni–Al–Mo system.
Abundant observations indicated that extensive diffusion occurs across the γ/γ′ interface.[11,12] As is well known, various solid-state reactions, phase transformation, microstructural changes and the process of mass transport occurring in materials are diffusion controlled.[13,14] Watanabe et al.[15] pointed out that the main factors controlling the stability of the supercell are lattice misfit, interface structure between the two phases and diffusion phenomena across the interface. As a result, it is reasonable to assume that there might be a close relationship between the interfacial transition zone and the diffusional phenomena across the γ/γ′ interface.
Alloying elements, such as Co, Cr, Mo, Re, Ru, Ta, W, etc. are added to the Ni-based superalloys to enhance the high-temperature properties. A considerable body of experimental research indicates that, among the different alloying additions, Re imparts the most potent creep strengthening.[16] Murakami et al.[17] and Warren et al.[18] showed that there was a Re enrichment in the γ matrix around the γ/γ′ interface. Therefore, the Re alloying could interfere with the diffusion process at the interface and might act as an efficient obstacle for the atomic movement.
The understanding of the diffusion mechanism, improved analysis, theory and modelling are needed. In the present paper, we try to identify the affected areas of the clean and Re-doped γ/γ′ interfaces from a diffusional point of view. We focus our attention on the vacancy mediated diffusions of Ni and Al atoms in the γ and γ′ phases along the direction perpendicular to the γ/γ′ interface. The vacancy formation energy, the migration energy and the activation energy at 0K are estimated by using density functional theory calculations in conjunction with the climbing images nudged elastic band method. The trend of the variations of the above three quantities across the interface could determine clear influence areas of the phase boundary. The results are followed by an explanation from the electronic structures.
The rest of this paper is organized as follows. In Section 2 we describe the theoretical model for the four cases of the vacancy-mediated diffusion. In Section 3, we explain our computational details. In Section 4 we give our calculated results and some further discussion.
In the diffusional phenomena across the γ/γ′ interface, the processes of Al atoms diffusing out of the γ′ phase and then into the γ phase and Ni atoms diffusing out of the γ phase and then into the γ′ phase can be decomposed into four cases, i.e., the diffusion of Al atoms in the γ′ phase, the diffusion of Al atoms in the γ phase, the diffusion of Ni atoms in the γ phase, and the diffusion of Ni atoms in the γ′ phase. In what follows, we will discuss the four diffusion mechanisms separately.
The diffusion of Ni atoms in the γ phase apparently belongs to the self-diffusion process which is mediated by vacancy-type defects in metals.[19] Its self-diffusion coefficient DNi-γ can be described by an Arrhenius relation[20]
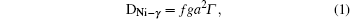
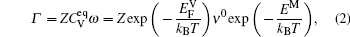
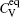
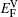
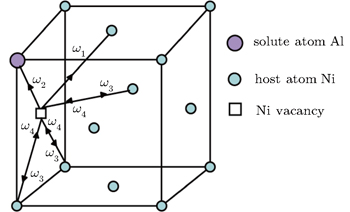 | Fig. 1. Five-frequency model in the case of the fcc γ phase with a dilute solute Al atom. The arrows indicate the direction of the vacancy jump. |
With Eqs. (
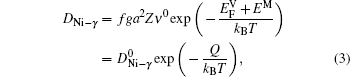
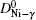
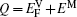
The diffusion of Al atoms in the γ phase belongs to the vacancy-mediated solute diffusion category, which can be analyzed by employing the transition state theory within the Lidiard’s five-frequency exchange model.[21,22] Diffusion coefficient DAl–γ can be expressed as
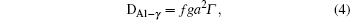
An exact expression for f was derived by Manning[24] as follows:

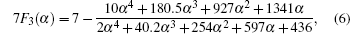
In Eq. (

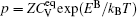
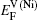

Therefore the diffusion coefficient DAl–γ can be expressed as

The L12-type ordered structure on which Ni3Al is based can be decomposed into two sublattices. The major element Ni occupies the face-center sites, constituting the α sublattice, and those of the minor element Al occupy the cube-corner sites, constituting the β sublattice. While an α sublattice site is coordinated with eight α sites and four β sites, a β site is surrounded entirely by α sites.[25] Ni diffusion can occur by exchange of an Ni atom for a neighboring vacancy on the Ni site without creating disorder.[26] Thus, it is quite natural that the diffusion of the majority component Ni in L12 compound Ni3Al is by a sublattice vacancy mechanism. The diffusion coefficient is expressed as

Although a jump of the Al atom to a nearest neighbour site disturbs the ordered arrangement, an antisite Al atom can exchange its position for a vacancy on a neighboring α sublattice without causing further disordering. The review article[28] has shown that Ni3Al belongs to the antistructural-defect type of intermetallics, in which antisite atoms (NiAl and AlNi) are preferentially formed to accommodate the deviations from stoichiometry. In Ni3Al vacancies are mainly formed on the Ni sublattice. So the minority element Al most likely diffuses as antisite atoms in the majority sublattice (NbO lattice).
The diffusion coefficient can be written as
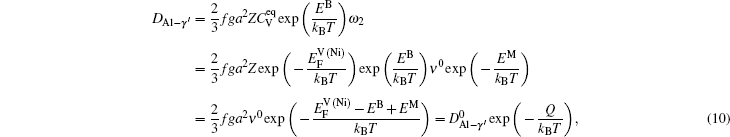
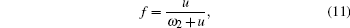
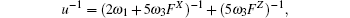
Based on the above discussion, the calculation of the vacancy formation energy energies can be divided into two cases, i.e., 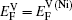
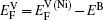

In the first case, the vacancy formation energy is defined as the energy needed to remove one atom j from the host material and place it into a reservoir of the chemical potential μi of the same species. This energy can be written as a function of atomic potential as
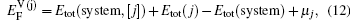
As for the second case, the diffusing Al atoms in the two phases can be treated as impurities. So when calculating the vacancy formation energies, the solute-vacancy interaction should be considered, which can be written as
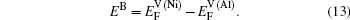
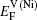
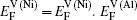
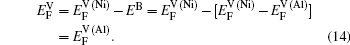
Within a simple Arrhenius relation, as attempt frequencies are relatively similar, the quantity Q largely determines the diffusion properties in close-packed structures. The activation energy for vacancy diffusion can be found by summing together the energy of vacancy formation 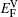
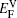
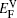
In the present paper, 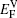
The computational model was a 10 × 2 × 2 unit cell (160 atoms) constructed along the ⟨001⟩ direction as shown in Fig.
From the four diffusion mechanisms mentioned above, we can determine the migration paths of the diffusing Ni and Al atoms, respectively. When Al atom diffuses out of the γ′ phase and into the γ phase, it first diffuses as an antisite atom in the Ni sublattice in the γ′ phase, and then as a solute in the fcc Ni lattice via the first nearest-neighbor Ni-vacancy in the γ phase. When Ni atom diffuses out of the γ phase and then into the γ′ phase, the diffusion process can occur by exchange of a Ni atom for a neighboring Ni-vacancy on the fcc Ni lattice in the γ phase and then in the NbO structure type Ni sublattice.
When considering the diffusion processes of Ni atoms in the γ and γ′ phases and the Al atoms in the γ phase, atom at each atomic site in the respective (002) layer in the model can be viewed as a potent diffusing atom jumping to its nearest-neighbor Ni vacancy; while in the diffusion process of Al atom in the γ′ phase, the position of the antisite AlNi atom should be tested to make sure that it should be placed in a (002) plane of pure Ni or the plane of 50% Ni and 50% Al atoms. An energetic calculation indicates that the antisite AlNi atoms have a preference to be located on the (002) plane with pure Ni atoms as shown in Table
| Table 1. Total energy (in unit eV) of the system with substituting an antisite AlNi atom for the Ni atom in the n-th (002)layer of the model. . |
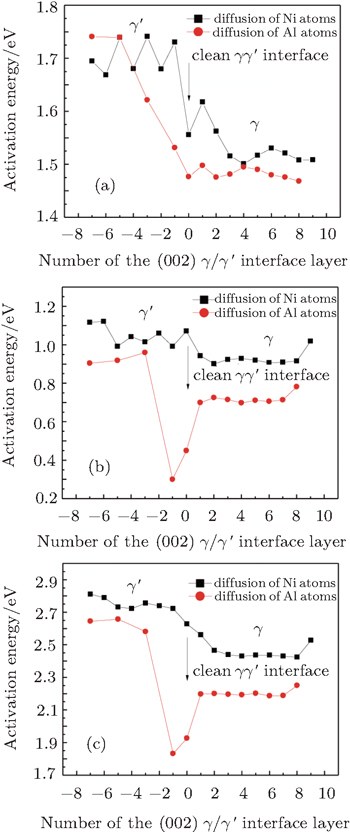
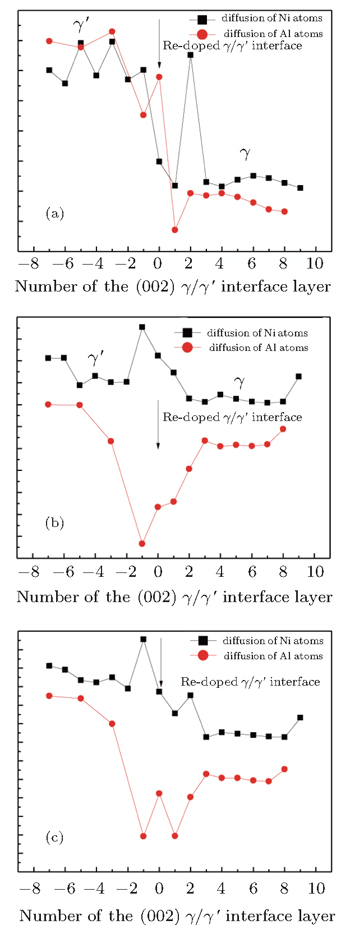
In Figs. 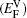
We note that in the vicinity of the γ/γ′ interface, 

It is worthy to point out that the magnitudes of the formation energies of the Ni-vacancies adjacent to the diffusing Al atoms and the corresponding migration energies of the Al atoms in both phases are obviously lower than those of the Ni atoms. This can be attributed to the size effects of the Al atom and Ni atom (Al: 1.43 Å, Ni: 1.24 Å). The Al atom acting as a solute may induce strain on the surrounding atoms. Via the neighboring vacancy, the solute atom would allow itself to relax towards the vacancy and thus go away from the other neighboring atoms. Therefore, the vacancy in a nearest-neighbor position to a large Al atom helps to relieve the strain, producing a strong solute–vacancy binding energy EB, and hence according to Eq. (
We note that between the two phases, the discrepancies in 
We emphasize that the major contribution to the variation of the diffusion activation energy Q across the γ/γ′ interface comes from the variation of the diffusion migration energy EM. Watanabe et al.[15] observed in the experiment that in the Ni/Ni3Al diffusion couple, a γ phase would be transformed from the γ′ phase near the Ni/Ni3Al interface and Kirkendall voids were visible exclusively in this γ phase. The similar formation of Kirkendall voids in the new γ phase was also reported by Janssen[48] and Kawazoe et al.[49] Our calculation results given in Fig.
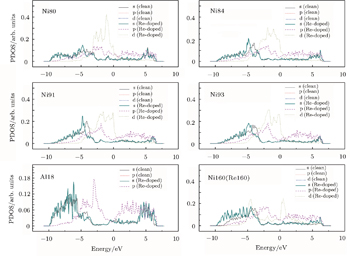
To understand the origin of the affected area of the clean γ /γ′ interface, we present in Figs.
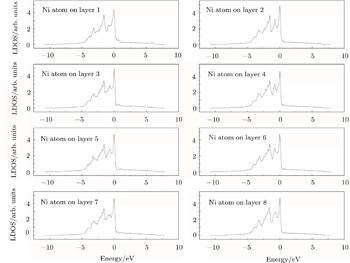 | Fig. 4. LDOSs (in units of states/eV) of some particular Ni atoms on each (002) layer in the γ phase in the clean γ/γ′ interface model. The Fermi level is shifted to zero. |
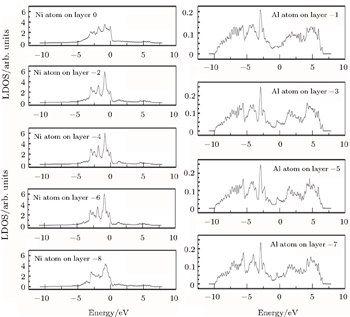 | Fig. 5. LDOSs (in units of states/eV) of some particular Ni or Al atoms on each (002) layer in the γ′ phase in the clean γ/γ′ interface model. The Fermi level is shifted to zero. |
Figure
Further quantitative evaluations of 
Compared with the scenario of the clean γ/γ′ interface, the LDOSs of some corresponding atoms in the γ phase and γ′ phase for the Re-doped interface model are shown in Figs.
 | Fig. 7. LDOSs (in units of states/eV) of some particular Ni atoms on each (002) layer in the γ phase in the Re-doped γ/γ′ interface model. The Fermi level is shifted to zero. |
 | Fig. 8. LDOSs (in units of states/eV) of some particular Ni or Al atoms on each (002) layer in the γ′ phase in the Re-doped γ/γ′ interface model. The Fermi level is shifted to zero. |
To further examine the significant role played by the doping Re at the interface, we investigate the partial density of states (PDOS) curves for Ni160 (Re160) and some of its nearest-neighbor atoms in the clean and Re-doped γ/γ′ interface models. The results are presented in Fig.
First principles quantum-mechanical electronic structure method is used to study the diffusional phenomena of Ni and Al atoms across the clean and Re-doped γ/γ′ interfaces of the Ni-based single crystal superalloys. The diffusional mechanisms of the four circumstances are discussed: the diffusion of Ni atoms in the γ phase belongs to the self-diffusion process which is mediated by the vacancy-type defects, the diffusion of Al atoms in the γ phase can be classified as the vacancy-mediated solute diffusion, and can be analyzed by employing the transition state theory within the Lidiard’s five frequency exchange model, the Ni diffusion in the γ′ phase can occur by exchange of a Ni atom for a neighboring vacancy on the Ni site, and Al atoms in γ′ phase mostly likely diffuse as antisite atoms in the majority Ni-sublattice. The expressions for the vacancy formation energies and the diffusion coefficients for the four cases are also given.
The values of vacancy formation energy 
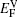

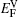
The LDOS profiles suggest that the electronic states of the typical clean γ/γ′ interface are localized within 5 (002) layers of atoms. When Re replaces a Ni atom on the (002) γ/γ′ interface, an obvious change is that for atoms around the interface the LDOS curves at the Fermi level greatly decrease, which means that the transition probability of the electronic states is confined. The PDOS curves show that the Re-d hybridizes strongly with the s, p, d electrons of its nearest-neighbor atoms, showing that the interaction between Re and its adjacent atoms is very strong, which indicates that with the Re doping the stability of the γ/γ′ interface can be increased.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 |