Cite this Article
Sandeep , Rai D P, Shankar A, Ghimire M P, Pradhan Sakhya Anup, Sinha T P, Khenata R, Bin Omran S, Thapa R K. Band-gap engineering of La1−xNdxAlO3 (x = 0, 0.25, 0.50, 0.75, 1) perovskite using density functional theory: A modified Becke Johnson potential study. Chinese Physics B, 2016, 25(6): 067101  
Permissions
Band-gap engineering of La1−xNdxAlO3 (x = 0, 0.25, 0.50, 0.75, 1) perovskite using density functional theory: A modified Becke Johnson potential study
Sandeep 1, †, , Rai D P2, Shankar A3, Ghimire M P4, Pradhan Sakhya Anup5, Sinha T P5, Khenata R6, Bin Omran S7, Thapa R K1
Department of Physics, Mizoram University, Aizawl-796004, India
Department of Physics, Pachhunga University College, Aizawl-796001, India
Department of Physics, University of North Bengal, Darjeeling-734013, India
IFW Dresden e. V., P O Box 270116, D-01171 Dresden, Germany
Department of Physics, Bose Institute, 93/1 Acharya Prafulla Chandra Road, Kolkata 700009, India
Laboratoire de Physique Quantique et de Modélisation Mathématique (LPQ3M), Department de Technologie, Université de Mascara, 29000 Mascara, Algerie, Algeria
Department of Physics and Astronomy, College of Science, King Saud University, P O Box 2455, Riyadh 11451, Saudi Arabia

 

† Corresponding author. E-mail: sndp.chettri@gmail.com

Project supported by the DST-SERB, Dy (Grant No. SERB/3586/2013-14), the UGCBSR, FRPS (Grant No. F.30-52/2014), the UGC (New Delhi, India) Inspire Fellowship DST (India), and the Deanship of Scientific Research at King Saud University (Grant No. RPG-VPP-088). M P Ghimire thanks the Alexander von Humboldt Foundation, Germany for the financial support.

Abstract
Abstract

The structural, electronic, and magnetic properties of the Nd-doped Rare earth aluminate, La1−xNdxAlO3 (x = 0% to 100%) alloys are studied using the full potential linearized augmented plane wave (FP-LAPW) method within the density functional theory. The effects of the Nd substitution in LaAlO3 are studied using the supercell calculations. The computed electronic structure with the modified Becke–Johnson (mBJ) potential based approximation indicates that the La1−xNdxAlO3 alloys may possess half-metallic (HM) behaviors when doped with Nd of a finite density of states at the Fermi level (EF). The direct and indirect band gaps are studied each as a function of x which is the concentration of Nd-doped LaAlO3. The calculated magnetic moments in the La1−xNdxAlO3 alloys are found to arise mainly from the Nd-4f state. A probable half-metallic nature is suggested for each of these systems with supportive integral magnetic moments and highly spin-polarized electronic structures in these doped systems at EF. The observed decrease of the band gap with the increase in the concentration of Nd doping in LaAlO3 is a suitable technique for harnessing useful spintronic and magnetic devices.

PACS: 71.15.–m;71.15.Mb;71.20.Eh;74.62.Dh
Keyword:density functional theory;rare earth aluminates;perovskites;electronic structures
1. Introduction

Compounds with perovskites structure, ABX3 have been the subject of tremendous study due to their diverse applications.[1,2] These applications range from ferro- and piezoelectricity,[3] high electronic and ionic conductivity, diverse magnetism, colossal magnetoresistive effects,[4] to paraelectricity and superconductivity. Single crystalline substrates of RAlO3 alloys such as LaAlO3 and YAlO3 are commonly used for the epitaxy of thin films such as high-temperature superconductor (HTSC), magnetoresistive materials, and GaN films.[5] The effects of doping on the structural, electronic, transport, magnetic, and specific heat properties in 4d perovskites were studied by Zhang et al.,[6] where YAlO3 doped with Yb-2p or V-4p was proposed as a material for the tunable solid-state laser.[7,8] Dielectric permittivities with a ‘high-quality factor’ are of prime interest among rare earth aluminates as they are appropriate for dielectric resonators and substrates for microwave components.[9–11] Recent developments in electronics,[12] optics,[13] and energy conversion applications[14] using the ABO3 type of perovskite compounds have aroused the renewed interest in this field. LaAlO3 is used as the superconductive substrate, superconducting microwave devices, and high k gate oxide to replace silicon dioxide (SiO2) because of its good dielectric characteristics, and thermal properties.[15] At room temperature, LaAlO3 is stable in the rhombohedral structure with R3c space group. By using LaAlO3 as a host material for phosphor where it is doped with transition metals for multiferroic properties, the LaAlO3 turns into an important material to be explored theoretically as well as experimentally.[13] Limited studies have been observed to date on the ferromagnetic and optical properties of the transition metal-doped LaAlO3.[16–18] Hong-Sheng et al. studied the modification of the band gap in β-SiC and reported the change from an indirect to a direct band gap and the decrease of the energy band gap with doping the N-atom for the C atom.[19] Fang et al. have satisfactorily explained the manifestation of an additional absorption peak in the experiments through the doping studies of KMgF3.[20] On the other hand, Lei Shu-Lai et al. have analyzed the weakening of the magnetic moment and magnetic stabilized energy in defective graphene with the hydrogen chemisorbed single-atom vacancy (H-GSV).[21] The decrease in the conductivity of ZnO was predicted and compared with the experimental results by Hou Qing-Yu et al.[22] using the pseudopotential method. Optical properties of TiO doped with two atoms were studied by Wang Qing et al.[23] and Li Shi-Bin et al. studied the effect of polarization doping of AlGaN and predicted that it is a more efficient doping technique.[24] Zylberberg and Ye[25] have studied the dielectric properties of bismuth-doped LaAlO3 to correlate the higher dielectric properties using the high polarizability of the Bi3+ ion with a lone electron pair. Conversely, the structural and optoelectronic properties were studied by Murtaza and Ahmad[26] to explain the shift from the indirect to direct band gap under pressure for LaAlO3. Namjoo et al.[27] have studied the structural, electronic and optical properties of InAs, InSb, and their ternary alloys, InAsxSb1–x (x = 0.25, 0.5, 0.75) within the density functional theory using the modified Becke–Johnson exchange–correlation functional (mBJ-LDA),[28] to report the concentration at which the minimum band gap occurs. In addition, LaAlO3 having the structure, Pm-3m is the stablest structure at its ground state which is favorable for making layered structures and doped structures for technological application. As LaAlO3 and NdAlO3 are already studied and reported as suitable candidates for optoelectronic devices, we attempt to see the significant changes in its electronic structure and phase transitions as we vary the atoms from La to Nd.

2. Method of calculation

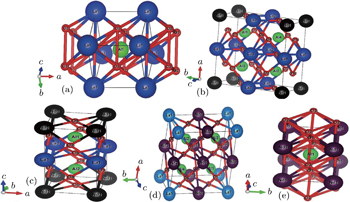
The calculations reported here are carried out using the ab initio full-potential linearized augmented plane wave (FP-LAPW) method[29,30] as implemented in the WIEN2k code,[31] which is one of the most efficient methods of calculating and simulating the ground state properties of materials.[32] Owing to the flexible basis sets in the interstitial and near atomic centers, this method is well suited for open structures with low symmetry. The exchange potential was calculated using the modified Becke–Johnson exchange potential[28–38] and the core states were treated relativistically while the valence states were treated with a scalar relativistic approximation. We employ well-converged basis sets, defined by RminKmax = 7.0, where Rmin is the smallest sphere radius and Kmax is the interstitial plane-wave cutoff. Local orbitals were employed to include the semi-core states and to efficiently linearize the s and p states of the Al and O atoms.[39] A supercell approach[40] was used for doping LaAlO3 with the Nd atoms where it was constructed by substituting one Nd atom in place of the La atom within the unit cell of LaAlO3. We generate 8 La atoms using supercells with the 2 × 2 × 2 configuration and the Nd element is doped at the La site within the unit cell of LaAlO3 as La1−xNdxAlO3. The x compositions are varied such as 25% (2/8), 50% (4/8), 75% (6/8), and 100% (8/8), respectively, as shown in Figs. 1(a)–1(e). When doping, the system undergoes structural phase transition[41] from the space group, Pm-3m to the space group, P4/mmm. The Nd atom has 4f electrons which contribute to the electronic and magnetic feature of the doped system.

Fig. 1. Supercells of the La1−xNdxAlO3 alloys with (a) x = 0% or (0/8), (b) x = 25% or (2/8), (c) x = 50% or (4/8), (d) x = 75% or (6/8), and (e) x = 100% or (8/8).
3. Results and discussion
3.1. Volume, bulk modulus, pressure derivative, and energy

The total energies of the La1−xNdxAlO3 alloys are calculated each as a function of the volume using the full potential linearized augmented plane wave method, where the plots of the calculated total energies versus the reduced volume for these alloys are given in the following Figs. 2(a)–2(e).

Fig. 2. Plots of energy versus volume for La1−xNdxAlO3 alloys with (a) x = 0% or (0/8), (b) x = 25% or (2/8), (c) x = 50% or (4/8), (d) x = 75% or (6/8), (e) x = 100% or (8/8), and (f) plot of the percentage of Nd doping vs volume for the La1−xNdxAlO3 alloys.

The calculated total energies are fitted to the Murnaghan equation of state[42] to determine the ground state properties, such as the equilibrium volume (V), the bulk modulus (B), its pressure derivative (BP), and energy (E). The calculated equilibrium parameters such as V, B, BP, and E, are given in the following Table 1, which also contains the available experimental and theoretical results for comparison with other literatures.[43–45]

Table 1.

Lattice parameters of the La1−xNdxAlO3 alloys, volume, bulk modulus, pressure derivatives, and energy.

.

We find that the volume of the system increases, in general from 1493.2134 a.u.3 at 25% to 1685.0617 (a.u.)3 at 75% doping of Nd in LaAlO3. Also at doping levels of 0%, 50%, and 100%, the volumes are found to be 376.0695 a.u.3, 737.3292 a.u.3, and 359.8465 a.u.3, respectively. A similar trend in the bulk moduli and the respective derivatives of the bulk moduli are also observed as shown in Table 1. Similarly, the bulk moduli of the La1−xNdxAlO3 alloys are found to have a relative increase of 25%, a relative decrease of 8.37%, a relative increase of 710%, and a relative decrease of 14.20%, respectively, from x = 0% to x = 25%, 50%, 75%, and 100% of Nd doping. These changes can be attributed to the size difference or the mismatch of the size of the crystallites with doping and similar trends in the pressure derivatives and energies are also observed in these systems.

3.2. Density of states

For La1−xNdxAlO3 (at x = 0%), the densities of states (DOSs) respectively, in the spin-up and spin-down configurations show similar features where the top of the valence band extending from −3.0 eV to the Fermi level (EF) is dominated mostly by the O-2p state hybridized with the Al-2p state. Conversely, the conduction band which starts from 4.5 eV is mainly composed of the 4f orbital. In all the dopant concentrations, the orbital character of the valence band is primarily derived from the O-2p state orbital.

For La1−xNdxAlO3 (at x = 25%), in both the spin-up and spin-down channels the lower parts of the valence band remain unchanged with contributions from the O-2p state hybridized with the Al-2p states. The Nd-4f state contributions are observed from −0.5 eV to EF in the spin-up configuration with a sharp peak at −0.4 eV as shown in Fig. 3(b). In the spin-up channel, the contribution due to the Nd-4f state is observed between 1.75 eV and 4.0 eV with peaks at 2.9 eV in both spin channels and at 3.4 eV in the spin-down channel, and at 4 eV in the spin-up channel, respectively. In both spin channels, the La-4f states contribute between the energies of 4.6 eV to 5.3 eV. For La1−xNdxAlO3 (at x = 50%), it is observed that the core and lower valence bands from −5.4 eV to −1.1 eV consist of mainly the Nd-4f states. Sharp peaks due to the Nd-4f states are observed at −1.6 eV and −1.2 eV in the spin-up configurations, respectively. At EF the sharp peak due to the Nd-4f state electrons is observed in the spin-up channel. Further peaks are also observed at 2.3 eV in the spin-down configuration, and at 2.4 eV in the spin-up configuration due to the Nd-4f state orbitals, respectively. Conversely, the La-4f state contributions are observed within an energy range from 3.5 eV to 4 eV with sharp peaks at 3.8 eV in both the spin up and spin down channels.

Fig. 3. (a) Total DOS plots of the La1−xNdxAlO3 alloys (0% < x < 100%); the partial DOS plots of the La-d, La-f, Al-p, O-s, and O-p states of the La1−xNdxAlO3 alloys at x = 0% (b), 25% (c), 50% (d), 75% (e), and 100% (f).
3.3. Band structure, energy band gap, and magnetic moment

Table 2 shows the variations of the direct and indirect band gaps of the La1−xNdxAlO3 alloys with concentration. The band gap is found to decrease with the increase of concentration. This is an indication of the fact that the band-gap of La1−xNdxAlO3 is tunable using the Nd ion in order to turn LaAlO3 into a promising candidate for optoelectronic applications. The plots of the concentration of doping with respect to band gap as displayed in Fig. 3(b) show a sharp decrease in the magnitude of the band gap for x = 0%, x = 25%, x = 50%, and x = 75%. As the concentration increases, the Nd-4f ions are found to contribute to the insulating[46] band gap of the undoped LaAlO3 as suggested by the density of states plots for the La1−xNdxAlO3 alloys as shown in Figs. 3(a)–3(e).

Table 2.

Fundamental direct and indirect band gaps of the La1−xNdxAlO3 alloys as compared with the previous results.

.

For La1−xNdxAlO3 (at x = 75%), the core and lower valence bands are found to be contributed by the Al-2p and O-2p state electrons with an energy of up to −1.0 eV. Both the Nd atoms (Nd-1 and Nd-2) are observed as contributors to the DOS in the valence region of the spin-up channel with peaks at −1.5 eV and EF (for Nd-2) respectively. In the spin-up configuration, contributions from the Nd-4f states are observed from 1.6 eV to 3.0 eV. The peaks at 1.7 eV in the spin-up channel and spin-down channel are due to both the Nd-4f states, where the peak at 1.9 eV in the spin-down channel is due to Nd-1. Conversely, the peaks at 2.3 eV are due to both Nd atoms in the spin-down channel and the peaks observed at 2.4 eV are due to the Nd1 atom in the spin-up channel. Strong hybridizations between both of these Nd-4f states are observed in both the valence region and the conduction region whereas the La-4f states are found to contribute from 3.4 eV to 3.9 eV in both spin-down channels. The DOS plots show that La1−xNdxAlO3 (at x = 75%) participates in maximum hybridization. At EF, the contributions of the Nd-4f states are observed in the spin-up configuration which indicates that this doping configuration is one of the important resulting systems compared with the remaining configurations. The splitting of the Nd-4f states could be attributed to the magnetic nature of the systems as suggested by the magnetic moments shown in Table 3.

Table 3.

Calculated spin magnetizations in units of μB of the bulk La1−xNdxAlO3 alloys and the supercells, on the basis of transition metal atom La and Nd. Note: Total moments presented are per structural unit cell. For x = 0% and 100%, one chemical formula unit is used which is equivalent to the structural unit cell of the bulk LaAlO3. For x = 50%, two chemical formula units were used, and for x = 25% and 75% four chemical formula units were used. The total energies and the moments for all doping rates with four chemical units were calculated and found to be consistent with the results presented in Table 1 and Table 3.

.

It is clearly seen from the figure that La1−xNdxAlO3 (0% < x < 100%) is a direct band gap material.[47] The substitution of the Nd atom does not affect the nature (direct band gap) of the compound but minimizes the gap as shown in Fig. 4(a). It is observed that for x = 50%, 75%, and 100% in La1−xNdxAlO3, the spin-down configuration is insulating whereas the mBJ-based electronic structure results clearly predict finite DOS at EF, for the spin-up configuration. Hence, these doped compounds are predicted to be half-metallic in nature.

Fig. 4. (a) Plots of direct and indirect band gap versus percentage of Nd doping in LaAlO3 and (b) plots of magnetic moment versus percentage of Nd doping.

In general the major contribution to the DOS of the La1−xNdxAlO3 (0% < x < 100%) alloys is due to the presence of the rare earth ion (Nd-4f) particularly near EF which has made this system an interesting candidate for doping studies. The direct band gap varies from 4.65 eV to 2.30 eV as shown in Table 2 and the indirect band gap varies from 4.65 eV to 2.00 eV with the doped Nd percentage in La1−xNdxAlO3 increasing from 0% to 100% as shown in Fig. 5.

Fig. 5. Calculated band structures of the La1−xNdxAlO3 alloys at x = 0% (a), 25% (b), 50% (c), 75% (d), and 100% (e) in the spin-up (black) and the spin-down (blue) channels.

The variations of the magnetic moment with concentrations are presented in Table 3 and Fig. 4(b). The non-magnetic LaAlO3 at x = 0% is found to exhibit magnetic ground state when doping with the Nd atoms. The sharp increases in the magnetic moment at x = 25%, 50%, and 75% and the magnetic nature of Nd can be attributed to the manifestation of the density of states at EF in the spin-up channel.

The band structures of the La1−xNdxAlO3 alloys at x = 0%, 25%, 50%, 75%, and 100% displayed in Figs. 5(a)–5(e) show that for the concentrations at x = 25%, 50%, and 75% the bands are more populated in the valence and conduction regions. The bands due to the La atoms are observed to be contributed in the conduction region and hence an insulating nature of LaAlO3 is observed. With the doping of the Nd-atom in Figs. 5(a)–5(d), both the spin-up (black) and the spin-down (blue) bands are plotted. In these cases, the spin-up and spin-down band structures are metallic and insulating, respectively, suggesting their possible applications for spintronic devices.

4. Conclusions

In this paper, the spinpolarized modified Becke–Johnson potential used to calculate the electronic properties of the La1−xNdxAlO3 alloys with different Nd concentrations (at x = 0%, 25%, 50%, 75%, and 100%). The observed electronic structures and the band features are explained each as a function of the concentration of the Nd-doped atom in LaAlO3 where the Nd-4f state exchange splitting originates from the magnetic nature of the system. With the band structures of the spin-up and spin-down configurations exhibiting metallic and insulating characteristics respectively, this system may be suitably designed for half metallic magnetic devices. Furthermore, the significant variation of band gap with doping concentration may be useful in important spintronic and opto–electronic applications.

Reference
1Sales B CGschneidner K AJrBunzli J C GPecharsky V KVasylechko LSenyshyn ABismayer U2003Handbook on the Physics and Chemistry of Rare EarthsAmsterdamElsevierChap. 242
2Islam M S2002Solid State Ionics154–15575
3Sangram K DBinod K R 2015 Chin. Phys. 24 067702
4Liu Y KYin Y WLi X G 2013 Chin. Phys. 22 087502
5Koren GGupta EGiess ASegmüller ALaibowitz R B 1989 Appl. Phys. Lett. 54 1054
6Zhang S BSun Y PZhao B CAng RZhu X BSong W H 2009 J. Alloys Compd. 479 22
7Henke MPerßon JKück S2000J. Lumin.87–891049
8Bahoura MMorris K JNoginov M A 2002 Opt. Commun. 201 405
9Maletic SMaletic DPetronijevic IDojcilovic JPopovic D M 2014 Chin. Phys. 23 026102
10Cho S YKim I THong K S 1999 J. Mater. Res. 14 114
11Huang CChen Y C 2002 Mater. Res. Bull. 37 563
12Yang PShi MQin SDeng H 2007 Mater. Lett. 61 2687
13Liu XLin J 2009 Solid State Sci. 11 2030
14Lybye DPoulsen F WMogensen M2009Solid State Ionics12891
15Yamasaka DTamagawa KOhki Y 2011 J. Appl. Phys. 110 074103
16Ge J JYang MXue X BYou BSun LZhang WWu X SHu ADu J 2012 Phys. Status Solidi 9 97
17Kuang X YZhou K W 2000 J. Phys. Chem. Solids 61 1225
18Wu GDeng HWang WZhang KCao HYang PChu J 2014 J. Mater. Sci.: Mater. Electron. 25 3137
19Liu H SFang X YSong W LHou Z LLu RYuan JCao M S 2009 Chin. Phys. Lett. 26 067101
20Cheng FYu Liu TZhang Q RQiao H LZhou X W 2011 Chin. Phys. Lett. 28 036106
21Lei S LLi BHuang JLi Q XYang J L 2013 Chin. Phys. Lett. 30 077502
22Hou Q YLi J JYing CZhao C WZhao E JZhang Y 2013 Chin. Phys. 22 077103
23Wang QLiang J FZhang R HLi QDai J F 2013 Chin. Phys. 22 057801
24Li S BYu H PZhang T1Chen ZWu Z M 2014 Chin. Phys. 23 107101
25Zylberberg JZuo-Guang Y 2006 J. Appl. Phys. 100 086102
26Murtaza GAhmad I 2012 J. Appl. Phys. 111 123116
27Namjoo SRozatian A S HJabbari IPuschnig P 2015 Phys. Rev. 91 205205
28Tran FBlaha P 2009 Phys. Rev. Lett. 102 226401
29Schwarz KBlaha P 2003 Comput. Mater. Sci. 28 259
30Sandeep Ghimire M PThapa R K 2011 J. Magn. Magn. Mater. 323 2883
31Blaha PSchwarz KMadsen G K HKvasnicka DLuitz J2001WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal PropertiesKarlheinz Schwarz, Techn. Universitat Wien Austria 3-9501031-1-2
32Wong K MAlay-e-Abbas S MFang YShaukat ALei Y 2013 J. Appl. Phys. 114 034901
33Sandeep Rai D PShankar AGhimire M PKhenata RThapa R K 2015 Phys. Scr. 90 065803
34Al-Sawai WLin HMarkiewicz R SWray L AXia YXu S YHasan M ZBansil 2010Phys. Rev. B821
35Guo S DLiu B G2010Europhys. Lett.9347006
36Meinert M2013Phys. Rev. B871
37Yousaf MSaeed M AAhmed RAlsardia M MIsa A R MShaari A 2012 Commun. Theor. Phys. 58 777
38Araujo R BDe Almeida J SFerreira Da Silva A 2013 J. Appl. Phys. 114 183702
39Perdew J PBurke KErnzerhof M 1996 Phys. Rev. Lett. 77 3865
40Sandeep RaiD PShankar AGhimire M PKhenata RThapa R K2016Mod. Phys. Lett. B301650028
41Wong K MAlay-e-Abbas S MShaukat AFang YLei Y 2013 J. Appl. Phys. 113 014304
42Murnaghan F D 1944 Proc. Natl. Acad. Sci. USA 30 244
43Boudali ASaadaoui FZemouli MDrissKhodja M DAmara K 2013 Adv. Mater. Phys. Chem. 3 146
44Bouvier PKreisel J 2002 J. Phys.: Condens. Matter 14 3981
45Luo XWang B 2008 J. Appl. Phys. 104 073518
46Ohtomo AHwang H Y 2004 Nature 427 423
47Lim S GKriventsov SJackson T NHaeni J HSchlom D GBalbashov A MUecker RReiche PFreeouf J LLucovsky G 2002 J. Appl. Phys. 91 4500
48Tang M JYang S QLiang T HYang Q XLiu K2013J. At. Mol. Sci.4280