† Corresponding author. E-mail:
Project supported by the National Key Basic Research and Technology Program, China (Grant No. 2010CB731601) and the National Natural Science Foundation of China (Grant No. 50871057).
Interactions between vacancies and Σ3 prismatic screw-rotation grain boundary in α-Al2O3 are investigated by the first principles projector-augmented wave method. It turns out that the vacancy formation energy decreases with reducing the distance between vacancy and grain boundary (GB) plane and reaches the minimum on the GB plane (at the atomic layer next to the GB) for an O (Al) vacancy. The O vacancy located on the GB plane can attract other vacancies nearby to form an O–O di-vacancy while the Al vacancy cannot. Moreover, the O–O di-vacancy can further attract other O vacancies to form a zigzag O vacancy chain on the GB plane, which may have an influence on the diffusion behavior of small atoms such as H and He along the GB plane of α-Al2O3.
Aluminum oxide, commonly referred to as alumina, is well known to have a broad technological significance. It is considered as a replacement gate oxide in the microelectronics industry, a substrate that is for growing the functional thin films, and as a support material for heterogeneous catalysts. Alumina has various allotropic forms of Al2O3, such as α-Al2O3, γ-Al2O3. Among the various allotropic forms, the stablest and well-characterized phase is α-Al2O3, which has a wide variety of technology applications such as high-temperature structure ceramics, dielectric insulators, and optical devices.
It was reported that the aluminum-rich coating with aluminum oxide is a very efficient hydrogen permeation barrier.[1–3] Moreover, both experimental and theoretical results showed that α-Al2O3 single crystal has a good resistance to hydrogen isotopic permeability.[4–6] Thus, α-Al2O3 has a potential application to the fusion reactor as a hydrogen isotopic permeation barrier in tritium production blankets to minimize tritium leakage. However, α-Al2O3 coatings, as a hydrogen isotopic permeation barrier, used in the engineering applications are often poly-crystalline. The presence of grain boundaries (GBs) and radiation-induced vacancies has a significant influence on the properties of α-Al2O3 coating against hydrogen isotopic permeation. It was reported that a rapid diffusion of oxygen along GBs via vacancies plays a crucial role in high temperature mechanical properties.[7–10] So far, it is still unclear whether there exists a rapid diffusion path along GBs via vacancies in α-Al2O3, which is crucial for the applications of α-Al2O3 coatings against hydrogen isotopic permeation. This motivates us to investigate the vacancy behavior near α-Al2O3 GBs.
Contrary to GBs, the formation energy of the point defect in perfect Al2O3 crystal has been systematically studied.[11–15] For instance, Xu et al.[16] studied the neutral and charged O vacancy in α-Al2O3 by supercell total-energy calculations using a first-principle method based on the density-functional theory. They obtained a theoretical zero-temperature O vacancy formation energy of 5.83 eV. However, the energetics of vacancies in α-Al2O3 GBs have not been well studied due to the fact that the atomistic structures of the GBs are complex. Recently, based on the fact that the atomic structure of pyramidal Σ13 twin GB has been characterized experimentally[17,18] and theoretically,[19] the defect energetics in pyramidal Σ13 twin GB of α-Al2O3 was investigated by Takahashi et al.[20] using a first principle projector-augmented wave method.
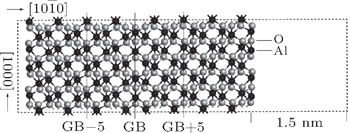
Apart from pyramidal Σ13 twin GB, the atomic structures of a few other GBs such as prismatic Σ3, basal Σ3, and rhombohedral Σ7 GBs have been characterized and proven to be periodic.[21–23] Among them, the prismatic Σ3 GB is special for its low GB energy and unique atomic layer structure, which consists of both Al and O atoms, in contrast to the other three GBs consisting of the atomic layers with either single Al or O atoms. From previous studies,[21] prismatic Σ3 GB has two possible structures: the screw-rotation twin and the glide-mirror twin. In the present study, we focus on the screw-rotation Σ3 twin GB with the lowest GB energy of 0.3 J/m2 among the alumina boundaries studied so far by the first-principle. Moreover, the atomic arrangement of prismatic Σ3 GB has been investigated by density functional theory and transmission electron microscopy.[21] It is proven that this GB is quite periodic and thus suitable for constructing the supercell with the realistic number of atoms.
In this study, a first-principle projector augmented wave (PAW) method is used to study the mono-vacancies, di-vacancies and vacancy–clusters at or near prismatic screw-rotation Σ3 GB. Vacancy formation energies, vacancy–vacancy, and vacancy–cluster binding energies are calculated to reveal vacancy–GB interactions in α-Al2O3. The model and simulation details are described in Section 2, followed by the results and discussion in Section 3, and conclusion in Section 4.
As shown in Fig. 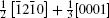
First principle calculations of prismatic Σ3 GB of α-Al2O3 were performed using a plane-wave-basis projector augmented wave(PAW) method[24] as implemented in the Vienna ab initio simulation package (VASP) code.[25–27] For the exchange correlation potential, the generalized gradient approximation (GGA)[28] was employed. In all the calculations, wave functions were expanded by plane waves with a maximum kinetic of 500 eV. The atoms, except for the outermost surface layers (fixed), were allowed to relax using a conjugate gradient scheme until their residual forces had converged to less than 0.01 eV/Å.
After optimizing the structure, we introduced a vacancy by removing an atom (Al or O) from different atomic layers away from GB and then calculated the vacancy formation energy. The GB system was treated neutrally without extra charges no matter whether vacancies were introduced. The vacancy formation energy is given by


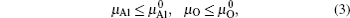
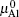

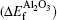

From Eqs. (

In order to obtain the range of μO, separate calculations of the total energies of fcc Al crystal and molecule O2 were performed. The encut kept the same throughout all the calculations, i.e., 500 eV. For metallic fcc-Al, a 14 × 14 × 14 Monkhorst–Pack mesh was used. In the case of oxygen, an isolated O2 molecule was placed in a 1.5 × 1.5 × 1.5-nm supercell, the calculation was performed with spin-polarized and 2 × 2 × 2k-point meshes.
An O vacancy may attract another O vacancy to form an O–O di-vacancy. Their binding ability was described by binding energy, Eb(VO1VO2), which is given by

Similarly, the binding energy, Eb(VAl), of an Al vacancy to a vacancy cluster VnO V(m−1) Al that contains nO vacancies and m − 1 Al vacancies, is determined as follows:

An O/Al vacancy is introduced by removing an O/Al atom from the relaxed structure as shown in Fig.
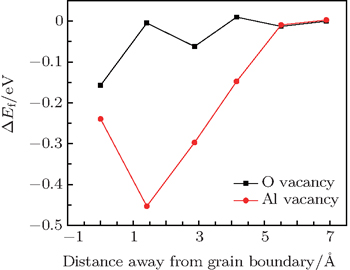
As a general tendency, it is often assumed that the Ef of vacancies near to the GB is smaller than those in the bulk-like region. As shown in Fig.
As is well known, di-vacancy configurations play an important role in vacancy aggregation into a large vacancy cluster in oxides. As discussed above, a mono-vacancy tends to migrate to GB areas, it is of interest to know whether a mono-vacancy located at the GB area would attract other vacancies to form a cluster in GB areas. One vacancy is chosen and fixed at the site with the lowest formation energy and another vacancy is varied and selected at different atomic layers. Figure
In the stoichiometric α-Al2O3, the concentration of O atoms is 1.5 times that of Al atoms. Moreover, as can be seen in Fig.
The O-vacancy chains consisting of O vacancies on or near the GB plane are the most possible form for vacancy clusters near the GB as shown in Fig.
A first principles calculation is performed to study the interactions between vacancies and prismatic Σ3 screw-rotation grain boundary in α-Al2O3. It turns out that the lowest vacancy formation energy for O (Al) vacancy occurs on the GB plane (the atomic layer next to the GB), suggesting that mono-vacancy tends to aggregate to GB areas. The O vacancies located on GB areas can attract other O vacancies nearby to form an O–O di-vacancy while Al vacancy cannot. The O–O di-vacancy can further attract other O vacancies to form a zigzag O vacancy chain on the GB plane, which is energetically favorable.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 |