Electrowetting refers to reducing the contact angle of droplets by applying a voltage between a droplet and a dielectric coated electrode, which has found numerous potential applications in lab-on-chip,^[1,2] optics,^[3,4] and displays.^[5–7] The contact angle change with voltage, described by the Young–Lippmann equation, predicts that the contact angle can be modulated to zero by increasing the voltage. However, the contact angle in fact reduces to a non-zero contact angle value beyond a critical external voltage, which deviates from the basic electrowetting theory, i.e., the Young–Lippmann equation. This phenomenon is widely known as contact angle saturation,^[8–12] which restricts the electrowetting-based applications.^[12–14]

In recent years, more and more investigations focused on exploring the underlying mechanisms responsible for contact angle saturation.^[12–16] Several debated hypotheses such as dielectric breakdown,^[11] zero interfacial tension,^[12] charge trapping,^[13] and air ionization^[14] have been proposed to ascertain this saturation phenomenon. Unfortunately, the physical origin of contact angle saturation is still poorly clarified, and the relevant theory that can directly predict the onset of the saturation and reducing the saturation of contact angle for a specific system, is scarce.

In this work, the physical origins of contact angle saturation are explored, and also a theoretical model is constructed to describe the variation of contact angle change with applied voltage at higher voltage. In the experiment, a 3-phase system consisting of different combinations of conductive fluid and oil is employed to measure the saturating contact angle response to the increasing voltage. We deduce that electrowetting saturation is dominated by the interfacial tension of the 3-phase system and the surface tension of conductive liquid. The saturating contact angle occurs once ions escape from the main droplet and form into small droplets. The relevant results will enrich the theory of electrowetting saturation and expand its application scope in electrowetting devices where an even larger range of contact angle modulation is desired.

Here we divide the electrowetting evolution into three stages: the first stage is that the change of cosine of the apparent contact angle (θ_v) with voltage can be well described by the Young–Lippmann equation,^[2] the second stage starts when the cosine of the contact angle deviates from the parabolic behavior predicted by the Young–Lippmann equation and ends when the contact angle ceases to respond to voltage, and the onset of the third stage corresponds to the point where the contact angle stops decreasing and keeps constant.

The classification criterion of the electrowetting evolution mentioned above mainly rests on the force analysis around the triple contact line and interface. When the applied voltage is low, the triple contact line is pinned and the local contact angle remains equal to Young angle θ_Y.^[16–18] The increase in electrostatic force tends to reduce the apparent angle θ_v while the local angle θ_Y keeps constant.^[18] The transition from the first stage to the second stage depends on the movement of the triple contact line, herein the potential point is defined as the first threshold potential (V_Th1). Beyond V_th1, the electrowetting force is strong enough to conquer the pinning force at triple phase contact line and drive the triple contact line into movement, accordingly the electrowetting evolves into the second-stage. In this stage, the oil viscous effect, oil resistance, and dynamic friction hinder the movement of triple contact line and result in the discrepancy between the electrowetting behavior and the Young–Lippmann equation.^[17] Keeping on increasing the voltage, the growing electrostatic force will eventually exceed the bonding force acting on the ions (or charges). The ions (or charges) start to escape from the main droplet once the interfacial tension can neither hold the ion(or charges) nor balance the electrowetting force,^[19] here the point of potential is called the second threshold voltage V_Th2. When V > V_Th2, the contact angle stops decreasing and the corresponding electrowetting evolution transfers from the second stage to the third stage.

According to the classification listed above, the Young–Lippmann equation is accurate to describe the first stage, and the contact angle keeps constant in the third stage. The following work mainly focuses on the second stage. A theoretical model is established to predict the variation of transient contact angle with higher potential for the second stage. Since the size of droplet is smaller than the capillary length (droplet volume is 0.5 μl), the surface tension has an influence on the droplet shape while the gravity is ignored.^[20] To simplify the problem, the droplet is considered to remain spherical in shape in the electrowetting process, which is illustrated in Fig. 1. Assume that the volume, side surface area, base surface, radius and height of droplet, and contact angle are V₀, A_s, A_b, R, R + h, and θ, respectively, where h = −Rcosθ, according to the calculation formulas of the volume and area for the spherical segment, then we will have the following relationships:

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Diagram of a droplet with radius R and contact angle θ.

Differentiating Eqs. (1)–(3), we can achieve the following equations:

Assuming that the droplet volume keeps constant, the differential equation of droplet volume equals zero, i.e., dV₀ = 0, and consequently

The changes of Helmholtz free energy from the side and base tension energy because of the droplet spreading, are

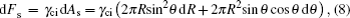
Here γ_ci, γ_cd, and γ_id denote the interfacial tension between conductive fluid and insulating fluid, conductive fluid and dielectric surface, and insulating fluid and dielectric surface, respectively.

When the potential V is applied to the electrowetting system, change of Helmholtz free energy induced by electrostatic energy is

Substituting Eq. (6) into Eq. (10), we can obtain

During the droplet spreading and contact line movement, the energy dissipation is dominated by the viscous effect, drag force, oil resistance, and dynamic friction around the triple contact line.^[21]

The viscous friction force and drag force of the moving contact line are linear with respect to the velocity of droplet edge movement^[17,21]

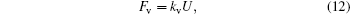
Here, n ∼ 10 is the logarithm of macroscopic length over microscopic length, and α is a constant. For simplicity, equation (14) is rewritten as

The components of energy dissipation caused by the viscous effect, oil resistance and dynamic friction are shown as^[22]

The total change of Helmholtz free energy is expressed as

The electrowetting system satisfies the Helmholtz free energy minimization once it reaches equilibrium, one can have

Substituting Eqs. (7), (8), (9), (11), (14a), and (15) into Eq. (17) yields

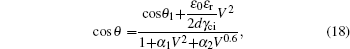
The relation for the whole electrowetting evolution is shown below

The threshold voltages V_Th1 and V_Th2 in Eq. (19) can be theoretically derived based on our theories listed above. When V = V_Th1, the electrowetting force F_el is larger than the sum of the maximum static friction force F_p and capillary force F_cap, and then triggers the triple contact line moving.^[16] Consequently

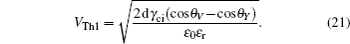
When voltage increases to V_Th2, the electrowetting force value F_el = ε₀ε_r/2dV² starts to exceed the capillary force F_cap = γ_ci(cosθ_v−cosθ_Y), the surface tension γ of the conducting fluid and static friction forces. Before the contact line moves and contact angle decreases, the ions start to break the fluid bondage because of the lower interfacial energy, escape from main drop and then lead to electrowetting saturation. By eliminating the static friction force F_P, we can have

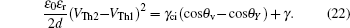
Rearranging Eq. (22) leads to

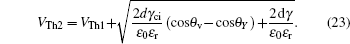
A series of experiments is implemented to verify the validity of the proposed theoretical model. The photos of electrowetting are shown in Fig. 2, and also the diagrams of the basic electrowetting testing setup are shown in the inset of Fig. 2. The complete substrates coated with parylene C (d = 3.6 μm, ε_r = 3.15) and CYTOP (∼ 50 nm thickness) are placed in a clear acrylic box and immersed in an insulating fluid. The conductive fluids are deposited with a pipette (drop 0.5 μl) and electrically biased through the insertion of a tungsten probe tip (10 μm in diameter) connected to a Trek power amplifier (model 603) coupled to a Tektronix AFG 3022B function generator. The contact angle change is monitored and measured with drop shape analysis systems (software version 2.0), which are repeated 3 times at fresh sample locations.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Diagrams and photos of electrowetting at (a) 0 V and (b) 180 V.

The insulating fluid and the conductive fluid employed in Fig. 2 are isopar oil with surface tension γ_isopar = 27 mN/m and propylene glycol with surface tension γ = 35 mN/m), respectively, and the interfacial tension between propylene glycol and isopar oil is γ_ci = 9.957 mN/m. Figure 2 shows that the correlated initial contact angle θ_Y is about 156° and the final saturating contact angle approaches to ˜15°. When V ≥ 150 V, the saturating contact angle occurs, which is characterized by many micro-jet satellite droplets accumulating around the main droplet instead of dielectric breakdown.

Figure 3 shows the variations of measured contact angle with voltage (◼: experimental data) and their comparisons with the results predicted by the Young–Lippmann equation (●: Young–Lippmann equation) and our theoretical model Eq. (19) (▲: theoretical model). Since the Young–Lippmann equation ignores the energy dissipation during the droplet spreading, it starts to deviate from the experimental data curve at the point voltage V = 37.5 V and decreases to zero sharply. As a matter of fact, the contact angle observed in the experiment continues to decrease slowly when V ≥ 37.5 V and eventually keeps constant when voltage V ≥ 150 V. Our theoretical curve predicts the evolution of the transient contact angle in electrowetting, which shows good consistence with the relevant experimental results. They show that the contact angle decreases sharply in the beginning, and then declines slowly during the second stage, and finally it evolves into the saturation state. In Fig. 3, the point potentials V₁ = 37.5 V and V₂ = 150 V correspond to the first and second threshold potential V_Th1 and V_Th2 respectively in our theory, which are calculated via Eqs. (21) and (23). Substituting γ_ci = 9.957 mN/m, d = 3.6 μm, F_el = 2ηγ_ci, ε₀ = 8.85 × 10⁻¹², ε_r = 3.15, θ_Y = 156°, V = 37.5 V, and θ_v = 117° into Eq. (21), we obtain the first theoretical threshold potential V_Th1 = 34.5 V. Employing Eq. (23), the second theoretical threshold potential V_Th2 = 117.9+V_Th1 = 152.4 V is calculated at V = 150 V and θ_v = 15° by the following parameters: γ_ci = 9.957 mN/m, d = 3.6 μm, ε₀ = 8.85 × 10⁻¹², ε_r = 3.15, γ = 35 mN/m, V_Th1 = 34.5 V, and θ_Y = 156°. Obviously, our theoretical threshold potentials V_Th1 = 34.5 V and V_Th2 = 152.4 V are in good agreement with the experimental values V₁ = 37.5 V and V₂ = 150 V, respectively.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Comparison of plot of contact angle versus applied voltage among experimental data (◼), results from Young–Lippmann equation (●), and theoretical data (▴).

To elucidate the influences of interfacial and surface tension on electrowetting behavior more clearly, different combinations of conductive and insulating fluids with the same conductivity are employed for the test, and the results are shown in Fig. 4. The insulating fluids include a blend of Dow Corning OS silicone oils (80 wt% OS-20, 10 wt% OS-10, and 10 wt% OS-30, γ_silicone = 21 mN/m) and a hydrocarbon blend (Isopar M, C11–C16 isoalkanes with <2% aromatics, γ_Isopar = 27 mN/m), while the conductive fluids include propylene glycol (TBA-Ac, 5% black Pigment, γ_PG = 35 mN/m) and DI water (γ_DI = 73 mN/m). From Fig. 4, we can find that the conductive fluid dominates the saturating contact angle size and the onset of electrowetting saturation while the influence of insulating fluid on electrowetting saturation is negligible. It is also remarkable that good system stability performance, as shown by the small error bar, is achieved by employing propylene glycol as the conductive fluid.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Plots of contact angle versus applied voltage for different combinations of conductive and insulating fluid.

Figure 5 shows the discrepancies in the saturating contact angle among different surface tensions of conductive fluid in isopar oil, where conductive fluid and isopar oil have the same conductivity. It again confirms that the magnitude of the saturating contact angle increases with the surface tension of conductive fluid, and the minimum saturating contact angle is about 25° for pure propylene glycol (PG) while that of DI water is around 50°, which is attributed to the difference of surface tension between the different conductive fluids. According to surface free energy theory, to reduce the contact angle, electrostatic force is required to overcome ion binding energy and then drive a certain number of internal ions (or charges) to the surface of the droplet.^[25] Hence, it implies that the smaller the surface tension of the conductive fluid, the smaller the electrostatic energy consumed by one ion (or charge) migrating from inside to the interfacial surface. Since the surface tension of propylene glycol (γ ∼ 35 mN/m) is smaller than that of DI water (γ ∼ 73 mN/m), much more internal ions (or charges) in PG are driven to the surface under the same applied voltage, and consequently a lower saturating contact angle is achieved.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Plots of contact angle versus voltage for different volume percentages of DI water in PG, where DI water and PG have the same conductivity 16.8 μS.

Figure 5 also shows that the smaller the interfacial tension of the 3-phase system, the earlier the onset of the saturating contact angle is. It can be found in Figs. 4 and 5 that compared with pure DI water, the conductive fluid comprised pure PG reaches the contact angle saturation earlier, i.e., V_th2,PG < V_th2,water, which is in agreement with the results of Chevalliot et al.^[26] Since the interfacial tension of PG and insulating fluid (γ_ci,PG = 9.957 mN/m) is smaller than that of DI water and insulating fluid (γ_ci,water = 43 mN/m), the corresponding interface binding energy, the energy that one escaping ion in PG needs to overcome, is smaller. When the applied voltage is increased to a certain value, the electrostatic energy is powerful enough to drive the ions in PG into migrating to the interface and escaping from the main droplet while inner ions in DI water are still bound tightly. Therefore, it seems to be reasonable to conclude that saturation is triggered when ions are pulled from the main droplet and it is dominated by the interfacial tension, which is consistent with Liu et al.’s results.^[25]

This work focuses on the exploration of the physical origin of electrowetting saturation, approaches to lowering the saturating contact angle, and the construction of a theoretical model for calculating the threshold potential and describing electrowetting behavior. Proper combination of the 3-phase system employed succeeds in dropping the saturating contact angle below 25° and achieving a good system stability performance. The theoretical model established to predict the transient contact angle change with higher potential shows good agreement with the relevant experiments. As for the electrowetting saturation, it is triggered once ions (or charges) escape through the interface of the droplet. A 3-phase system with higher interfacial tension and lower surface tension of conductive liquid facilitates to generate the lower contact angle and delay the formation of electrowetting saturation. The relevant results will enrich the research of electrowetting, promote the application in the area of micro-optics and opto-electronic information technology, and thus expand its application scope.