Cite this Article
Zhang Qing-Yu, Sun Dong-Ke, Zhang You-Fa, Zhu Ming-Fang. Numerical modeling of condensate droplet on superhydrophobic nanoarrays using the lattice Boltzmann method. Chinese Physics B, 2016, 25(6): 066401  
Permissions
Numerical modeling of condensate droplet on superhydrophobic nanoarrays using the lattice Boltzmann method
Zhang Qing-Yu1, Sun Dong-Ke2, 3, Zhang You-Fa1, Zhu Ming-Fang1, †,
Jiangsu Key Laboratory for Advanced Metallic Materials, School of Materials Science and Engineering, Southeast University, Nanjing 211189, China
Department of Mechanical Engineering Technology, Purdue University, 401 North Grant Street, West Lafayette, IN 47907, USA
Shanghai Key Laboratory of Advanced High-Temperature Materials and Precision Forming, Shanghai Jiao Tong University, Shanghai 200240, China

 

† Corresponding author. E-mail: zhumf@seu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 51101035, 51371051, and 51306037).

Abstract
Abstract

In the present study, the process of droplet condensation on superhydrophobic nanoarrays is simulated using a multi-component multi-phase lattice Boltzmann model. The results indicate that three typical nucleation modes of condensate droplets are produced by changing the geometrical parameters of nanoarrays. Droplets nucleated at the top (top-nucleation mode), or in the upside interpillar space of nanoarrays (side-nucleation mode), generate the non-wetting Cassie state, whereas the ones nucleated at the bottom corners between the nanoarrays (bottom-nucleation mode) present the wetting Wenzel state. Time evolutions of droplet pressures at the upside and downside of the liquid phase are analyzed to understand the wetting behaviors of the droplets condensed from different nucleation modes. The phenomena of droplet condensation on nanoarrays patterned with different hydrophilic and hydrophobic regions are simulated, indicating that the nucleation mode of condensate droplets can also be manipulated by modifying the local intrinsic wettability of nanoarray surface. The simulation results are compared well with the experimental observations reported in the literature.

PACS: 64.70.fm;82.70.Uv;05.50.+q;47.61.Fg
Keyword:condensate droplet;superhydrophobic nanoarray;wettability;lattice Boltzmann method
1. Introduction

A droplet deposited at the top of superhydrophobic nanoarrays may present the non-wetting Cassie state with an apparent contact angle larger than 150°.[1] However, the wetting states of condensation-induced droplets can change when the superhydrophobic nanoarrays are exposed to humid air. This is because small condensation-induced droplets might nucleate and grow everywhere on the rough surface and hence degenerate the superhydrophobicity,[2,3] which influences the antifogging,[4] anti-icing,[5] and heat transfer efficiency[6] of the rough surfaces drastically. For investigating the evolution of the condensate droplets on superhydrophobic nanoarrays, researchers performed in-situ observations of the condensation process using environmental scanning electron microscopy (ESEM).[7,8] However, owing to heating effects of the electron beam and other unpredictable factors,[9,10] the resolution of ESEM is usually on a submicrometer scale, whereas the critical size of the condensation-induced droplet nucleus is on a nanoscale. As a result, people could only observe the final wetting states of the large droplets rather than the whole condensation process involving droplet nucleation.[11–13]

With the rapid development of computational technology, numerous numerical efforts have been made to study the wetting behavior of droplets on superhydrophobic surface.[14–17] In recent years, the lattice Boltzmann method (LBM) has rapidly developed into a powerful numerical approach and has been used in many fields.[18–26] The LBM has also attracted a lot of attention in the simulations of wettability of the nanoarray surface due to its simplicity and efficiency.[27–30] It is noted that most numerical activities using the lattice Boltzmann (LB) model have primarily been performed through placing a droplet on a micro- or nano-structured surface to investigate the wetting behavior, where the process of droplet nucleation was not involved. The numerical study of droplet nucleation using the LBM has so far remained scarce compared with the modeling of wetting behavior of artificially positioned droplets. As is well known, however, a better understanding of the nucleation process of condensate droplet is crucial to studying the final wetting state of droplets on superhydrophobic nanoarrays. Fu et al.[31] adopted a single-component multi-phase LB model to simulate droplet condensations on surfaces with different structures. It is found that the nucleation behavior depends on the spacing between and height of ridges on superhydrophobic surface. However, the structure with hydrophilic surface has little effect on the condensation. The present authors[32] employed a multi-component multi-phase pseudopotential LB model to simulate the droplet nucleation and growth on superhydrophobic nanoarrays. Three typical preferential nucleation modes of condensate droplets are observed through LB simulations with various geometrical parameters of nanoarrays, which are found to affect the wetting properties of nanostructured surfaces significantly. Since the nanostructures were regularly arranged, the droplet nucleation and growth took place uniformly on the nanoarray surfaces, producing the non-realistic droplet patterns, i.e., uniform liquid films, rather than individual liquid droplets.

In the present study, further simulations of the condensation process are carried out using the multi-component multi-phase pseudopotential LB model. The geometrical parameters and the local intrinsic wettabilities of nanoarrays are adjusted to be nonhomogeneous to investigate their influences on the preferential nucleation sites and the growth patterns of condensate droplets. The final wetting states of droplets simulated by the LB model are compared with the experimental observations reported in the literature.[33–36]

2. Model description and domain configuration

In the two-dimensional (2D) multi-component multi-phase pseudopotential LB model,[37] two sets of distribution functions are implemented for the two fluid components, namely, H2O and other non-H2O gases. The processes of particle propagation and collision are governed by the LB equations using the 2D nine-velocity (D2Q9) scheme as the following

where is the density distribution function of the σ-th component, τσ and Δt are the relaxation time and the time-step, respectively, and ei are the discrete velocities in the D2Q9 scheme and given by

where c = Δx/Δt is the lattice speed, and Δx is the lattice spacing. The equilibrium distribution function, , is expressed as

where the weight coefficients ωi are taken as ω0 =4/9, ω1−4 = 1/9, and ω5−8 = 1/36; ρσ is the macroscopic density of the σ-th component given by . The macroscopic velocity uσ(x,t) is calculated by uσ(x,t) = u′(x,t) + τσFσ(x,t)/ρσ, where u′(x,t) is the composite macroscopic velocity calculated through

and Fσ(x,t) is the force acting on the σ-th component, which includes the fluid–fluid cohesion force and the fluid–solid adhesion force .

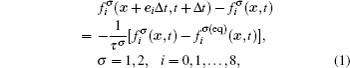
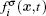
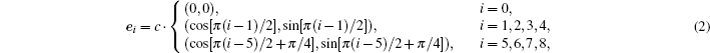
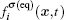
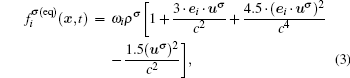
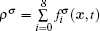
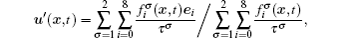
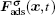
The fluid–fluid cohesive force acting on the σ-th component is defined as

where σ and denote the two different fluid components, Gc is the fluid–fluid interaction strength that controls the cohesion force, ψσ(x,t) and are the pseudo-potentials that are taken as fluid densities, i.e., ψσ(x,t) = ρσ(x,t) and in the present work. The pressures at different positions are calculated by the equation of state as follows:

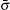
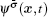
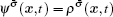
The fluid–solid adhesion force acting on the σ-th component is computed as

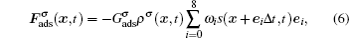
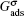
where s(x + eiΔt,t) is an indicator function that is equal to 1 or 0 for a solid or a fluid component node, respectively. The interaction strength between the fluid and solid phases can be adjusted by . It is suggested that values are positive for non-wetting fluids and negative for wetting fluids, respectively.

In the present work, periodic boundaries are employed on the left and right walls of the computation domain. A bounce-back rule is adopted on the fluid/solid boundaries. A constant density boundary condition, implemented by the non-equilibrium extrapolation approach,[38] is used on the top boundary as an air source. The densities of gaseous water and non-H2O gas components inside the domain are initialized to be 0.04 mu lu−2 and 0.96 mu lu−2 (mass unit per square lattice unit), while those on the top boundary are fixed to be 0.08 mu lu−2 and 0.92 mu lu−2, respectively. The humid air with higher gaseous water concentration on the top boundary enters into the computation domain and the gaseous water accumulates around the arranged solid nanoarrays due to the adhesive force. Droplet nucleation takes place around the nanoarrays once supersaturation has been achieved.

3. Results and discussion
3.1. The intrinsic contact angle

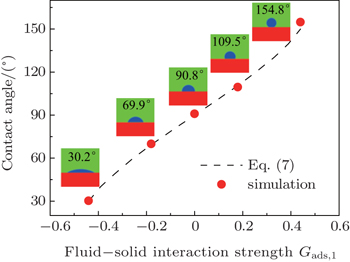
Different intrinsic contact angles of a droplet on smooth surfaces with different wettabilities are simulated. The simulation domain consists of 200 × 200 lattice units. A droplet with a radius of 26 lattice units is positioned on the flat surface. The relaxation time is set as τ = 1 for the two components. The fluid–fluid interaction strength is fixed as Gc = 2.1. 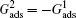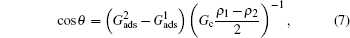The fluid–solid interaction strengths are specified as , which is identical to the work of Huang et al.[39] Substituting the interaction parameters into Young’s equation, a rearrangement of Young’s equation yields[39]

where θ is the intrinsic contact angle, ρ1 is the water component density in the droplet, and ρ2 is the dissolved non-H2O gas component density in the droplet.[39] Figure 1 shows the comparison between the contact angles obtained from the LB simulations and the calculations from Eq. (7). As shown in the figure, the simulated intrinsic contact angles are in good agreement with the computed data, and the relative error between the two sets of data is less than 3.2%. This indicates that various wetting phenomena of the gas/liquid/solid system can be reasonably described by the present LB model. Moreover, it is worthwhile to mention that the dynamic contact angles of droplets, exhibiting the hysteresis effect, can also be simulated by the present LB model.

Fig. 1. Comparison between the LB simulations and the calculations from Eq. (7) for the intrinsic contact angle as a function of the fluid–solid interaction strength.
3.2. Nucleation and growth of condensate droplets

The phenomena of the nucleation and subsequent growth of condensate droplets are simulated using the LB model. To reasonably compare the LB simulations with the experimental observations, the relationship between the dimensionless LB lattice and the realistic length space is established through evaluating the critical nucleation diameters of condensate droplets. Under the experimental condition of 6 Torr (1 Torr = 1.33322 × 102 Pa) and 3 °C,[33–35] the critical nucleation diameter is 60 nm calculated by Kelvin’s equation.[40] In the LB model the critical nucleation diameter is measured to be 3 lattice units. Accordingly, it is obtained that 1 lattice unit in the LB model is equivalent to 20 nm in the real length space.[32] In addition, the fluid–solid interaction strengths are taken as to produce a 109° intrinsic contact angle that determines a coincident surface energy with those of the rough surfaces used in the droplet condensation experiments.[33–35] In the computation domain, the geometrical parameters of nanoarrays include post width (W), edge-to-edge spacing between two adjacent posts (S), and post height (H).

In our previous work,[32] three types of typical preferential nucleation positions, i.e., top-nucleation, side-nucleation, and bottom-nucleation modes were observed. The relationship between the geometrical parameters of nanoarrays and the preferential nucleation position was determined based on the exactly regular nanoarray arrangements. Considering that in experiments there must be some levels of nonhomogeneity in the geometrical size of the nanostructures in the present work, the patterns of the superhydrophobic nanoarrays are regulated to be nonuniform in the present work, i.e., they have slight differences in post width, post height, and inter-post spacing at some sites to test the influences of geometrical parameters on the preferential position of droplet nucleation.

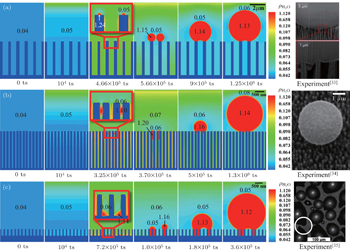
Three types of droplet nucleations and the subsequent growths are presented in Fig. 2 that is shown in water density field. Figure 2(a) shows the evolution of droplet nucleation and growth in the case of the top-nucleation mode. The computational domain is composed of 324 × 500 lattice units. The geometrical parameters are taken as W = 16 lattice units (320 nm), S = 38 lattice units (760 nm), and H = 220 lattice units (4400 nm). The two center posts are set to be slightly taller and thicker. After starting the LB calculation, water density in the gas phase gradually increases from the initial value of 0.04 mu lu−2 due to the constant humid air source with 0.08 mu lu−2 at the top boundary. After around 4.66 × 105 time-steps of the LB calculation, two droplet nuclei appear at the top of the middle posts as shown in the third panel of Fig. 2(a). A water density gradient at the surrounding atmosphere is formed due to the consumption of the gaseous water particles as the droplets grow. As the vapor condensation proceeds, the growing droplets coalesce and lie at the top of nanoarrays without penetrating into the space between posts, keeping a non-wetting Cassie state and exhibiting a good agreement with the experimental observation shown in the last panel of Fig. 2(a).[33]

Figure 2(b) shows the simulated evolution of the side-nucleation mode, illustrating a transition from the wetting Wenzel state to the non-wetting Cassie state of condensate droplets. The simulation domain consists of 124 × 220 lattice units. The geometrical parameters are W = 5 lattice units (100 nm), S = 4 lattice units (80 nm), and H = 100 lattice units (2000 nm), while the middle four posts and the interpillar space are a little taller and narrower, respectively. Other simulation conditions are identical to those of Fig. 2(a). It is found that the droplet nucleation takes place in the upside of the narrower interpillar space between the nanoarrays. Then, the condensate liquid coalesces to a larger droplet and the liquid in the space moves upwards gradually. Finally, the condensate droplet remaining at the top of the nanoarrays in the non-wetting Cassie state compared well with the ESEM image[34] shown in the last panel of Fig. 2(b).

Figure 2(c) shows the simulated evolution of the bottom-nucleation mode. The simulation is performed in a domain of 153 × 200 lattice units. The geometrical parameters of the nanoarrays are W = 4 lattice units (80 nm), S = 8 lattice units (160 nm), and H = 21 lattice units (420 nm), but the middle region has a slight difference in post height and inter-post spacing. Other modeling conditions are identical to those of Figs. 2(a) and 2(b). It is noted that droplets emerge in the bottom corners of the narrower spacings. These droplets grow and coalesce into a single droplet, keeping pinning in the space between the posts. Apparently, this feature would impair the superhydrophobic property of nanoarrays. The image of condensate multidroplets taken by Chen et al.[35] is presented in the last panel of Fig. 2(c) for comparison. The elongated shape of the white circled droplet in the last panel of Fig. 2(c) exhibits a large contact angle hysteresis, presenting good agreement with the simulation results.

It is noted that the simulation results presented in Fig. 2 are corresponding to the relationship between the geometrical parameters of nanoarrays and nucleation modes, which was established in our previous work using the exactly uniform nanoarray arrangements.[32] This demonstrates that the nucleation mode will not be changed because geometrical configurations of nanoarrays are exactly uniform nor slightly nonuniform. However, the slightly nonuniform geometrical configurations can produce realistic individual condensate droplets that are comparable to those observed experimentally.

Fig. 2. Simulated evolutions of droplet condensation shown in water (H2O) density field, for the cases: (a) top-nucleation mode, (b) side-nucleation mode, and (c) bottom-nucleation mode. Numbers in the figures indicate the local water (H2O) densities.

To illustrate the mechanism that drives the motion of the interpillar droplets growing from the side-nucleation mode, time evolutions of liquid pressures taken from the locations close to the upside and downside liquid/gas or liquid/solid interfaces of Figs. 2(b) and 2(c) are shown in Fig. 3. As shown in Fig. 3(a), for the droplets originating from the side-nucleation mode the downside pressure is higher than the upside pressure during the period from 3.95 × 105 ts (time steps) to 5.75 × 105 ts, which drives the liquid in the interpillar space to move upwards until the condensate droplet is entirely sitting at the top of the nanoarrays. However, figure 3(b) shows that for the droplets originating from the bottom-nucleation mode the downside pressure is always markedly lower than the upside pressure. Consequently, the condensate droplets are not able to move upwards during condensation, resulting in the wetting Wenzel state in the entire process of droplet nucleation and growth.

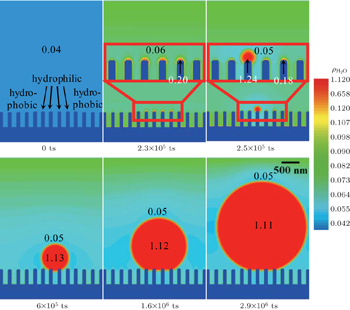
Fig. 3. Evolutions of the upside and downside pressures of the liquid phase measured from (a) Fig. 2(b) and (b) Fig. 2(c). The unit muts is short for mass unit per time step.
Fig. 4. Simulated evolution of droplet condensation on nanoarrays patterned with hydrophilic and hydrophobic surfaces, shown in water (H2O) density field. The geometrical parameters of the nanoarrays are identical to those of Fig. 2(c). Numbers indicate the local water (H2O) densities.

To investigate the influence of nonuniform local intrinsic wettability on the preferential nucleation mode of condensate droplets, the simulation is carried out using the nanostructures of Fig. 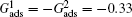2(c), but decorated with different hydrophilic and hydrophobic surfaces as shown in the first panel of Fig. 4. The top surfaces of four posts in the middle region are decorated to be hydrophilic by setting to generate an intrinsic contact angle of 50°. Other simulation conditions are identical to those of Fig. 2(c). Figure 4 presents the time evolution of the droplet condensation on the nanoarrays patterned with hydrophilic and hydrophobic regions. It is found that the gaseous water particles favourably accumulate at the hydrophilic tops of the four posts as the condensation proceeds, as shown in the second panel of Fig. 4. After around 2.5 × 105 time steps of LB calculation, the droplet nucleus appears on one of the hydrophilic tops after reaching supersaturation for droplet nucleation. The droplet grows by consuming the gaseous water particles, producing a water density gradient at the surrounding atmosphere. In the process of LB simulation, the droplet stays at the top of the nanoarrays and remains a non-wetting Cassie state, which can be readily removed from the surface. Note that the final wetting state of the condensate droplet completely differs from that shown in Fig. 2(c), even though both figures 2(c) and 4 have the exactly identical geometrical parameters. This indicates that the modification of local intrinsic wettability on nanoarrays can change the nucleation mode and the subsequent growth pattern of the condensate droplets. The simulation results in Fig. 4 accord with the experimental observations by Varanasi et al.[36] qualitatively.

4. Conclusions

Droplet nucleation and growth on nanoarrays are simulated using a 2D multi-component multi-phase LB model. Different intrinsic contact angles are simulated using various fluid–solid interaction strengths. By changing the geometrical parameters of the nanoarrays, three types of preferential droplet nucleation modes are observed. It is confirmed that the condensate droplets originating from the top-nucleation and side-nucleation modes display the non-wetting Cassie state, while the ones growing from the bottom-nucleation mode present the wetting Wenzel state. The slightly nonuniform geometrical configurations of nanoarrays can generate realistic individual condensate droplets. The simulation results compare reasonably well with the experimental observations reported in the literature.

The simulated time evolutions of droplet pressures show that the downside pressure of the droplet originating from side-nucleation mode is slightly higher than the upside pressure, which drives the droplets to move upwards until a non-wetting Cassie state is reached. However, the downside pressure of the droplet originating from bottom-nucleation mode is always lower than the upside pressure in the entire condensation process, which keeps the droplets in the wetting Wenzel state. The hydrophilic/hydrophobic modification of the local intrinsic wettability on the nanoarray surface can change the preferential droplet nucleation positions from the bottom-nucleation mode to the top-nucleation mode. It is demonstrated that the patterns of droplet condensation can be manipulated by controlling the geometrical parameters of nanoarrays, and the local intrinsic wettabilities on nanoarray surfaces.

Reference
1Lafuma AQuere D 2003 Nat. Mater. 2 457
2Dorrer CRuehe J 2007 Langmuir 23 3820
3Narhe R DBeysens D A 2006 Europhys. Lett. 75 98
4Park K CChoi H JChang C HCohen R EMckinley G HBarbastathis G 2012 ACS Nano 6 3789
5Guo PZheng YWen MSong CLin YJiang L 2012 Adv. Mater. 24 2642
6Peng BMa XLan ZXu WWen R 2015 Int. J. Heat Mass Transfer 83 27
7Zhang Y FWu HYu X QChen FWu J 2012 J. Bionic Eng. 9 84
8Rykaczewski KPaxson A TAnand SChen X MWang Z KVaranasit K K 2013 Langmuir 29 881
9Rykaczewski KScott J H JFedorov A G 2011 Appl. Phys. Lett. 98 093106
10Royall C PThiel B LDonald A M 2001 J. Microsc. 204 185
11Rykaczewski K 2012 Langmuir 28 7720
12Warsinger D E MSwaminathan JMaswadeh L ALienhard J H 2015 J. Membr. Sci. 492 578
13Hou YYu MChen XWang ZYao S 2015 ACS Nano 9 71
14Farhangi M MGraham P JChoudhury N RDolatabadi A 2012 Langmuir 28 1290
15Liu Y WMen Y MZhang X R 2012 J. Chem. Phys. 137 204701
16Guo Q MLiu Y WJiang G FZhang X R 2014 Soft Matter 10 1182
17Wang YChen S 2015 Appl. Surf. Sci. 327 159
18Zhang C BDeng Z LChen Y P 2014 Int. J. Heat Mass Transfer 70 322
19Zhang WWang YQian Y H 2015 Chin. Phys. 24 064701
20Sun D KXiang NJiang DChen KYi HNi Z H 2013 Chin. Phys. 22 114704
21Meng X HGuo Z L 2015 Phys. Rev. 92 043305
22Zhou X YCheng BShi B C 2008 Chin. Phys. 17 238
23Liang HChai Z HShi B CGuo Z LZhang T 2014 Phys. Rev. 90 063311
24Esfahanian VDehdashti EDehrouye-Semnani A M 2014 Chin. Phys. 23 084702
25Xu A GZhang G CYing Y J2015Acta Phys. Sin.64184701(in Chinese)
26Chen RShao J GZheng Y QYu H DXu Y S 2013 Commun. Theor. Phys. 59 370
27Kusumaatmaja HYeomans J M 2007 Langmuir 23 6019
28Gross MVarnik FRaabe DSteinbach I2010Phys. Rev. E81051606
29Zhang J FKwok D Y 2006 Langmuir 22 4998
30Zhang BWang J JZhang X R 2013 Langmuir 29 6652
31Fu X WYao Z HHao P F 2014 Langmuir 30 14048
32Zhang Q YSun D KZhang Y FZhu M F 2014 Langmuir 30 12559
33Rykaczewski KLandin TWalker M LScott J H JVaranasi K K 2012 ACS Nano 6 9326
34Lau K KBico JTeo K BChhowalla MAmaratunga G AMilne W IMckinley G HGleason K K 2003 Nano Lett. 3 1701
35Chen C HCai QTsai CChen C LXiong GYu YRen Z 2007 Appl. Phys. Lett. 90 173108
36Varanasi K KHsu MBhate NYang WDeng T 2009 Appl. Phys. Lett. 95 094101
37Shan XDoolen G 1995 J. Stat. Phys. 81 379
38Guo Z LZheng C GShi B C 2002 Chin. Phys. 11 366
39Huang H BThorne D TSchaap M GSukop M C 2007 Phys. Rev. 76 066701
40Li S LZhou Y PLiu J J2010Physical ChemistryBeijingHigher education Press471(in Chinese)